setor 1215

setor 1215
12150509
12150509-SP
Aula 35
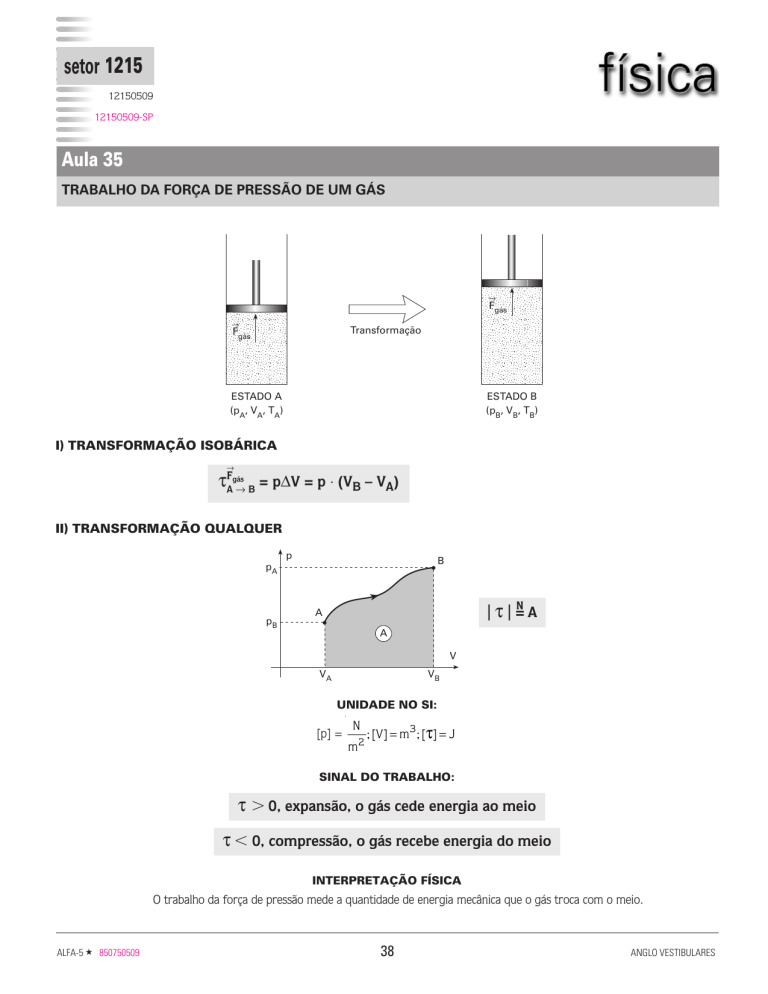
TRABALHO DA FORÇA DE PRESSÃO DE UM GÁS
→
Fgás
→
Transformação
Fgás
ESTADO A
(pA, VA, TA)
ESTADO B
(pB, VB, TB)
I) TRANSFORMAÇÃO ISOBÁRICA
→
Fgás
τA → B = pΔV = p ⋅ (VB – VA)
II) TRANSFORMAÇÃO QUALQUER
p
B
pA
pB
| τ | =N A
A
A
V
VA
VB
UNIDADE NO SI:
[p] =
N
m2
; [ V ] = m 3 ; [ τ] = J
SINAL DO TRABALHO:
τ 0, expansão, o gás cede energia ao meio
τ 0, compressão, o gás recebe energia do meio
INTERPRETAÇÃO FÍSICA
O trabalho da força de pressão mede a quantidade de energia mecânica que o gás troca com o meio.
ALFA-5 ★ 850750509
38
ANGLO VESTIBULARES
b) Calcule o trabalho realizado pela força de pressão do
gás nas transformações A → B → C.
Exercício
A → B: isobárica:
1. Um mol de um gás ideal, inicialmente no estado A com temperatura 300 K, é submetido a uma sequência de transformações A → B → C indicado no diagrama V versus T a
seguir.
V (m3)
B
0,3
τA → B = pΔV = 2,4 ⋅ 104 ⋅ (0,3 – 0,1) = 4,8 ⋅ 103 J
B → C: isométrica:
τB → C = 0 ∴ τtotal = 4,8 ⋅ 103 J
C
0,2
0,1
A
T (K)
0
300
600
900
1200
Adote R = 8 J/mol ⋅ K.
a) Represente a sequência de transformações A → B → C
no diagrama pressão × volume.
3,2 × 104
2,4 × 104
p (N/m2)
C
B
A
1,6 × 104
0,8 × 104
ORIENTAÇÃO DE ESTUDO
V(m3)
0,1
0,2
0,3
Livro 3 — Unidade I
A: pAVA = nRTA
pA ⋅ 0,1 = 1 ⋅ 8 ⋅ 300 ⇒ pA
Caderno de Exercícios — Unidade IX
= 2,4 ⋅ 104 N/m2
Tarefa Mínima
B: pBVB = nRTB
•
•
pB ⋅ 0,3 = 1 ⋅ 8 ⋅ 900 ⇒ pB = 2,4 ⋅ 104 N/m2
Leia os itens 1 e 2, cap. 7.
Resolva os exercícios 15, 16 e 17, série 2.
C: pCVC = nRTC
pC ⋅ 0,3 = 1 ⋅ 8 ⋅ 1200 ⇒ pC = 3,2 ⋅ 104 N/m2
Tarefa Complementar
•
ALFA-5 ★ 850750509
39
Resolva os exercícios 19 a 23, série 2.
ANGLO VESTIBULARES
Aula 36
PRIMEIRA LEI DA TERMODINÂMICA
UM GÁS É SUBMETIDO A UMA TRANSFORMAÇÃO
Exercícios
1. Um gás, em contato com um corpo quente, recebe 50J de
energia. Simultaneamente, o gás sofre uma expansão e o
trabalho realizado pela força de pressão do gás, em módulo,
é 70J. Determine a variação de energia interna do gás.
transformação
O gás ganhou 50 J de calor: Q = +50 J
O trabalho de força de pressão na expansão é 70J:
τ = + 70 J.
1ª- lei da termodinâmica: ΔU = Q – τ
ΔU = 50 – 70
ΔU = – 20 J
(ESTADO B)
(pB; VB; TB)
(ESTADO A)
(pA; VA; TA)
• Qualquer transformação gasosa ocorre com trocas de
energia entre o gás e o meio.
• As trocas de energia podem se dar por dois mecanismos
distintos:
a) troca de energia térmica (medida pela quantidade de
calor Q).
b) troca de energia mecânica (medida pelo trabalho da
força de pressão do gás τ).
2. Certa massa de gás ideal transfere 200 J de energia térmica para uma fonte fria.
Durante esse processo, o gás foi submetido a uma compressão, em que o trabalho de força de pressão do gás foi,
em módulo, 150 J.
Qual foi a variação de energia interna desse gás?
• Pelo princípio da conservação de energia, a diferença
entre as quantidades trocadas de energia pelos dois
mecanismos corresponde à variação de energia interna.
Em símbolos: ΔU = Q – τ
(Método 1)
Sem avaliação de sinal
trabalho na
compressão
INTERPRETANDO OS SINAIS
150J
ΔU: variação de energia interna.
ΔU 0 ⇒ o gás esquenta (T aumenta).
ΔU 0 ⇒ o gás esfria (T diminui).
Gás
ΔU = – 50J
Q: quantidade de calor trocado.
Q 0: o gás recebe calor do meio.
Q 0: o gás cede calor ao meio.
(Método 2)
Com avaliação do sinal
• o gás perde calor: Q = – 200J
τ: trabalho da força de pressão do gás.
τ 0: expansão → o gás cede energia ao meio.
τ 0: compressão → o gás recebe energia do meio.
• trabalho na compressão: τ = – 150J
ΔU = Q – τ
• 1ª- lei:
ΔU = – 200 – (– 150)
ΔU = – 50 J
LEMBRANDO:
3
2
ou
5
Δ U = nR Δ T
2
calor 200J
Δ U = nR Δ T (gás monoatômico)
ALFA-5 ★ 850750509
(gás diatômico)
40
ANGLO VESTIBULARES
3. Assinale certo (C) ou errado (E) nas sentenças a seguir.
a) ( E ) Um gás somente pode ser aquecido por calor.
b) ( E ) Quando um gás recebe calor, certamente, sua temperatura se eleva.
c) ( C ) É possível aquecer um gás sem que lhe seja fornecido calor.
d) ( E ) A equação ΔU = Q – τ se aplica somente a sistemas
gasosos.
e) ( C ) Um gás pode sofrer uma transformação sem que
ocorra variação de energia interna.
ORIENTAÇÃO DE ESTUDO
Livro 3 — Unidade I
Caderno de Exercícios — Unidade IX
Tarefa Mínima
Leia os itens 1 a 4, cap. 6.
Resolva os exercícios 26 e 27, série 2.
•
Resolva os exercícios 29 e 30, série 2.
Tarefa Complementar
a) ( E ) Um gás pode ser aquecido, por exemplo, por
compressão.
b) ( E ) Ele pode ser resfriado, se a perda de energia
mecânica for maior que o ganho de calor.
d) ( E ) Essa equação é válida p/ qualquer sistema.
ALFA-5 ★ 850750509
•
•
41
ANGLO VESTIBULARES
Aulas 37 e 38
TRANSFORMAÇÕES GASOSAS
Diagrama p × V
Transformações
p
Isotérmica
(T é constante)
Equações
hipérbole
pA
• 1ª- Lei da Termodinâmica
ΔU = 0
A
∴ Q=τ
| τ|
ΔU = 0
T' T
T
B
pB
VB
VA
V
p
Isobárica
(p é constante)
B
A
p
T' T
• 1ª- Lei da Termodinâmica
ΔU = Q – τ
ΔU = m ⋅ cp ⋅ ΔT – pΔV
|τ|
cp é o calor específico do gás
à pressão constante.
T
VB
VA
V
p
Isométrica
(V é constante)
τ=0
• 1ª Lei da Termodinâmica
ΔU = Q, pois τ = 0
B
pB
A
pA
cV é o calor específico do gás
a volume constante.
T
V
ALFA-5 ★ 850750509
ΔU = m ⋅ cV ⋅ ΔT
T' T
V
42
ANGLO VESTIBULARES
Diagrama p × V
Transformações
Equações
• 1ª- Lei da Termodinâmica
p
pA
ΔU = – τ
A
Expansão adiabática:
o gás esfria.
Adiabática
(Q = 0)
|τ|
pB
VA
B
T
V
VB
p
Cíclica
(Tf = Ti)
Compressão adiabática:
o gás esquenta.
T' T
• 1ª- Lei da Termodinâmica
ΔU = 0
∴
| τ|
p
T' T
Q=τ
• ciclo no sentido horário: τ 0
• ciclo no sentido anti-horário: τ 0
T
V
V
2. (UFPR-adaptada) Considere um cilindro de paredes termicamente isoladas, com exceção da base inferior, que é condutora de calor. O cilindro está munido de um êmbolo de
área 0,01 m2 e peso 25 N, que pode mover-se sem atrito.
O êmbolo separa o cilindro em uma parte superior, onde
existe vácuo, e uma parte inferior, onde há um gás ideal,
com 0,01mol e volume inicial de 10 litros. À medida que
o gás é aquecido, o êmbolo sobe, muito lentamente, até
uma altura máxima de 0,1 m, onde um limitador de curso
o impede de subir mais. Em seguida, o aquecimento prossegue até que a pressão do gás duplique.
Exercícios
1. Assinale certo (C) ou errado (E) nas sentenças a seguir.
a) ( C ) Em qualquer transformação gasosa, ocorrem trocas de energia entre o gás e o meio exterior.
b) ( C ) Na transformação isométrica, o gás somente pode
ser aquecido por calor.
c) ( C ) Na expansão adiabática, a variação de energia interna é negativa.
d) ( E ) Na expansão isobárica, o gás diminui sua temperatura.
e) ( E ) Em uma transformação isotérmica, o gás não troca
calor com o meio.
f) ( E ) Na transformação cíclica, o trabalho total da força
de pressão é nula.
Adote: R = 8
J
mol ⋅ K
isolamento
térmico
d) ( E ) pV = nRT (p, n e R)
são constantes na isobárica. Logo, na expansão (aumento de V) ocorre um aumento na T.
limitador
de curso
vácuo
h = 0,1 m
êmbolo
e) ( E ) Isotérmica ⇒ ΔU = 0
gás
∴ Q=τ
f) ( E ) Cíclica ⇒ ΔU = 0
chama
∴ τciclo = | Qrec – Qced |
ALFA-5 ★ 850750509
43
ANGLO VESTIBULARES
f) Certo. Só houve trabalho durante a expansão. A transformação pode ser representada pelo diagrama:
Com base nessas informações, assinale certo (C) ou errado (E).
a) ( C ) Enquanto o êmbolo estiver subindo, o processo é
isobárico.
b) ( E ) Após o êmbolo ter atingido o limitador, o processo é
adiabático.
c) ( C ) O trabalho realizado pela força do gás no trecho de
expansão do gás é de 2,5J.
d) ( E ) A temperatura no instante inicial é igual a 402K.
e) ( C ) O calor fornecido ao gás, na etapa de expansão, é
utilizado para realizar trabalho e para aumentar a
temperatura do gás.
f) ( C ) O trabalho realizado pelo gás durante a etapa de
expansão é igual ao trabalho total realizado pelo gás
desde o início do aquecimento até o momento em
que o gás atinge o dobro da pressão inicial.
p
(f)
2p
p
(i)
τ
10
11
Comentário:
a) Certo. A pressão exercida pelo gás no êmbolo é praticamente igual à pressão devida ao peso do êmbolo, uma
vez que o êmbolo “sobe muito lentamente”, ou seja, a resultante é praticamente nula.
b) Errado. O gás continua recebendo calor da fonte térmica.
ORIENTAÇÃO DE ESTUDO
c) Certo. Sendo uma transformação isobárica, o trabalho é
dado por.
τ = p ⋅ ΔV =
Livro 3 — Unidade I
Caderno de Exercícios — Unidade IX
P
⋅ (A ⋅ h)
A
Tarefa Mínima
τ = P ⋅ h = 25 ⋅ 0,1
τ = 2,5 J
AULA 37
•
•
d) Errado. pV = nRT
25
⋅ 10 ⋅ 10 –3 = 0,01 ⋅ 8 ⋅ T
0,01
AULA 38
•
•
T = 312,5 K
e) Certo. Houve um aumento na temperatura, pois na transformação isobárica, V e T são diretamente proporcionais.
Como V aumentou, T aumentou. Logo, a energia proveniente da fonte térmica foi utilizada para a realização de
trabalho (aumento de energia potencial gravitacional do
êmbolo) e aumento na agitação das partículas (aumento
da energia cinética total do gás).
ALFA-5 ★ 850750509
Leia os itens 3 e 4, cap. 7.
Resolva os exercícios 31 a 34, série 2.
Leia os itens 5 e 6, cap. 7.
Resolva os exercícios 35 e 36, série 2.
Tarefa Complementar
AULA 37
•
Resolva os exercícios 37 e 38, série 2.
AULA 38
•
44
Resolva os exercícios 39 a 42, série 2.
ANGLO VESTIBULARES
Aulas 39 e 40
SISTEMA MASSA/MOLA E PÊNDULO
Segue então:
OSCILADORES HARMÔNICOS
Os movimentos harmônicos simples (MHS) apresentam as
seguintes características.
T=
• O corpo em MHS repete seu estado cinemático (mesma
posição, mesmo vetor velocidade e mesmo vetor aceleração) em intervalos de tempo iguais, denominados período (T).
• O corpo realiza um movimento de vai-e-vem em uma trajetória que é um segmento de reta ou, pelo menos, muito
próximo de um segmento de reta.
• A resultante das forças que atuam no corpo tem comportamento análogo ao da força elástica. Portanto, sua intensidade pode ser escrita como R = (const) ⋅ |x|, em que
x representa a posição do corpo. Dizemos que a resultante se comporta como uma força restauradora, isto é,
ela sempre aponta para a posição de equilíbrio.
SISTEMA MASSA / MOLA
K
A
A
(m)
— Equilíbrio
posição de
equilíbrio
K
m
Há dois osciladores harmônicos que apresentam interesse
ao nosso estudo:
• sistema massa/mola.
• pêndulo simples.
–A
K
T = 2π
0
posição de
equilíbrio
1 k
2π m
m
• PERÍODO (T) é o intervalo de tempo necessário para que
o corpo realize uma oscilação completa.
Em outras palavras, é o menor intervalo de tempo para que
o estado cinemático do corpo se repita.
No sistema internacional: [T] = s
PÊNDULO SIMPLES
θ
g
• FREQUÊNCIA (f) é o número de oscilações realizadas pelo
corpo por unidade de tempo.
número de oscilações
Δt
No sistema internacional: [ f ] =
1 –1
= s = Hz (hertz)
s
0
Pequenas oscilações (θ 5°)
Das definições acima, pode-se montar a seguinte relação:
ALFA-5 ★ 850750509
f=
0
• AMPLITUDE (A) é a distância entre a posição central da
trajetória até qualquer uma das posições dos extremos da
trajetória.
intervalo de tempo
T
1
m
k
+A
GRANDEZAS ASSOCIADAS ÀS OSCILAÇÕES
f=
1
1
ou f =
f
T
———
———
número de oscilações
1
f
T = 2π
45
g
f=
1 g
2π ANGLO VESTIBULARES
Com relação a essa montagem, assinale certo (C) ou errado
(E) para as afirmações a seguir.
I. ( C ) Se esse pêndulo for levado para a Lua, seu período de oscilação irá aumentar.
II. ( E ) Se trocarmos o corpo por outro de massa 4m, a
frequência desse pêndulo irá duplicar.
III. ( C ) Se duplicarmos o comprimento do fio, o período
do pêndulo aumentará, aproximadamente, 41%.
IV. ( E ) Caso esse sistema seja empregado como um relógio, este irá se atrasar à medida que L diminuir.
Exercícios
1. Um corpo de pequenas dimensões e massa M se encontra
preso a uma mola ideal de constante elástica K. A partir de
certo instante, o corpo é retirado de sua posição de equilíbrio, passando a realizar oscilações harmônicas de amplitude
A, período T e frequência f.
K
A
A
II. Errado. A frequência e o período de um pêndulo só dependem do comprimento L do fio (ou haste) e do campo
gravitacional local (g).
L
IV. Errado. Como T = 2π
, o aumento de L acarreta um
g
m
aumento em T. Se o período de oscilação aumenta; o
relógio irá se atrasar.
Com relação a essa montagem, assinale certo (C) ou errado
(E) nas afirmações a seguir.
I. ( E ) As oscilações ocorrem em torno da posição livre
da mola.
II. ( E ) Se a amplitude de oscilação for reduzida à metade, o período de oscilação também será reduzido
à metade.
III. ( E ) Se a massa do corpo fosse aumentada, a frequência de oscilação também aumentaria.
IV. ( E ) Se esse sistema fosse levado à Lua, o período de
oscilação diminuiria.
V. ( C ) A intensidade da velocidade do corpo é máxima
quando este passa pela posição de equilíbrio desse
sistema.
ORIENTAÇÃO DE ESTUDO
Livro 3 — Unidade III
Caderno de Exercícios — Unidade X
Tarefa Mínima
AULA 39
I. As oscilações se dão em torno da posição de equilíbrio.
II. O período de oscilação do sistema massa/mola não
depende da amplitude.
III. Se a massa aumentar, a frequência diminuirá.
IV. O período do sistema massa/mola não depende da
aceleração gravitacional.
•
•
Leia os itens 1 a 3, do texto “os osciladores harmônicos” que está
após a Tarefa Complementar.
Resolva os exercícios 2, 3 e 4, série 1.
AULA 40
•
•
2. Um corpo de pequenas dimensões e massa m é preso a um
fio leve e inextensível, cujo comprimento é L. A seguir, o
corpo é retirado da posição de equilíbrio e abandonado, passando a realizar oscilações harmônicas de período T e frequência f. Considere que o campo gravitacional na região
tenha intensidade g.
Leia os itens 4 e 5 do texto “Os osciladores harmônicos”.
Resolva os exercícios 17 e 18, série 1.
Tarefa Complementar
AULA 39
•
Resolva os exercícios 5, 6 e 7, série 1.
AULA 40
•
→
g
Resolva os exercícios 19 e 20, série 1.
LEITURA COMPLEMENTAR
()
OS OSCILADORES HARMÔNICOS
1. INTRODUÇÃO
Não é incomum observarmos alguns corpos cujos movimentos
apresentam a característica de serem repetitivos (periódicos). Por exemplo, quando o motor de um automóvel mantém sua rotação constante, o
cilindro dentro do pistão executa o movimento de vai-e-vem em intervalos de tempos iguais.
(m)
–A
ALFA-5 ★ 850750509
0
+A
46
ANGLO VESTIBULARES
O movimento da Terra ao redor do Sol é outro exemplo de um
movimento periódico. A posição da Terra em relação ao Sol se repete
em intervalos de tempos iguais. Uma boia disposta em um ponto de
um líquido, percorrido por ondulações regulares, realiza oscilações
periódicas.
A
A
Fe
x
0
x=A
Fe
x
Terra
0
x
Sol
x
0
Fe
x
0
Fe
Dentre os movimentos periódicos, passaremos a analisar, nessas
aulas, aqueles cuja trajetória é um segmento de reta ou, pelo menos,
muito próximo de um segmento de reta. Em especial, há dois movimentos de interesse imediato: oscilação de corpo preso a uma mola
ideal e a oscilação de um pêndulo simples.
x
x = –A
0
Fe
x
0
Por conveniência, a trajetória é orientada para a direita e a posição
de equilíbrio (posição central da oscilação) é tomada como sendo o
marco zero. A localização do corpo é dada pela abscissa x.
A amplitude A de oscilação é definida como a distância entre
qualquer um dos extremos da trajetória até a posição central da oscilação. O período de oscilação T é definido como sendo o menor intervalo de tempo para que o corpo ocupe a mesma posição, com o mesmo vetor velocidade. De forma simplificada, período é o intervalo de
tempo necessário para que o corpo realize uma oscilação completa.
Exceção feita à posição central da trajetória, onde a resultante é
nula, repare que, durante a oscilação, a resultante das forças que atuam
sobre o corpo durante a oscilação coincide com a força elástica.
Em símbolos:
Felást = R
Ou seja:
R=K⋅X
Na expressão acima, “X” representa a deformação da mola, contada a partir da posição livre da mola. Como a posição livre da mola
coincide com a posição central da trajetória, a deformação X assume
valores iguais ao módulo da abscissa x.
Quando um corpo realiza oscilações em trajetórias retilíneas, em
que a resultante das forças que atuam sobre ele apresenta comportamento análogo ao da força elástica, dizemos que o corpo realiza um
movimento harmônico simples (MHS). Dizer que a resultante apresenta comportamento análogo ao da força elástica significa que a resultante tem intensidade que é diretamente proporcional ao módulo da
abscissa (x) que localiza o corpo na trajetória.
2. O SISTEMA MASSA / MOLA
Considere um corpo de massa m, apoiado sobre um piso horizontal e sem atrito, preso a uma mola ideal de constante elástica K.
N
O
3. O PERÍODO DE OSCILAÇÃO
DO SISTEMA MASSA/MOLA
P
Quando analisamos detalhadamente as oscilações de um corpo
preso a uma mola ideal, é possível demonstrar que o período de oscilação desse sistema é dado por.
Inicialmente, na posição indicada na figura, a mola não está comprimida, nem esticada e, por consequência, a força elástica é nula. Como
a força peso P é equilibrada pela força de contato (força normal N), nessa
posição, a resultante das forças no corpo é nula. Resumindo, essa é a posição de equilíbrio (0). A seguir, o corpo é retirado dessa posição e abandonado, passando a realizar oscilações periódicas em torno de 0.
ALFA-5 ★ 850750509
⎛ m⎞
T = 2π ⎜ ⎟
⎝K⎠
47
ANGLO VESTIBULARES
Caso haja um profundo interesse em se conhecer o “caminho” percorrido até a obtenção da equação acima, sugerimos que o aluno leia o
texto Movimento Harmônico Simples, itens 1 a 7, unidade III, cap. 1.
θ
Comentários acerca da equação do período de oscilação do sistema
massa/mola
1) Demonstra-se que a equação acima é válida para qualquer direção que
o corpo oscile. Em outras palavras, o período de oscilação do sistema
massa/mola não depende da direção que ocorrem as oscilações.
(1)
x
0
A trajetória é orientada para direita e a posição de equilíbrio (posição central da oscilação) é tomada como o marco zero. As posições do
corpo são indicadas pela abscissa x.
2) Observando as variáveis contidas na equação acima, podemos concluir que:
a) O período de oscilação do sistema massa mola não depende da
amplitude de oscilação.
b) O período de oscilação do sistema massa mola não depende da
aceleração gravitacional (g) local.
c) O período de oscilação do sistema massa mola só depende:
— da massa oscilante (m)
— da constante elástica da mola (K).
x
3) Como a frequência é dada por
f=
1
,
T
Tomemos uma posição desse corpo, em que sua abscissa é x.
Por conveniência, x 0. Uma vez que a trajetória é aproximada para
um segmento de reta, podemos considerar que a resultante R das
forças que atuam no corpo é horizontal e sempre aponta para a posição de equilíbrio 0.
a frequência do sistema massa mola é:
⎛ 1 ⎞ ⎛K⎞
f=⎜ ⎟ ⎜ ⎟
⎝ 2π ⎠ ⎝ m ⎠
Obs. Os comentários feitos com relação ao período também são
válidos para a frequência.
θ
4. O PÊNDULO
Suponha um corpo de dimensões desprezíveis, de massa m e
preso a um fio inextensível e leve, de comprimento L. A outra extremidade do fio é presa a um suporte horizontal e o sistema pode oscilar
livremente, sem a ação de forças dissipativas.
Na posição de equilíbrio, a força peso atuante no corpo é equilibrada pela força de tração que o fio exerce no corpo
P θ
T
R
T
R
0
x
No triângulo maior em destaque:
senθ =
T
x
L
No triângulo menor em destaque:
tg θ =
P
R
P
Uma vez que estamos analisando os casos em que θ 10°, o
valor do seno de θ e de tangente de θ são praticamente idênticos.
(Somente para se ter uma idéia; sen 10° ≈ 0,174 e tg 10° ≈ 0,176).
Assim sendo, é bastante razoável estabelecer a seguinte igualdade:
x R
=
L P
A seguir, o sistema é retirado do equilíbrio e abandonado a partir da
posição 1, passando a realizar oscilações em torno da posição de equilíbrio. Vamos considerar que o ângulo (θ), formado entre a vertical que
passa pelo ponto de suspensão do fio e a reta que une o corpo na posição
1 e o ponto de suspensão seja inferior a 10°. Verifica-se que, nessa circunstância, a trajetória é praticamente um segmento de reta e a oscilação
do corpo, como veremos a seguir, pode ser considerada um MHS.
ALFA-5 ★ 850750509
P
48
ANGLO VESTIBULARES
2) Analisando essa equação, conclui-se que o período de oscilação de
um pêndulo oscilando com pequenas amplitudes só depende:
a) do comprimento (L) do pêndulo,
b) da aceleração gravitacional (g) do local onde se encontra o pêndulo.
3) O período de oscilação de um pêndulo simples não depende:
a) do valor da massa oscilante (m),
b) da amplitude (A) de oscilação (desde que o ângulo de oscilação
seja inferior a 10°)
4) Como a frequência é dada por
1
f= ,
T
Note que P e L são constantes. Logo, a equação acima pode ser
escrita como:
R = (const.) ⋅ x
Ou seja, a resultante é diretamente proporcional ao módulo da abscissa. Em outras palavras, ela apresenta comportamento análogo ao da
força elástica.
Concluindo: se considerarmos um pêndulo com pequenas oscilações, o corpo realiza um MHS.
5. PERÍODO DE OSCILAÇÃO DE UM PÊNDULO
É possível demonstrar que o período T de oscilação de um pêndulo simples vibrando com pequenas oscilações (θ 10°) é dado por
a frequência de oscilação do pêndulo é:
⎛ 1 ⎞ ⎛ g⎞
f=⎜ ⎟ ⎜ ⎟
⎝ 2π ⎠ ⎝ L ⎠
⎛ L⎞
T = 2π ⎜ ⎟
⎝ g⎠
Obs. Os comentários feitos a respeito do período também são válidos para a frequência.
Novamente, caso haja um profundo interesse em conhecer as
passagens que levaram à equação acima, sugerimos ler os textos da
página 106, do livro 3.
5) Suponha que um relógio tenha seu mecanismo de contagem de
tempo com base na oscilação de um pêndulo. Considere que o
relógio funcione corretamente quando o período de oscilação for T.
a) Caso o período de oscilação desse relógio passe a ser T’, tal
que T’ T, o relógio irá se atrasar.
b) Caso o período de oscilação desse relógio passe a ser T’, tal
que T’ T, o relógio irá se adiantar.
Comentários acerca da equação do período de oscilação de um pêndulo
simples
1) A equação acima somente é válida nos casos em que o pêndulo
realiza pequenas oscilações.
ALFA-5 ★ 850750509
49
ANGLO VESTIBULARES