Guia de aula
2. Luz e matéria
2.1. Ondas (revisão)
Ondas. O movimento causado por uma perturbação que se propaga através de um meio.
É a propagação de energia de um ponto a outro sem que haja transporte de matéria entre
eles.
Exemplo
• Colocando-se um pedaço de cortiça na água, próximo ao local do lançamento
da pedra, verifica-se que a onda, ao atingir a cortiça que fica flutuando na
superfície da água, faz com que ela apenas oscile, subindo e descendo, sem
variar a direcção.
• Como a rolha não é arrastada, concluímos que a onda não transporta matéria.
Porém, como ela se movimenta, implica que recebeu energia da onda.
Tipos de ondas
Quanto à natureza:
Ondas mecânicas: são aquelas que precisam de um meio material para se
propagar (não se propagam no vácuo). Geradas por vibrações.
Exemplo: Ondas em cordas e ondas sonoras (som).
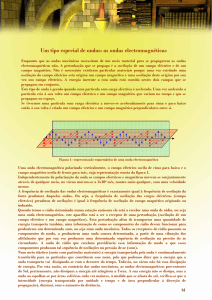
Ondas electromagnéticas: são geradas por cargas eléctricas aceleradas ou/e
oscilantes e não necessitam de uma meio material para se propagar, podendo se
propagar no vácuo.
Exemplos: Ondas de rádio, de televisão, de luz, raios X, raios laser, ondas de
radar etc.
1
Quanto à direcção de vibração
Transversais: são aquelas cujas vibrações são perpendiculares à direcção de
propagação.
Exemplo: Ondas em corda.
Longitudinais: são aquelas cujas vibrações coincidem com a direcção de
propagação.
Exemplos: Ondas sonoras, ondas em molas.
.
Ondas transversais
Ondas longitudinais
Som
2
Ondas periódicas
São ondas geradas por fontes de energia que executam oscilações periódicas.
Ondas periódicas
A forma da onda permanece constante e se desloca para a direita
É uma onda sinusoidal porque a forma é da função seno
Propriedades da onda periódica:
•
•
•
•
•
Comprimento de onda – distância entre dois máximos consecutivos.
Frequência – número de ciclos por segundo (Hz) (quantos picos passam num
determinado ponto num segundo)
Amplitude – deslocamento máximo de um ponto da onda.
Período – tempo que a onda leva para fazer uma oscilação.
Velocidade – v
T
3
Princípio da Sobreposição
Quando duas ou mais ondas se propagam, simultaneamente, num mesmo meio, diz-se
que há uma sobreposição de ondas.
4
Ondas Estacionárias
São ondas resultantes da sobreposição de duas ondas de mesma frequência, mesma
amplitude, mesmo comprimento de onda, mesma direcção e sentidos opostos.
2.2. Equações de Maxwell
As ondas electromagnéticas permeiam o nosso ambiente. Na forma de luz visível
podemos ver o mundo com os nossos olhos. Ondas infravermelhas da superfície da terra
aquecem o ambiente. Microondas cozinham o nosso alimento e também são usadas nos
sistemas de comunicação de radar. As ondas de radiofrequência transmitem os nossos
programas de rádio favoritos.
Origem das ondas electromagnéticas: carga eléctrica acelerada.
As ondas mecânicas, como o som necessitam de um meio material para se propagarem,
enquanto que as ondas electromagnéticas podem se propagar no vácuo.
5
As leis fundamentais do electromagnetismo, as equações de Maxwell (escocês),
são a base de todos os fenómenos electromagnéticos. A partir dessa generalização
Maxwell forneceu uma importante ligação entre campos eléctricos e magnéticos.
Através dessas equações ele previu a existência das ondas electromagnéticas. Que se
deslocam no vácuo à velocidade da luz c 1 0 0 = 300 000 m/s. Esta descoberta
levou a várias aplicações práticas, como o rádio e a televisão, e também a constatação
de que a luz é uma forma de radiação electromagnética.
As quatro equações de Maxwell aplicadas ao vácuo são:
1ª Equação.
Q
E
dA
0
É a lei de Gauss, e estabelece que o fluxo eléctrico total através de qualquer superfície
fechada é igual à carga líquida contida dentro dessa superfície, dividida por 0 . Essa lei
descreve como as cargas criam campos eléctricos. As linhas do campo eléctrico têm
origem nas cargas positivas e terminam nas cargas negativas.
2ª Equação.
B
dA 0
Esta equação é considerada a Lei de Gauss para o magnetismo. Ela diz que o fluxo
magnético através de uma superfície fechada é nulo. O número de linhas de campo
magnético que entram num volume fechado é igual ao número de linhas que deixam o
volume. Isso implica que as linhas de campo não podem começar e terminar em algum
ponto. Significa que não existem monopólos magnéticos e de facto não são observados
monopólos magnéticos isolados na natureza (norte e sul separados).
3ª Equação.
E ds
d B
dt
É a Lei de Faraday, que descreve como um campo magnético variável cria um campo
eléctrico. A integral de linha do campo eléctrico em torno de qualquer trajectória
fechada é igual à taxa de variação do fluxo magnético através de qualquer superfície
limitada por essa trajectória.
4ª Equação.
d E
B
ds 0 I 0 0 dt
É uma forma generalizada da lei de Ampère e descreve como uma corrente eléctrica ou
um campo eléctrico variáveis criam um campo magnético. A integral de linha do campo
magnético em torno de qualquer trajectória fechada é determinada pela corrente
resultante e pela taxa de variação do fluxo eléctrico através de qualquer superfície
limitada por essa trajectória.
Se os campos eléctricos e magnéticos são conhecidos em algum ponto do espaço, a
força que esses campos exercem sobre uma partícula de carga q é calculada por:
F qE qv B
6
Chamada Força de Lorentz.
Uma descrição completa de todas as interacções electromagnéticas clássicas é dada
pelas equações de Maxwell e pela força de Lorentz.
2.3. Ondas Electromagnéticas
A teoria unificada do electromagnetismo de Maxwell (1831 – 1879) demonstrou que
campos eléctricos e magnéticos dependentes do tempo, satisfazem uma equação
semelhante as ondas acústicas, as quais obedeciam a uma equação diferencial
denominada equação de onda:
2 y( x, t ) 1 2 y( x, t )
2
x 2
v
t 2
São derivadas parciais porque a função de onda y ( x, t ) (é uma onda progressiva) e
depende de duas variáveis, x, t.
A teoria de Maxwell prevê a existência das ondas electromagnéticas. Esta onda
electromagnética consiste de campos eléctricos oscilantes. Um campo eléctrico variável
induz um campo magnético e um campo magnético variável induz um campo eléctrico.
A partir das equações de Maxwell obtemos as equações:
2 B ( x, t ) 1 2 B ( x, t )
2
x 2
c
t 2
ou
2 E ( x, t ) 1 2 E ( x, t )
2
x 2
c
t 2
As soluções mais simples para essas duas equações são:
E Emáx coskx t
e B Bmáx coskx t
onde Emáx e Bmáx são os valores máximos dos campos, k 2 o número de onda,
, o comprimento de onda e 2f , a frequência angular.
Se substituirmos as soluções acima nas equações de onda, podemos relacionar os
campos eléctricos e magnéticos da seguinte forma:
Emáx
c
Bmáx
e
E
c
B
Em qualquer instante a razão entre o campo eléctrico e o campo magnético de uma onda
electromagnética é igual à velocidade da luz.
Em 1888, Heinrich Hertz, físico alemão, foi o primeiro que gerou e detectou ondas
electromagnéticas em laboratório.
7
Propagação da onda electromagnética
A energia transportada por uma onda electromagnética é descrita pelo vector S ,
chamado vector de Poynting:
1
S
EB
0
Existem diversas formas de ondas electromagnéticas que se diferenciam pelas suas
frequências e comprimentos de ondas.
Espectro das ondas electromagnéticas
8
Ondas de rádio. Resultam de cargas aceleradas, por exemplo através de fios
condutores de uma antena de rádio. São geradas por equipamentos electrónicos tais
como osciladores LC. Usadas para comunicação de rádio e televisão.
Luz visível. É a forma mais familiar dessas ondas. É aquela parte do espectro que o
olho humano pode detectar. A luz é produzida por corpos quentes. A sensibilidade dos
olhos é uma função do comprimento de onda. Para luz visível varia de 4 10 7 m
(violeta) até 7 10 7 (vermelho).
Raios gama. São OE emitidas por núcleos radioactivos e durante determinadas reacções
nucleares. > 10 10 m . São altamente penetrantes e produzem sérios danos em tecidos
vivos. Usam-se camadas de chumbo para protecção.
9