Problemas - DEC/FCT/UNL

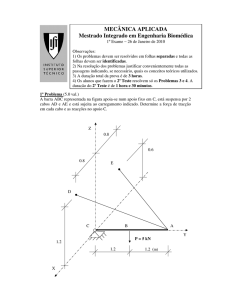
Problema 1
Considere que a estrutura representada na figura E
B
C
se encontra, num certo instante de tempo, na
30º
posição mostrada. Sabendo ainda que nesse
60 º
vB

aC
instante a velocidade no ponto B é de 3m/s
(com a direcção e sentido definidos na figura) e
a aceleração angular da barra CD é nula,
D
A
determine:
a) a distância d
3m
4 ,5 m
d
b) as acelerações angulares de todas as barras.
c) a aceleração do ponto F posicionado no meio
da barra BC
Solução: a) d  2,31m ;  AB  0,369rad/s2 (horário),  BC  0,189rad/s2 (anti-horário),
4m
aF   0, 25; 2,11 m/s2
Problema 2
A barra AB encontra-se em movimento. Num
instante particular encontre-se na posição
mostrada na figura ao lado. Determine (nesse
mesmo instante) a velocidade angular e a
aceleração angular da barra, indicando os
respectivos sentidos. Justifique os cálculos.
Considere L=45cm, β=25º, γ=55º, δ=40º,
aA=20m/s2 e aB=15m/s2.
Solução:   9, 48rad/s ;   40,86rad/s2 (horário)
Problema 3
No instante t a estrutura da figura encontra-se na
posição mostrada e tem a velocidade angular e a
aceleração angular da barra CD tal como designado
na figura. Calcule neste instante as velocidades
angulares e as acelerações angulares de todas as
barras. Determine ainda o vector da velocidade e da
aceleração do ponto C.
Nota: Determine o grau de liberdade cinemática.
Diga porque este valor é importante saber.
Determine e marque claramente a posição dos CIRs.
Use os CIRs para o cálculo das velocidades.
Apresente os esboços utilizados para o cálculo.

aA

L
A

aB


B
C
B
  3rad / s2
3
  5rad / s
4
A
2
2
D
3
Solução: AB  15 / 4rad/s2 (horário); BC  35 / 6rad/s2 (anti-horário); vC  15;10 m/s
 AB  42,8rad/s2 (horário);  BC  20, 28rad/s2 (anti-horário); aC   41; 81 m/s2
m
R
C
B
D
F
L
Problema 4
Considere o mecanismo representado na
figura, formado por duas barras (barra 1 AB e barra 2 -BC) articuladas de
comprimento L=0.5m e por um disco de
raio R=0.1m, que roda livremente e sem
escorregar. Assumindo que na posição
apresentada na figura, a velocidade e
aceleração angular da barra 1 são
1=4rad/s e 1=1rad/s2 em sentido antihorário, respectivamente, determine, para
o instante representado:
a)
As velocidades angulares da barra
2, 2 , e do disco, 3 ;
b)
As acelerações angulares da barra
2,  2 , e do disco,  3 ;

A
L
Solução: 2  0 , 3  20rad/s (anti-horário), 2  16rad/s2 (anti-horário), 3  5rad/s2
(anti-horário),
C
B
Problema 5
Sabendo a aceleração do ponto C, calcule as
acelerações de todas as barras na posição 4
mostrada.
Solução para ac=16m/s2:
sentido de velocidades angulares indeterminável:
AB  CD  1,861rad/s , BC  1,241rad/s (oposto)
aC
D
A
3
m
4,5
CD  2rad/s2 (horário),  AB  6,33rad/s2 (horário), BC  4,22rad/s2 (anti-horário),
Solução para ac=4m/s2: AB  CD  0,931rad/s , BC  0,620rad/s , CD  0,5rad/s2
(horário),  AB  1,583rad/s2 (horário), BC  1,055rad/s2 (anti-horário).
Problema 6
Na posição mostrada, a barra AB tem uma
velocidade angular de 1 rad/s no sentido antihorário e uma aceleração angular de 1 rad/s2
no sentido horário. Determine as velocidades
e as acelerações angulares das barras BD e
DE.
Solução:
BD  0,090rad/s (anti-horário),
DE  0,946rad/s (horário),
 BD  2,357rad/s2 (horário),  DE  0,629rad/s2
(anti-horário),
A
8
cm
D
12
8
E
B
10
15
12
60º
Problema 7
Na posição mostrada, a velocidade e a aceleração do
ponto B são como mostrado na figura. Determine as
velocidades e as acelerações angulares de todas as
barras.
Solução:
AC  0 , CD  0,25rad/s (horário),
A
8
2m/s 2
8m/s
D
B
16
E
C
4
 m
12
DE  0,2rad/s (anti-horário),
 AC  0 , CD  28,65 103 rad/s2 (anti-horário), DE  9,58 103 rad/s2 (horário)
15
Problema 8
O disco mostrado possui uma velocidade angular constante de 360rpm no sentido
horário. Determine a aceleração do cursor C quando (a) θ=0º e (b) θ=180º.
Solução: a) aC  79,94m/s2  , b) aC  133,24m/s2 
Problema 9
O tambor com 150mm de raio rola sem escorregar numa correia que se desloca para a
esquerda com a velocidade constante de 300mm/s. No instante em que a velocidade e a
aceleração do centro D do tambor têm os valores indicados, determine as acelerações dos
pontos A, B e C do tambor e do C da correia.
Solução: aA  1,80; 7,35 m/s2 , aB   6, 45; 0,90 m/s2 , aC ,T   0;7,35 m/s2 , aC ,C   0;0
Problema 10
Sabendo que a barra AB gira com velocidade


angular  e aceleração angular  , ambas no
sentido anti-horário, deduza as expressões para a
velocidade e a aceleração do cursor C.
Solução: aC  2L  sin    2 cos   
Problema 11
Sabendo que o cursor C se move para direita com
velocidade constante v0, deduza as expressões para
a velocidade angular e a aceleração angular da
barra AB.
v0
v2 cos
Solução:  
(horário),   02 3 (horário)
2 L sin 
4L sin 
Problema 12
Na posição indicada, a barra AB tem uma velocidade
angular constante de 0.2 rad/s no sentido horário.
Determine e represente graficamente:
a) A velocidade angular das barras BC e CD;
b) A velocidade dos pontos B e C;
c) A aceleração angular das barras BC e CD;
d) A aceleração dos pontos B e C.
Solução: a) BC  0, 2rad/s (anti-horário), CD  0,0167rad/s (anti-horário)
b)
vB  0,028m/s  ,
vC  0,02m/s  ;
c)
 BC  0,0026rad/s2
(horário),
CD  0,0936rad/s2 (horário); d) aB   0,0056;0 m/s2 , aC   0, 0112;3,33 105  m/s 2
Problema 13
Resolva as velocidades e as acelerações
angulares de todas as barras.
Solução: AC  0 , EC  1/ 2rad/s (horário),
CD  1/ 3rad/s (anti-horário),  AC  0 ,
EC  1/ 4rad/s2 (anti-horário),
CD  1/12rad/s2 (anti-horário)
Problema 14
Para a figura ao lado determine a norma da
velocidade do ponto B e a norma da aceleração
do centro de massa da barra AB, sabendo que
a barra AC tem velocidade angular 3rad/s no
sentido anti-horário e aceleração angular
4rad/s2, no sentido horário.
Solução: vB  12m/s , aG  39, 4m/s2
A
B
7m
C
4m
Problema 15
Considere o seguinte corpo rígido animado de
um movimento plano para o qual se conhece a
aceleração em dois pontos num determinado
instante:
aA  25m/s2  , aB  100m/s2 
Determine a aceleração e a velocidade
angulares.
Solução:   12,5rad/s2 (anti-horário),   5rad/s
Problema 16
Considere o seguinte corpo rígido animado de
um movimento plano para o qual se conhece a
velocidade vA   4,3 m/s e a aceleração
aA   2,0 m/s no ponto A. Sabe-se ainda
que nesse mesmo instante a velocidade e a
aceleração angulares são 3rad/s e 1,5rad/s2,
nos sentidos anti-horário e horário,
respectivamente.
a) Determine a aceleração e a velocidade no ponto B.
b) Determine a componente normal de aceleração no ponto A.
Solução: vB   7; 9 m/s , an, A  1, 2m/s2