Vetores Forças Cap. 2

Objetivos
Mostrar como somar forças e decompô-las em
componentes usando a lei do paralelogramo.
Expressar a força e a sua localização na forma
vetorial cartesiana e explicar como determinar a
intensidade e a direção dos vetores.
Introduzir o conceito de produto escalar para
determinar o ângulo entre dois vetores ou a projeção
de um vetor sobre o outro.
MECÂNICA - ESTÁTICA
Vetores Forças
Cap. 2
Prof Dr. Cláudio Curotto
Adaptado por:
Prof Dr. Ronaldo Medeiros-Junior
TC021 - Mecânica Geral I - Estática
2.1 Escalares e Vetores
2
2.2 Operações com Vetores
Escalar é uma grandeza caracterizada por um número
positivo ou negativo; exemplos: massa, volume e
comprimento.
Vetor é uma grandeza que possui módulo, direção e
sentido; exemplos: posição, força e momento.
Multiplicação e Divisão de um Vetor por um Escalar:
Multiplicação do vetor A pelo escalar a ⇒ aA
Mesmo sentido de A se a > 0; contrário se a < 0
Divisão do vetor A pelo escalar a ⇒ (1/a)A ; a ≠ 0
ϴ = Direção
TC021 - Mecânica Geral I - Estática
3
2.2 Operações com Vetores
TC021 - Mecânica Geral I - Estática
4
2.2 Operações com Vetores
Adição Vetorial:
Dois vetores adicionados formam o vetor resultante R
⇒ A + B = B + A = R
(comutativo)
Adição Vetorial:
Lei do paralelogramo
A partir da extremidade de B, desenhe uma linha paralela a A. Desenhe outra
linha a partir da extremidade de A que seja paralela a B. Essas duas linhas
se interceptam no ponto P para formar os lados adjacentes de um
paralelogramo.
A diagonal desse paralelogramo que se estende até P forma R, que então
representa o vetor resultante R = A + B
Lei do paralelogramo
Regra do triângulo
TC021 - Mecânica Geral I - Estática
5
TC021 - Mecânica Geral I - Estática
6
1
2.2 Operações com Vetores
2.2 Operações com Vetores
Adição Vetorial:
Adição Vetorial:
Vetores colineares
Regra do triângulo (extremidade-para-origem)
Conectar a extremidade de A à origem de B. O R resultante se estende da
origem de A à extremidade de B.
TC021 - Mecânica Geral I - Estática
7
TC021 - Mecânica Geral I - Estática
8
2.3 Adição de Forças Vetoriais
2.2 Operações com Vetores
Subtração Vetorial (*caso especial da adição):
A diferença entre dois vetores produz o vetor
resultante R’
⇒ A - B = A + (-B) = R´
Uma força é uma grandeza vetorial pois tem
módulo, direção e sentido e pode ser adicionada
de acordo com a regra do paralelogramo.
Duas forças agindo
sobre o gancho
TC021 - Mecânica Geral I - Estática
9
2.3 Adição de Forças Vetoriais
F2
F1
F2
TC021 - Mecânica Geral I - Estática
10
Procedimento de Análise
As duas forças componentes, F1 e F2, agindo sobre o pino podem
ser somadas para formar a força resultante FR = F1 + F2. A partir
dessa construção, ou usando a regra do triângulo, pode-se aplicar
a lei dos cossenos ou a lei dos senos para o triângulo a fim de
obter a intensidade da força resultante e sua direção.
F1
TC021 - Mecânica Geral I - Estática
Para encontrar o módulo da resultante C use a Leis
dos cosenos
F2
F1
FR
A+B=C
FR
11
TC021 - Mecânica Geral I - Estática
12
2
2.3 Adição de Forças Vetoriais
2.3 Adição de Forças Vetoriais
Decomposição Vetorial:
Se mais do que duas forças precisam ser adicionadas,
Se uma força F precisa ser decomposta em componentes ao longo de dois
eixos u e v, então, iniciando na extremidade da força F, deve-se contruir
linhas paralelas aos eixos, formando, assim, o paralelogramo. Os lados do
paralelogramo representam as componentes, Fu e Fv.
⇒R=A+B
u
sucessivas aplicações da regra do paralelogramo
devem ser utilizadas para obter a resultante.
⇒ F1 + F2 + F3 = (F1 + F2) + F3
u
F
F
Fu
v
v
Fv
TC021 - Mecânica Geral I - Estática
13
Pontos importantes
TC021 - Mecânica Geral I - Estática
14
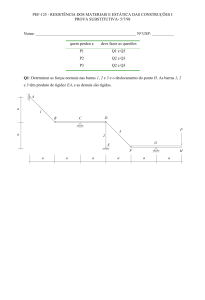
Problema 2.2
Determine o módulo da força resultante se:
(a) FR = F1 + F2
(b) FR′ = F1 – F2
TC021 - Mecânica Geral I - Estática
15
Problema 2.2
TC021 - Mecânica Geral I - Estática
16
Problema 2.2
(a) Adição Vetorial: Usando a regra do paralelogramo:
FR = 100 2 + 80 2 − 2(100 )(80) cos 75° = 111N
(b) Subtração Vetorial:
90 - 45= 450
60 + 45= 1050
R
(2*105) + (2*ϴ)= 3600
100N
?=1050
80N
?=750
?=450
600
450
TC021 - Mecânica Geral I - Estática
R
750
80N
17
TC021 - Mecânica Geral I - Estática
18
3
Problema 2.A
Exemplo 2.2
Dadas as duas forças mostradas pela figura.
a. Calcule a resultante das duas forças.
b. Decomponha as duas forças nas direções u e v
Decomponha a força de 200-lb atuando no tubo
em componentes
v
(a) direções x e y, e
u
180N
(b) direções x’ e y.
150N
20°
40°
15
°
TC021 - Mecânica Geral I - Estática
19
Exemplo 2.2
TC021 - Mecânica Geral I - Estática
20
Exemplo 2.2
Usando a regra do paralelogramo para decompor F
Parte (a)
A adição vetorial é dada por F = Fx + Fy
Do triângulo abaixo:
⇒Fx = 200 lb cos 40° = 153 lb
e Fy = 200 lb sin 40 ° = 129 lb
⇒
TC021 - Mecânica Geral I - Estática
⇒
21
Exemplo 2.2
TC021 - Mecânica Geral I - Estática
Exemplo 2.2
Parte (b):
Aplicando a regra do paralelogramo:
A adição vetorial é dada por F = Fx′ + Fy
⇒
TC021 - Mecânica Geral I - Estática
22
⇒
23
TC021 - Mecânica Geral I - Estática
24
4
Exemplo 2.2
Aplicando a lei dos senos:
Fx '
200lb
=
sin 50° sin 60°
 sin 50° 
⇒ Fx ' = 200lb 
 = 177lb
 sin 60° 
Fy
200lb
=
sin 70° sin 60°
 sin 70° 
⇒ Fy = 200lb 
 = 217lb
 sin 60° 
TC021 - Mecânica Geral I - Estática
25
5