9. Estrutura dos atomos II Ficheiro - Moodle

Níveis de energia do átomo
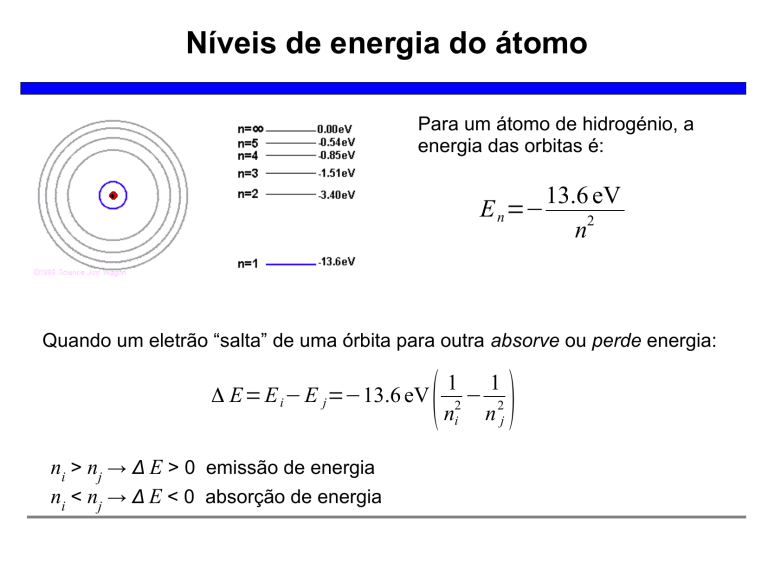
Para um átomo de hidrogénio, a
energia das orbitas é:
13.6 eV
E n =−
n2
Quando um eletrão “salta” de uma órbita para outra absorve ou perde energia:
1 1
Δ E= E i − E j =−13.6 eV 2 − 2
ni n j
(
ni > nj → Δ E > 0 emissão de energia
ni < nj → Δ E < 0 absorção de energia
)
A física quântica
A física quântica revoluciona a nossa percepção da natureza.
As ideias de base são:
1. As partículas materiais são descritas por ondas.
2. Quando se efectua a observação/medição de uma grandeza física o estado
da onda que descreve as partículas altera-se
3. O resultado da medição está intrinsecamente afectado de uma incerteza
4. Ao valor de cada grandeza física está portanto associada uma
probabilidade de se obter um esse resultado. Essa probabilidade é dada pelo
quadrado da amplitude da função de onda alterada.
Ondas estacionarias
Na realidade, os electrões são objectos tridimensionais. Então como é que
são as ondas estacionarias em duas e três dimensões ?
Como vibra um tambor?
Podemos dar um
nome a cada
maneira de oscilar
usando dois
números:
(A,B):
A → Numero de
diâmetros nodais
B → Numero de
circunferências nodais
Orbitais atómicos
Os orbitais atómicos
têm uma forma
complicada porque são
ondas estacionarias em
três dimensões.
Estas ondas são
interpretadas no âmbito
da Física quântica
como ondas de
probabilidade!
Em três dimensões
cada maneira de
oscilar é indicada por
três números.
Os números quânticos
Cada orbital é univocamente individuado por três números. Quais são estes
números? São chamados números quânticos e têm o seguinte significado:
Número quântico principal:
n ← Raio do orbital e energia do orbital
Número quântico azimutal: l ← Momento angular:
especifica a forma do orbital
Número quântico magnético: m ← Componente do momento angular
ao longo dum eixo específico: individua a orientação do orbital
Estes números vêm da quantização da energia e do momento
angular. As quantidades físicas são individuadas por números
inteiros.
Um electrão é também caracterizado pelo spin
Número quântico de spin: s ← Momento magnético de spin
Os números quânticos
Quais são os valores possíveis para os números quânticos?
Número quântico principal: n = 1, 2, 3, 4, ... oo;
Número quântico azimutal: l = 0, ..., n-1; [Há n valores diferentes]
Número quântico magnético: m = -l, -l+1, ..., l-1, l; [Há 2l+1 valores diferentes]
Número quântico de spin: ms = -1/2 ou +1/2
Por razões históricas é usual usar-se letras para escrever os números quânticos
principal e azimutal:
n=1
n=2
n=3
n=4
n=5
usa-se K
usa-se L
use-se M
usa-se N
usa-se O
l=0
l=1
l=2
l=3
l=4
usa-se s (sharp);
usa-se p (principal);
usa-se d (diffuse);
usa-se f (fundamental);
usa-se g (....).
Nos usamos esta notação:
nly
número de
electrões
letra
Ex. 1s1, 1s2 2p3
Configurações electrónicas
Princípio da energia mínima:
sempre que possível os electrões ocupam as orbitais de menor energia;
Princípio de exclusão de Pauli:
não podem existir dois electrões num átomo com o mesmo conjunto de números
quânticos;
Regra de Hund:
as orbitais com a mesma energia devem ser primeiro semipreenchidas com
electrões com o mesmo spin e só depois se procede ao emparelhamento dos
spins (este maximiza o spin total).
Um átomo (electricamente neutro) tem um número de electrões (carga negativa)
igual ao número de protões do núcleo (carga positiva).
Exemplos
Nota
O número quântico principal n define o nível energético de base. Os outros
números quânticos especificam o tipo de orbitais mas a relação com a
energia pode ser complicada.
Exemplos:
Energy
K:
Ca:
Sc:
Ti:
V:
Cr:
Mn:
Fe:
1s2 2s2 2p6 3s2 3p6 4s1
1s2 2s2 2p6 3s2 3p6 4s2
1s2 2s2 2p6 3s2 3p6 3d1 4s2
1s2 2s2 2p6 3s2 3p6 3d2 4s2
1s2 2s2 2p6 3s2 3p6 3d3 4s2
1s2 2s2 2p6 3s2 3p6 3d5 4s1
1s2 2s2 2p6 3s2 3p6 3d5 4s2
1s2 2s2 2p6 3s2 3p6 3d6 4s2
...
3d
3s 3p
2s
1s
2p
4s
4p
Exercício
Quantos electrões podem acomodar os orbitais:
s:
p:
d:
f:
g:
Nota
Nas transições atómicas entre dois níveis de uma átomo dá-se a absorção ou
emissão de um fotão com energia igual à diferença de energias das órbitas
atómicas. No caso do átomo de hidrogénio, temos:
h ν=
hc
1 1
=−13.6 eV 2 − 2
λ
ni n j
(
)
ou seja (hc=1.986x10-25 Jm ≈ 1240 eV nm)
1 −13.6 eV 1 1
1 1
=
−
=−R
− 2
2
2
2
λ
hc
ni n j
ni n j
(
) (
)
onde R=13.6/1240 nm-1 = 1.097x10-2 nm-1 chama-se constante de Rydberg.