GEOMETRIA – AULA 07 – Soluções

GEOMETRIA – AULA 07 – Soluções
Prof. Antonio (Prof. Tuca)
POTI – Pirassununga.
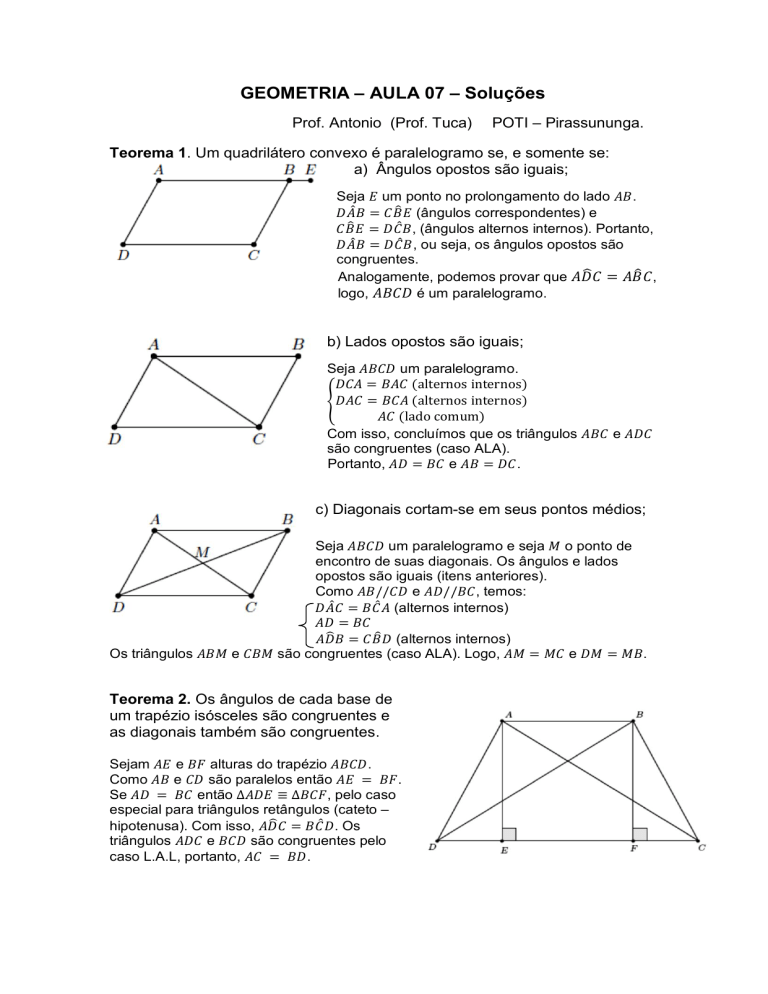
Teorema 1. Um quadrilátero convexo é paralelogramo se, e somente se:
a) Ângulos opostos são iguais;
Seja
um ponto no prolongamento do lado
.
(ângulos correspondentes) e
, (ângulos alternos internos). Portanto,
, ou seja, os ângulos opostos são
congruentes.
Analogamente, podemos provar que
,
logo,
é um paralelogramo.
b) Lados opostos são iguais;
Seja
um paralelogramo.
Com isso, concluímos que os triângulos
são congruentes (caso ALA).
Portanto,
e
.
e
c) Diagonais cortam-se em seus pontos médios;
Seja
um paralelogramo e seja o ponto de
encontro de suas diagonais. Os ângulos e lados
opostos são iguais (itens anteriores).
Como
e
, temos:
(alternos internos)
Os triângulos
e
(alternos internos)
são congruentes (caso ALA). Logo,
Teorema 2. Os ângulos de cada base de
um trapézio isósceles são congruentes e
as diagonais também são congruentes.
Sejam
e
alturas do trapézio
.
Como
e
são paralelos então
.
Se
então
, pelo caso
especial para triângulos retângulos (cateto –
hipotenusa). Com isso,
. Os
triângulos
e
são congruentes pelo
caso L.A.L, portanto,
.
e
.
Teorema 3. As diagonais do losango
são perpendiculares.
Como o losango é um paralelogramo,
então as diagonais cortam - se em seus
pontos médios, ou seja,
e
. Com isso, os triângulos
e
são congruentes, pelo caso LLL,
portanto,
.
Como
, temos:
Isso mostra que AC é perpendicular a BD, ou seja, as diagonais são perpendiculares.
Teorema 4. As diagonais de um retângulo são iguais.
Os triângulos
caso LAL.
e
são congruentes pelo
é lado comum.
Portanto,
Problema 1. Sejam
e
os segmentos iguais e paralelos.
Traçamos os segmentos
e
, que se intersectam em .
(alternos internos)
(alternos internos)
Pelo caso LAL, os triângulos
e
são congruentes.
Como
e
, então
é um paralelogramo.
https://www.youtube.com/watch?v=bahmzbij6_I&index=2&list=P
L8v7luSb9qi77-eVD5wmPZa6dcmLMovbx
Problema 2.
Seja
um ponto na base do triângulo isósceles
e sejam
e
os segmentos paralelos aos lados
e
,
respectivamente. AFDE é um paralelogramo, pois
e
. Portanto,
.
Os triângulos
e
são isósceles,
assim
.
Calculamos o perímetro do paralelogramo
:
A soma dos lados congruentes do triângulo
Como
e
é:
, temos que:
, então
, daí:
O perímetro é igual à soma dos comprimentos
dos lados congruentes.
https://www.youtube.com/watch?v=WQlenDGm5Dc&index=3&list=PL8v7luSb9qi77eVD5wmPZa6dcmLMovbx
Problema 3.
Como
Sendo
Como
, então
(alternos internos).
Sendo
bissetriz do ângulo , então
, logo o triângulo
é
isósceles e
.
Como
(enunciado) e
, então
.
O triângulo
é isósceles, assim:
.
temos que
(alternos internos).
, concluímos que
é bissetriz do ângulo .
https://www.youtube.com/watch?v=sshDdfqOouE&index=4&list=PL8v7luS
b9qi77-eVD5wmPZa6dcmLMovbx
Problema 4.
e
são
paralelogramos de
diagonais
,
e
e
,
respectivamente.
Como as diagonais de um
paralelogramo cortam-se em
em seus pontos médios e
é uma diagonal comum, o
ponto médio de
é o ponto
médio de
e de
.
Logo,
é um quadrilátero cujas diagonais
e
cortam-se em seus pontos médios.
Sendo
um paralelogramo então
.
Problema 5.
Seja o ponto no prolongamento de
, tal que
.
Como AB=AD e ABL=90°=ADM, então
Os triângulos
e
são congruentes
pelo caso LAL. Assim:
e
.
No triângulo KAL, temos que:
, como
,
vem:
, mas
é
bissetriz do ângulo
, então
, daí:
⇒
Como
, temos que
, logo
.
O triângulo é isósceles, então:
e
, daí:
, como
, temos que:
, ou seja