Física Geral I - F -128
Aula 14
Conservação do Momento
Angular; Rolamento
Cinemática de Rotação
z
Variáveis Rotacionais
Deslocamento angular:
Δθ (t ) = θ (t +Δt ) −θ (t )
Velocidade angular média ω =
Δθ
Δt
y
θ
x
Velocidade angular instantânea
Δθ dθ
ω = lim
nˆ = nˆ
Δt →0 Δt
dt
!
!
Δω
Aceleração angular média α =
Δt
!
!
Aceleração angular instantânea α! = lim Δω = dω
Δt → 0 Δt
dt
F128 – 2o Semestre de 2012 "
2 Cinemática de Rotação
Relação com as variáveis lineares
• Posição: s= r θ
• Velocidade:
!
α
!
a
!
t
!a N
r
! ! !
v =ω × r
$
$ dω $ $ dr
• Aceleração: a =
×r +ω ×
dt"! #"!
dt
#
!
!
aN
at
! ! !
at = α ×r = α r vˆ
! ! ! ! ! !
a N = ω ×v = ω ×(ω ×r ) = − ω 2 r rˆ
!
v
θ
$
F128 – 2o Semestre de 2012 ẑ
!
ω
ŷ
s
x̂
z
y
θ
x
3 Rotação em torno de um eixo fixo
Tabela de analogias
Rotação em torno
de um eixo fixo
energia cinética
equilíbrio
2a lei de Newton
2a lei de Newton
momento
conservação
potência
F128 – 2o Semestre de 2012 1
KR= Iω2
2 !
!
∑τ = 0
! !
τ
∑ =Iα !
Movimento de
translação
1
K = mv 2
!2 !
∑F =0
!
!
∑F =ma
dL
τ
=
∑ ( ext ) dt
! dp!
∑F = dt
! !
Li =L f
P =τ ω
P= F v
!
L = Iω
!
!
p =mv
! !
p i= p f
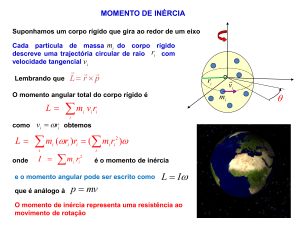
4 Momento Angular
"
!
O momento angular ℓ de uma partícula de momento p
em relação ao ponto O é:
! ! !
ℓ=r× p
(Note que a partícula não precisa estar girando em torno
de O para ter momento angular em relação a este ponto).
d d
= (r × p) = r × F = τ
dt
dt
dL
Para um sistema de partículas, τ ext =
dt
Para um corpo rígido em torno de um eixo fixo, L = Iω
Se τ / τ ext = 0 , então o momento angular é constante no tempo!
F128 – 2o Semestre de 2012 5 Conservação do momento angular
No sistema homem – halteres: só há forças internas e, portanto:
L( z ) =Iω = constante ⇒ I iωi =I f ω f
ωi I i
ωf I f
Com a aproximação dos halteres ( I f < I i ) a velocidade angular
do sistema aumenta.
F128 – 2o Semestre de 2012 6 Conservação do momento angular
O mesmo princípio se aplica na patinação artística:
L( z ) =Iω = constante ⇒ I iωi =I f ω f
http://www.youtube.com/watch?v=AQLtcEAG9v0
F128 – 2o Semestre de 2012 7 Exemplo
Dados
I bic = 1, 2 kg.m 2 ; I tot = 6,8 kg.m 2 e ωi = 3,9 rot/s
Queremos calcular a velocidade angular
final ω do sistema após o menino inverter o
eixo de rotação da roda de bicicleta (ver
figura)
Momento angular inicial do sistema
roda de bicicleta-menino (+ banco)
Li = Lbic = I bicωi
O menino inverte o eixo de rotação
da roda de bicicleta
Lbic → − Li
F128 – 2o Semestre de 2012 8 Exemplo
Momento angular final do sistema:
L f = Lbic + Lmen = Lmen − Li
Conservação do momento angular
(pois só há forças internas no sistema)
L f = Li ⇒ Lmen − Li = Li
⇒ Lmen = 2 Li
I tot ω =2I bicωi
2 I bic ωi
ω=
≅ 1,4 rot/s
I tot
F128 – 2o Semestre de 2012 9 Conservação do momento angular
No caso da mergulhadora da figura ao lado o CM segue um
movimento parabólico.
Nenhum torque externo atua sobre ela em relação a um eixo que
passa pelo CM; então no referencial do CM:
!
dL′
! !
! !
= ∑ ri ′ × Fi = ∑ mi ri ′ × g = 0
dt
i
i
$
#"
=0
!
e o momento angular L ′ da nadadora é constante
durante o salto. Juntando braços e pernas, ela
pode aumentar sua velocidade angular em torno
do eixo que passa pelo CM, às custas da redução
do momento de inércia em relação a este eixo.
F128 – 2o Semestre de 2012 !
LL′′
⊗
!
Mg
Mg
10 Movimento de um corpo rígido
O tipo mais geral de movimento de um CR é uma combinação de
uma translação com uma rotação.
F128 – 2o Semestre de 2012 11 Rolamento (sem deslizamento)
Ø O
deslocamento do centro de massa e a rotação estão vinculados:
Ø s é o deslocamento do centro de massa do objeto
Ø θ é o deslocamento angular do objeto em torno de um eixo que
passa pelo CM do sistema.
vCM
R
θ
s
s= Rθ
A velocidade do CM é dada por:
F128 – 2o Semestre de 2012 ds dθ
vCM = = R = Rω
dt
dt
12 Rolamento (sem deslizamento)
Decomposição do rolamento em rotação + translação
Rotação
pura
Translação
pura
!
vCM
!
vCM
!
vCM
v = vCM = Rω
F128 – 2o Semestre de 2012 Translação
+ Rotação
!
2 vCM
v =ω R
+
v =0
=
v=−ω R
v = rω (acima do centro)
v = −rω (abaixo do centro)
!
vCM
v =0
O ponto de contato está
sempre em repouso.
13 Rolamento (sem deslizamento)
Fotografia de uma roda em rolamento
!
2 vCM
!
vCM
v =0
Figura da esquerda: o rolamento sem deslizamento pode ser descrito como uma
rotação pura com a mesma velocidade angular ω em torno de um eixo que sempre
passa pelo ponto P de contacto (eixo instantâneo de rotação).
De fato:
v P′ =ω 2R= 2 ω R = 2vCM
Figura da direita: os raios de cima estão menos nítidos que os de baixo porque
estão se movendo mais depressa.
F128 – 2o Semestre de 2012 14 Energia cinética de rolamento
Encarando o rolamento sem deslizamento como uma rotação pura
em torno do eixo instantâneo:
1
K= IPω 2
2
Mas I P = I CM + M R 2 (teorema dos eixos paralelos)
!
2v
Então:
1
1
2
K = I CM ω + M R 2 ω 2
!
2
2
vCM
1
1
2
2
K = I CM ω + M vCM
2
2
Isto é, a energia cinética do corpo rígido é a
v =0
soma da energia cinética de rotação em torno do
CM com a energia cinética associada ao movimento
de translação do CM.
CM
F128 – 2o Semestre de 2012 15 Exemplo
O iô-iô
Torque externo relativo ao CM quando
o iô-iô desce:
r
T
Tr= I CM α
Dinâmica linear (eixo orientado para baixo)
Mg
Mg −T = Ma
Condição de rolamento:
Mg
T=
Mr 2
1+
I CM
F128 – 2o Semestre de 2012 v =ω r ⇒ a =α r
e
r2
a=
T=
I CM
g
I CM
1+
Mr 2
16 Exemplo
Note que se o iô-iô sobe, o torque muda
de sinal
− Tr= I CM α
r
T
Por outro lado, o fio se enrola e a
condição de rolamento também muda
de sinal
v = −ω r ⇒ a = − α r
Mg
Ao final, as equações não mudam!
T r = − I CM α = I CM
Ma = Mg −T
F128 – 2o Semestre de 2012 a
r
Mg
T=
Mr 2
1+
I CM
r2
e a=
T=
I CM
g
I CM
1+
Mr 2
17 Exemplo
Podemos ainda resolver o mesmo problema
usando a conservação de energia:
1 2 1
MvCM + I CM ω 2 = M g z
2
2
r
Z
T
A condição de rolamento é
Mg
2gz
vCM = ±
= ± 2a z
vCM =ω r
I CM
1+
Mr2
Sinal (+) para a descida e (–) para a subida.
Equação de Torricelli com aceleração constante dada por
g
a=
I CM
1+
M ρ2
F128 – 2o Semestre de 2012 18 Rolamento (sem deslizamento)
Atrito no rolamento
!
ω
!
Fa
ω
!
⊗ ττ
!
Mg
Corpo rolando ladeira
abaixo devido ao próprio
peso.
F128 – 2o Semestre de 2012 Transforma
energia cinética
de translação em
rotação
Transforma
energia cinética
de rotação em
translação
ω
!
!
ω ⊗ ττ
!
M
g
Mg
!
FFaa
Roda de um carro girando.
19 Exemplo
Rolamento sobre um plano inclinado
Na direção y:
N − Mg cosθ = 0
Na direção x:
Mgsen θ −Fa = Ma
!
vCM
Torque relativo ao CM:
Fa R = I CM α
y
Condição de rolamento sem
deslizamento: a = Rα
Momento de inércia: I CM = Mk
( k é o raio de giração)
F128 – 2o Semestre de 2012 !
N
!
vCM
x
2
!
Fa
Mgcos θ
!
Mgsen
vCM θ
!
Mg
20 Exemplo
Rolamento sobre um plano inclinado
g sinθ
a=
I CM
1+
MR 2
⎧2
I
⎪
Se 1+ CM2 = ⎨3/ 2
R
⎪7 / 5
⎩
Temos ainda:
Fa = Mgsenθ
!
N
y
!
vCM
x
anel
cilindro
!
Fa
Mgcos θ
esfera
Mgsen θ
!
Mg
I CM
≤ µ e N = µ e Mg cosθ ∴
2
I CM + MR
I CM + MR 2
tgθ ≤ µ e
≡ tgθ r
I CM
F128 – 2o Semestre de 2012 Ângulo máximo (limiar) para que
haja rolamento sem deslizamento
21 Precessão do momento angular
Se a roda tem uma velocidade angular
ω grande, seu eixo gira em torno do eixo z,
como veremos ( movimento de precessão).
O torque da força peso é:
! !
! !
ao eixo
τ = r × Mg ( τ é perpendicular
!
e ∴ ao momento angular L da roda.
!
!
! dL
Como τ =
, segue que dL é
!
dt
perpendicular a L
!
Então o módulo de L não varia, e o
que muda é apenas a sua direção.
F128 – 2o Semestre de 2012 22 Precessão do momento angular
Roda
Temos: dL =τdt =Mgrdt e da figura:
dL = Ldϕ = Iω dϕ ∴
dL Mgrdt
dϕ = =
L
Iω
Velocidade angular de precessão:
dϕ Mgr
Ω=
=
dt
Iω
Note que este resultado também é válido
quando o eixo do giroscópio (roda) faz um
ângulo diferente de zero com a horizontal (ver
exemplo do pião, a seguir)
F128 – 2o Semestre de 2012 !
Li
!
dL
!
Lf
23 Giroscópio
http://www.youtube.com/watch?v=8H98BgRzpOM
F128 – 2o Semestre de 2012 24 Precessão do momento angular
Pião
Módulo do torque da força peso:
!
L
θ
τ =Mgr senθ
!
N
Lei fundamental da dinâmica das rotações:
! !
ΔL = τ Δt
!
Mg
ΔL=Mg r senθ Δt
!
τ
Da figura temos:
ΔL= L senθ Δϕ = Iω senθ Δϕ ∴
Mgr senθ Δt =Iω senθ Δϕ
Velocidade angular de precessão:
dϕ Mgr
Ω≡
=
dt
Iω
F128 – 2o Semestre de 2012 Δϕ
25 Precessão do momento angular
O centro de massa do pião executa
movimento circular com uma aceleração
centrípeta
!
L
θ
a c = Ω 2 r senθ
!
N
A força de atrito pião-piso é a
responsável por esta aceleração
!
Mg
!
Fa
!
τ
Fa =MΩ 2 r senθ
Fa ≤ µ Mg
Como
senθ ≤
µg
Ω2r
F128 – 2o Semestre de 2012 para que a ponta do pião
fique fixa e haja apenas
movimento de rotação!
Δϕ
26 Um giroscópio
!
L
!
N
F128 – 2o Semestre de 2012 !
Mg
27 Precessão do momento angular
Como a Terra é um esferóide oblato (achatado nos polos), a Lua e
o Sol provocam forças como as mostradas abaixo e em 13.000 anos o
eixo de rotação sofre precessão de meio período, como na figura.
F128 – 2o Semestre de 2012 28 FIM! L
F128 – 2o Semestre de 2012 29