Calor, Trabalho e a Primeira Lei da Termodinâmica

Calor, Trabalho e a Primeira Lei da Termodinâmica
Bibliografia e figuras: Halliday, Resnick e Walker, vol 2, 8a. Edição
• Vamos estudar como a energia pode ser transferida em forma de
calor e trabalho de um sistema físico para o ambiente e vice-versa.
• Considere, para isto, o seguinte sistema físico, isolado do exterior.
No equilíbrio: A força para cima que atua no êmbolo
devido à pressão do gás confiado é igual ao peso da massa de chumbo colocada sobre o êmbolo.
• Um sistema físico (gás) é levado de seu estado inicial, descrito
pelas variáveis de estado (pi,Vi, Ti) até um estado final, descrito
pelas variáveis de estado (pf, Vf, Tf) através de um processo
termodinâmico.
• Durante este processo, o gás pode receber energia (Q > 0) do
reservatório térmico ou ceder energia ( Q < 0) para o reservatório
térmico.
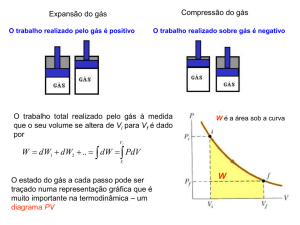
• Além disso, trabalho pode ser realizado pelo gás
(W > 0) sobre a
massa de chumbo, erguendo o êmbolo, ou trabalho pode ser
realizado sobre o gás (W < 0) onde a massa de chumbo comprime
o gás.
• Considere que tudo isto, ocorre bastante lentamente, de tal
maneira que o sistema encontra-se em equilíbrio térmico.
Vamos reduzir a massa de chumbo, de tal modo
que o gás empurre o êmbolo para cima com uma
força F (aproximadamente constante) produzindo
um deslocamento infinitesimal ds.
F =p·A
p é a presão que o gás exerce sobre a área A do êmbolo.
O trabalho infinitesimal realizado pelo gás é então:
~ = (pA)ds = p(Ads) = pdV
dW = F~ · ds
Neste processo, o volume varia de um volume inicial Vi até um volume final Vf,
portanto o trabalho total realizado pelo gás é:
W =
Z
Vf
dW =
Vi
Z
Vf
pdV
Vi
Observações importantes.
• Durante a variação do volume, a pressão e a temperatura do gás
também podem variar.
• Para calcularmos a integral que fornece o trabalho para levar ogás
de seu estado inicial para seu estado final, devemos saber como a
pressão varia com o volume. • Na prática existem muitas maneiras de levar o gás de seu estado
inicial até seu estado final e o cálculo do trabalho depende de
como se faz esta transição.
• Podemos representar a variação do estado de um gás em um
diagrama Pressão x Volume, ou diagrama pV.
• O cálculo do trabalho pode ser efetuado a partir destes diagramas.
Diagramas pV e Trabalho
Wicdf < Wighf
Conclusões importantes
•
Tanto o trabalho W quanto
o calor dependem do
caminho utilizado para levar
o sistema de seu estado
inicial para o estado final.
•
São grandezas físicas que
dependem do caminho
escolhido.
•
O trabalho pode ser
calculado pela área sob a
curva representando o
processo físico no diagrama
pV.
W = área sob a curva
A primeira lei da Termodinâmica
• Aprendemos que tanto W quanto Q variam em um processo
termodinâmico que leva um gás de seu estado inicial até seu estado
final.
• Entretanto, a grandeza Q-W não varia, seja qual for o caminho do
processo, dependendo somente dos estados inicial e final.
• Isto sugere que Q-W representa a variação de alguma
propriedade intrínseca (fundamental) do sistema.
• Vamos chamá-la de Variação da Energia Interna, ∆E
int,
sistema.
Eint =
f
Eint
i
Eint
=Q
W
do
Considerações importantes
• O trabalho W, é realizado pelo sistema
• Se o trabalho W, é realizado sobre o sistema, tem-se que
Wsobre= -W
• Neste caso, a primeira lei da termodinâmica pode ser escrita
como: ∆Eint = Q + Wsobre
• Consideremos agora alguns casos específicos da primeira lei da
Termodinâmica
• Processos adiabáticos:
• São aqueles que ocorrem tão depressa ou em um sistema tão
bem isolado que não há troca de calor entre o sistema e o
ambiente.
• Q = 0 e ∆E
int
= -W
• Processos a volume constante
• Se o volume do sistema é mantido constante, este não realiza
trabalho! • W = 0, ∆E
int
=Q
• Processos cíclicos:
• Neste caso nenhuma propriedade intrínseca do sistema varia,
incluindo a energia interna.
• ∆E
int
= 0, Q = W
• Expansões livres
• São processos adiabáticos (Q = 0 ) nos quais nenhum trabalho é
realizado (W = 0 ).
• Q = W = 0, ∆E
int
= 0.
Cálculo do trabalho em casos específicos
a) Quando a pressão é constante podemos escrever:
W =
Z
Vf
pdV = p
Vi
Z
Vf
dV = p(Vf
Vi ) = p V
Vi
b) Quando o volume é constante: dV = 0 e portanto W = 0 !
Quando temos um gás ideal onde vale pV=nRT e o processo ocorre com
temperatura constante faz-se p=nRT/V e portanto,
W =
Z
Vf
pdV = nRT
Vi
W = nRT ln
✓
Vf
Vi
◆
Z
Vf
Vi
dV
= nRT (lnVf
V
lnVi )