Escoamento Viscoso Externo - PUC-Rio

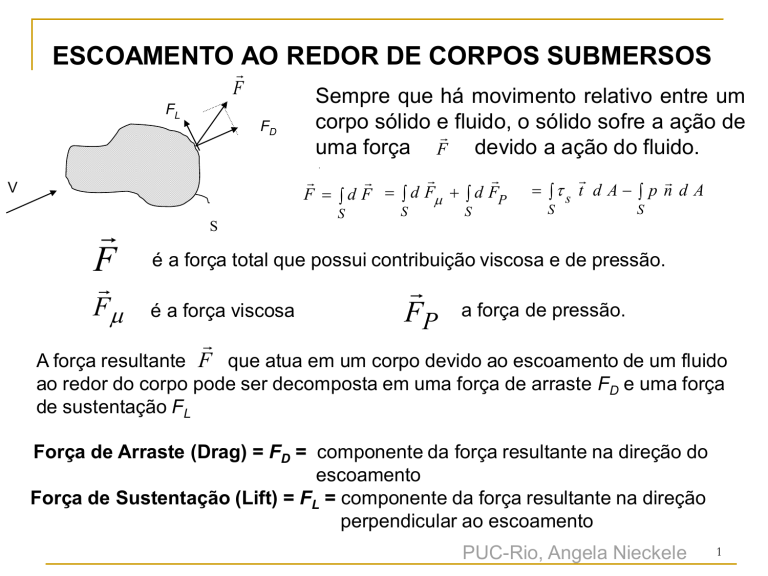
ESCOAMENTO AO REDOR DE CORPOS SUBMERSOS
F
FL
FD
Sempre que há movimento relativo entre um
corpo sólido e fluido, o sólido sofre a ação de

uma força F devido a ação do fluido.




F   d F   d F   d FP
V

F

F
S
S
S
S


 s t d A   p n d A
S
S
é a força total que possui contribuição viscosa e de pressão.
é a força viscosa

FP
a força de pressão.

A força resultante F que atua em um corpo devido ao escoamento de um fluido
ao redor do corpo pode ser decomposta em uma força de arraste FD e uma força
de sustentação FL
Força de Arraste (Drag) = FD = componente da força resultante na direção do
escoamento
Força de Sustentação (Lift) = FL = componente da força resultante na direção
perpendicular ao escoamento
PUC-Rio, Angela Nieckele
1
É conveniente adimensionar essas forças, para generalizar as análises e
os resultados. Define-se então:
Coeficiente de Arraste = CD
CD 
FD
1
 V 2 Aref
2
CD = CD ( geometria, Re)
Coeficiente de Sustentação = CL
CL 
FL
1
 V 2 Aref
2
Aref em geral é a área projetada na direção perpendicular ao escoamento
PUC-Rio, Angela Nieckele
2
CAMADA LIMITE
Fora da camada limite, o
escoamento não é afetado
pela presença do corpo 
forças viscosas não são
importantes
Região afetada pela
presença do corpo

CAMADA LIMITE
Quando o escoamento na camada limite é
desacelerado devido a uma diferença de
pressão, pode ocorrer uma reversão do
escoamento e a camada limite separa-se da
superfície do corpo, formando a esteira
3
Camada limite sobre uma placa plana
Espessura da camada limite: d(x)
A espessura da camada limite é
pequena, tornando o gradiente de
velocidade u/y muito alto  As
forças viscosas dentro da camada
limite são importantes
A equação de Navier-Stokes pode ser
simplificada baseada numa análise
dimensional e no fato que d é
pequeno, gerando uma equação mais
simples que descreve o escoamento
na camada limite.
A espessura da camada limite pode
ser calculada a partir da solução desta
equação.
PUC-Rio, Angela Nieckele
4
número de Reynolds local:
 0
Uo
d
y
x
laminar
turbulento
xc
L

 Uo x
Re x 

Reynolds crítico:
 Uo x c
Re c 
 5  105

Espessura da camada limite: d(x)
Regime laminar: Rex ≤ Rec
d( x )

x
5
Re x
Regime turbulento: Rex > Rec
d( x )
0,381

x
Re1x/ 5
5
Uo
 0
d
y
x
laminar
Regime laminar: Rex ≤ Rec

( x )
0,5  U o2
turbulento
xc

0,664
Re x
Regime turbulento: Rex > Rec
L
( x )
Tensão cisalhante na parede: (x)
0,5 
(x)
x -1 /5
U o2

0,0592
Re1x/ 5
Força na parede:
L
x -1 /2
F   ( x ) dA s   ( x ) b dx
tu r b u le n to
As
la m in a r
xc
x
0
Força de arraste: resultante da força
de superfície sobre o corpo na direção
do escoamento
6
Exemplos
Escoamento sobre Placa Plana Horizontal

Uo=cte
y
d
x


F  FD i
coeficiente de atrito
L
;
FD    s ( x) d As    s ( x) b d x   s As
S
para Rex  5 x
para 5 x
105
área de referência é As = b L
 p
 0 coeficiente de arraste
ou
 x
CD 
105
Rex 
0

s
C D  Cf L 
1
 U 2
2
1,328
Re L
CDL
Cf
107
turbulento
laminar
0,074
1740
CD 

Re1L/ 5 Re L
5 105
ReL
p
Sustentação: FL = 0
U
7
Separação da Camada Limite
p/ x=0
p/ x<0
p/ x>0
Escoamento separado
A pressão na região do escoamento
separado é baixa, devido à alta energia
cinética do escoamento naquela região
A separação altera a força de arraste
em corpos
A camada limite sempre se
separa em cantos vivos.
PUC-Rio, Angela Nieckele
8

Escoamento perpendicular a placa plana
para Re  103  FD= constante, só
depende da razão de aspecto


F  FD i
;
FD    p d A
S
O arraste é devido a diferença de
pressão a frente e atrás da placa.



Sustentação
FL=0
CD para corpos com cantos vivos são praticamente independentes de
Re porque a separação ocorre nos cantos vivos
PUC-Rio, Angela Nieckele
9

Escoamento ao redor de uma esfera ou cilindro
Nestes casos, temos arraste de pressão e viscoso.
CD 
FD
1
 V 2 Aref
2
Para baixos Re, Re < 1, não há separação e o
arraste viscoso predomina.
Lei de Stokes para Esfera
FD  3   D V
;
Ap 
 D2
4
CD 
24
Re
Para Re >10, o arraste de pressão
começa a dominar
A medida que o Reynolds cresce, o
ponto de separação se move para
montante, aumentando o arraste
de pressão.
Para 103 < Re < 105, o coeficiente
de arraste CD é praticamente
independente do no. de Reynolds.
O arraste de pressão domina. 10
Para Re <  2 x 105 o escoamento é laminar, e a separação ocorre na parte
frontal da esfera. Aumentando um pouco o número de Reynolds, o regime de
escoamento passa para turbulento e o ponto de separação move-se para
jusante, reduzindo de forma drástica a contribuição do arraste de pressão,
levando a uma queda brusca do coeficiente de arraste CD.
Obs: A rugosidade da superfície pode alterar o valor do número de Reynolds onde
ocorre a transição do escoamento laminar para turbulento, reduzindo o coeficiente
de arraste: bola de golfe
PUC-Rio, Angela Nieckele 11
CD 
FD
O escoamento ao redor de um cilindro é análogo ao
escoamento ao redor de uma esfera.
1
 V 2 Aref
2
esfera
Aref 
 D2
4
cilindro
Aref  D L
12

Escoamento ao Redor de Corpos Aerodinâmicos
O tamanho das regiões de separação atrás dos corpos pode ser
reduzida alterando-se a forma dos corpos. O objetivo na mudança
de geometria é reduzir o arraste de pressão. No entanto, ao
aumentar a área superficial o arraste viscoso cresce. Deve-se
procurar o ponto de mínimo
PUC-Rio, Angela Nieckele
13
Escoamento simétrico
FL = 0
a torna o escoamento
assimétrico  FL  0
a
V
a
FL
FL
V
a = ângulo de ataque
PUC-Rio, Angela Nieckele
14

Exemplo 1. Deseja-se colocar um tubo de pitot a 10 cm da
extremidade dianteira de um pequeno dirigível, na parte inferior. A
velocidade do dirigível varia entre 40 Km/h e 160 Km/h e a
temperatura do ar é 0 oC. Qual deve ser o comprimento da haste do
tubo de pitot?
PUC-Rio, Angela Nieckele
15

Exemplo 2. Um novo trem aerodinâmico viaja a uma velocidade
média de 172 Km/h. Calcule a potência necessária para vencer a
resistência superficial ao longo do teto e lados de um trem de 10
vagões. Os vagões possuem 25 m de comprimento; 3,4 m de largura e
4,5 m de altura. O ar está a 5 oC.
PUC-Rio, Angela Nieckele
16

Exemplo 3. Uma partícula de poeira radioativa é lançada a 10 000 m
de altitude. A densidade da partícula é de 2650 kg/m 3. Estime o tempo
de queda da partícula para as seguintes situações:
( i ) diâmetro = 10 m ( ii ) diâmetro = 1 m
PUC-Rio, Angela Nieckele
17

Exemplo 4: Uma chaminé cilíndrica de 1 m de diâmetro e 22 m de
altura está exposta a um vento uniforme de 56 km/h nas condições
atmosféricas padrão. Estime o momento fletor na base da chaminé
devido a força do vento.
PUC-Rio, Angela Nieckele
18