Testes de Hipótese Os testes de hipóteses têm como objectivo

NA PRÁTICA COMO FUNCIONA OS
TESTES DE HIPÓTESES
Testes de
Hipóteses
Não
Paramêtricos
(B)
Paramêtricos
(A)
Teste T
(1)
Teste T 2
Amostras
Independentes
(2)
Teste T 2
Amostras
Emparelhadas
(3)
Analise de
variância
[ANOVA]
(4)
Teste de
Man-Whitney
(5)
Teste do
Sina
(6)
Teste Não
Paramétrico
para Amostras
Emparelhadas
Teste de
KruskalWallis
(8)
Teste de
Wilcoxon
(7)
Testes não
paramétricos
para
proporções
Teste
Binomial
(9)
Teste do
Qui-quadrado
(10)
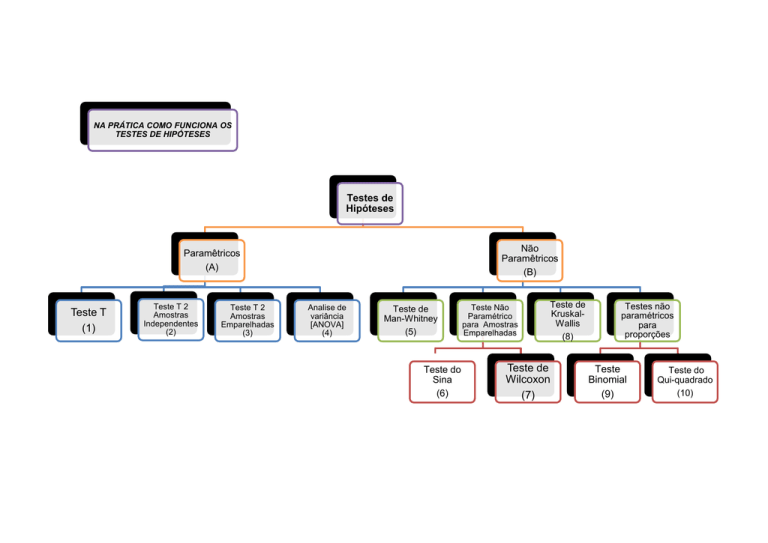
Testes de Hipótese
Os testes de hipóteses têm como objectivo decidir, com base na informação
fornecida pelos dados de uma amostra, sobre a aceitação ou não de uma dada
hipótese.
FASES DO PROCESSO:
1. Definição das hipóteses.
2. Identificação da estatística de teste e caracterização da sua distribuição.
3. Definição da regra de decisão, com especificação do nível de significância do
teste.
4. Cálculo da estatística de teste e tomada de decisão.
(A) Teste Bilateral: H0: μ = 50 H1: μ ≠ 50
(1)
condições são satisfeitas:
amostra é superior a 30 (n>30).
Skewness e Kurtosis
Teste de Kolmogorov-Smirnov (K-S):
 É um teste de aderência à Normal, isto é, testa se uma variável tem
-S:
 Se o nível de significância Sig. for inferior a um determinado valor a
então rejeitamos H0 com (1-a)*100% de confiança (normalmente a=0.05 ou
a=0.01), e rejeitamos a Normalidade.

necessário verificar a normalidade da variável.
 Se a amostra tem diemnsão inferior a 30, é necessário verificar a
normalidade da variável, por exemplo através do teste de K-S.
 Caso não se verifique a Normalidade, não se deve aplicar o teste T para
uma média, uma vez que os pressupostos não são cumpridos.
(2) Teste T para duas médias independentes
superior a 30 (n>30).
malidade:
-Smirnov (teste K-S)
(3)Teste T para duas amostras emparelhadas
antes de ler o resultado do teste-T para duas médias emparelhadas, é necessário
testar se as duas variáveis são ou não independentes.
elação para variáveis emparelhadas define o teste a utilizar:
emparelhadas é adequado.
amostras emparelhadas não é adequado.
H0:
A correlação entre as duas variáveis é nula, ou seja, as variáveis são
independentes.
H1: A correlação entre as duas variáveis não é nula, ou seja, as variáveis são
dependentes.
(4) ANOVA - Pressupostos
cada grupo é Normal
restritiva da aplicação do método
não for muito enviesada
dentes entre si
igual, o teste é robusto à não homocedasticidade (ou homogeneidade das variâncias)
-se que os grupos são de dimensão semelhante se:
não sejam verificados, temos como opção:
-Wallis)
No caso da rejeição de H0 pode ser interessante determinar qual o tratamento
que levou à rejeição
No caso de um factor ordinal:
-se a hipótese de um crescimento (ou decrescimento) de acordo
com os níveis (análise de tendência - contrastes)
-se comparações múltiplas (testes a posteriori ou post-hoc) para
determinar os grupos que diferem.
No caso de um factor nominal:
-se comparações múltiplas (testes a posteriori ou post-hoc) para
determinar os grupos que diferem.
-se grupos específicos
previamente definidos pelo investigador (testes a priori ou planeados)
Testes não paramétricos
não exigem que os dados sigam uma determinada distribuição
verificam
-se a variáveis do tipo ordinal ou superior
(5)Teste de Mann-Whitney
-se para avaliar a relação entre uma variável pelo menos ordinal com
uma dicotómica.
-Student para duas amostras independentes
quando os pressupostos do teste T não são verificados:
dimensão das amostras é pequena;
-se a normalidade dos dados a perda de eficiência do teste de
Mann- Whitney é pequena
e localização das duas amostras, em busca de diferenças
-se nas ordenações da variável, falando-se portanto em
tendência central no lugar de média.
H0: As duas populações são iguais em tendência central
H1: As duas populações não são iguais em tendência central
Testes para comparação populações emparelhadas:
(6) Teste do Sinal
-se para avaliar a relação entre uma variável pelo menos ordinal com
uma dicotómica, quando existe um critério de emparelhamento.
-se essencialmente para analisar diferenças entre pré e pós intervenção
ou tratamento.
-se no sinal da diferença dos dois momentos, não tendo em
conta o valor numérico das respostas nem da amplitude da sua diferença.
-Student para duas amostras emparelhadas
quando os pressupostos do teste T não são verificados:
-se no sinal da diferença dos dois momentos, não tendo em
conta o valor numérico das respostas nem da sua diferença:
compara as observações de acordo com o sinal de (Y – X):
aumento;
diminuição;
H0: P(+) = P(-) = ½ , isto é, a proporção de positivos é igual à proporção de
-) , isto é, a proporção de positivos é diferente da proporção
de negativos
(7)Teste de Wilcoxon
-se para avaliar a relação entre uma variável pelo menos ordinal com
uma dicotómica, quando existe um critério de emparelhamento.
-se essencialmente para analisar diferenças entre pré e pós intervenção
ou tratamento.
-Student para duas amostras emparelhadas
quando os pressupostos do teste T não são verificados:
-se nas ordens dos valores absolutos da diferença dos dois
momentos, isto é, tem em conta as amplitudes das diferenças.
-se nas ordens dos valores absolutos da diferença dos dois
momentos, tendo em conta o valor numérico das diferenças entre o “depois” e o
compara as observações de acordo com o valor absoluto de Di = |Yi –
as variáveis são ordinais ou quantitativas, o teste de Wilcoxon é mais eficiente do que
o teste do Sinal uma vez que diferenças maiores têm maior peso.
s com apenas 2 níveis, não existe diferença
entre o teste de Wilcoxon e o teste do Sinal.
A hipótese a testar é portanto:
H0: E(X) = E(Y) , isto é, o valor esperado de X é igual ao valor esperado de Y
de X não é igual ao valor esperado de
Y
(8)Teste de Kruskal-Wallis
-se para avaliar a relação entre uma variável pelo menos ordinal com
uma qualitativa com mais de dois níveis (k níveis).
-Whitney para mais de duas amostras
(assim como o One-Way-Anova generaliza o teste T para mais de duas amostras
independentes).
-Way-Anova quando os
pressupostos do One-Way-Anova não são verificados
igualdade de localização entre três ou mais amostras (k
amostras).
As hipóteses a testar são :
teste baseia-se na soma das ordens dos grupos combinados por ordem
crescente
-se o
teste exacto
-se à distribuição Qui-Quadrado com K-1 graus
de liberdade
H0: As K amostras têm o mesmo parâmetro de localização
H1: Pelo menos uma difere
Testes não paramétricos para proporções
-se a variáveis qualitativas (nominais ou ordinais) .
-se para a análise de contagens ou proporções de cada uma das
realizações ou classes das variáveis em estudo.
de mais de duas populações:
-quadrado
-Cochran
(9)Teste Binomial
amostras independentes são normalmente fruto de uma variável qualitativa nominal
dicotómica, por exemplo:
ima dos 50 anos vs
grupo abaixo dos 50 anos)
é, se a proporção no 1º grupo é igual a um determinado valor p0, por exemplo:
estar se a proporção de homens é idêntica à das mulheres (note-se que é
equivalente a testar se proporção de homens é de 0.5, teste bilateral);
-se que é
equivalente a testar se proporção de homens é superior a 0.5, teste unilateral);
inferior a 0.75.
distribuição binomial.
o no 1º grupo é igual a um determinado valor p0.
H0: p = p0 , isto é, a proporção na 1ª categoria é de p0 H1: p
proporção na 1ª categoria não é p0
H0: p ≤ p0 , isto é, a proporção na 1ª categoria não é superior a p0 H1: p > p0 ,
isto é, a proporção na 1ª categoria é superior p0
(10)Teste do Qui-Quadrado
riável qualitativa nominal com
duas ou mais categorias.
hipótese a testar é:
base na hipótese nula.
-quadrado baseia-se na comparação as frequências esperadas
com as frequências observadas em cada grupo.
-se também qui-quadrado de aderência, (goodness-of-fit) 𝜒2
H0: A variável segue uma distribuição especificada
H1: H0 é falsa
Teste do Qui-
-
Quadrado, é um caso particular e serve para testar se duas ou mais populações (ou
grupos) independentes diferem a relativamente a uma determinada característica.
-se que os grupos são normalmente resultado de uma variável qualitativa
(Por exemplo: género, faixa etária, nacionalidade, etc.)
pelas classes de uma variável nominal categorizada, é ou não idêntica.
Existe relação entre depressão e estar ou não empregado?
Existe relação entre depressão e estado civil?
Pressupostos:
Nenhuma célula da tabela tem frequência esperada inferior a 1
tem frequência esperada inferior a 5
Carlo.
duas variáveis qualitativas.
ode ser formulada da seguinte forma:
-se que H0 é equivalente a dizer que as duas variáveis em análise são
independentes, ou seja, as hipóteses podem ser formuladas das seguinte forma:
não empregado?
variável “estado civil”
H0: Não existem diferenças entre as amostras relativamente à distribuição nas
classes da variável, i.e, a distribuição das contagens pelos grupos é independente da
variável.
H1: Existem diferenças entre os grupos (ou populações de onde foram extraídas
as amostras, i.e, a distribuição das contagens pelos grupos não é independente da
variável.
H0: As variáveis em análise são independentes (ou não estão associadas). H1:
As variáveis em análise são dependentes (ou estão associadas).
Daniel Cabral
26298 CRIM