Prof - Google Groups

Prof. Mariano Vieira
CINÉTICA QUÍMICA
1. INTRODUÇÃO
As reações químicas convertem substâncias com propriedades bem definidas em
outros materiais com propriedades diferentes. É importante entender com que rapidez
essas reações ocorrem. Existem reações que se completam em frações de segundo e
ainda aquelas que levam anos para ocorrer.
A área da química que estuda a velocidade das reações é a cinética química. Na
cinética química estamos interessados nas etapas intermediárias do processo, os detalhes
das mudanças que os átomos e moléculas sofrem durante as reações.
2. FATORES QUE AFETAM A VELOCIDADE DAS REAÇÕES
Existem 4 fatores que influenciam na variação da velocidade nas quais as
reações podem ocorrer:
1) Estado físico dos reagentes: As reações ocorrem devido a choques entre as
moléculas. Quanto mais rapidamente elas se chocam, mais rápido ocorrerá a reação.
Dessa forma, líquidos e gases tendem a reagir mais rapidamente que os sólidos, que
possuem uma menor área superficial de contato.
2) Concentração dos reagentes: a maioria das reações químicas ocorrem mais
rapidamente se a concentração de um ou mais reagentes é aumentada. À medida, que a
concentração aumenta, a freqüência de choques entre as moléculas também aumenta,
ocasionando um aumento na velocidade.
3) Temperatura na qual a reação ocorre: A velocidade das reações químicas
aumenta com o aumento da temperatura. Ela aumenta a energia cinética das moléculas,
ocasionando um aumento do número de choques efetivos, aumentando assim a
velocidade das reações.
4) Presença de um catalisador: Os catalisadores são agentes que aumentam a
velocidade das reações sem serem consumidos. Eles afetam os mecanismos das colisões
que conduzem ao acontecimento das reações.
3. VELOCIDADES DAS REAÇÕES
3.1. CONCENTRAÇÃO E VELOCIDADE DE REAÇÃO
Velocidade de reação é a variação da concentração dos reagentes ou produtos
por unidade de tempo. Portanto, as unidades para velocidade de reação são geralmente
concentração em quantidade de matéria por segundo (mol.L-1.s-1).
A velocidade média de uma reação é a variação da concentração molar de um
reagente R (∆[R]) durante um certo intervalo de tempo t (∆t).
Velocidade média de desaparecimento de R = - ∆[R] / ∆t
Velocidade média de formação de P = ∆[P] / ∆t
Para uma reação genérica do tipo: aA + bB
da reação é qualquer uma das seguintes igualdades:
cC + dD, a velocidade média
Velocidade média única da reação =
3.2. VELOCIDADE INSTANTÂNEA DA REAÇÃO
A velocidade instantânea de uma reação é a inclinação
da tangente traçada no gráfico de concentração versus tempo
no instante de interesse.
Na maior parte das reações, a velocidade decresce à
medida que a reação progride.
Ex: C4H9Cl(aq) + H2O(l) → C4H9OH(aq) + HCl(aq)
Vinstantânea = ∆[C4H9Cl] / ∆t
Vinstantânea = (0,017 – 0,042) / (800 – 400)
Vinstantânea = 6,2x10-5 mol.L-1.s-1
3.3. LEIS DE VELOCIDADE E ORDEM DE REAÇÃO
As características das velocidades das reações podem ser comumente
identificadas pelo exame da velocidade inicial da reação, ou seja, a velocidade
instantânea de mudança da concentração de uma espécie no início da reação.
Uma equação que mostra como a velocidade depende das concentrações dos
reagentes é chamada de lei de velocidade e é expressa da seguinte forma:
Lei de velocidade é a expressão da velocidade instantânea de reação em termos
da concentração de uma espécie em qualquer instante. Cada reação tem sua própria lei
de velocidade.
A constante de velocidade k é característica e independe das concentrações dos
reagentes, mas depende da temperatura e da presença de um catalisador.
Quando o expoente da potência na equação da lei de velocidade (m) é igual a 1
dizemos que a reação é de primeira ordem, quando m é igual a 2 a reação é dita de
segunda ordem.
Há casos em que a velocidade não depende da concentração e dizemos que a
reação é de ordem zero. Um exemplo deste caso é a reação de decomposição da amônia,
cuja lei de velocidade é expressa da seguinte maneira:
2NH3(g)
N2(g) + 3H2(g)
vNH3 = k
Uma lei de velocidade é uma lei empírica. É determinada experimentalmente e
não pode, em geral, ser escrita a partir da estequiometria da equação química da reação.
Portanto, a ordem total da reação é a soma dos expoentes (m + n) da equação da lei de
velocidade.
Os expoentes em uma lei de velocidade indicam como a velocidade é afetada
pela concentração de cada reagente. Se dobrarmos a concentração de um reagente em
uma reação de primeira ordem, a velocidade de reação dobra. Dobrando a concentração
de um reagente em uma reação de segunda ordem, a velocidade de reação aumenta por
um fator de 22 = 4.
As ordens podem ser números negativos. Uma ordem negativa significa que a
concentração aparece no denominador da lei de velocidade.
Quando transformamos uma reação de segunda ordem em uma reação de
pseudo-primeira ordem uma nova constante k’ é apresentada.
Ex: Reação de 2° ordem: vS8O82- = k [S8O82-].[I-]
Se [S8O82-] for constante no começo e final da reação, temos:
Reação de 1° ordem: vS8O82- = k’ [I-], onde k’ = k [S8O82-]
Uma lei de velocidade de uma reação de pseudo-primeira ordem é muito mais
fácil de analisar do que a velocidade verdadeira, porque sua velocidade depende
somente de uma substância.
3.4. CONCENTRAÇÃO E TEMPO
Uma lei de velocidade integrada dá a concentração de reagentes ou produtos em
qualquer instante após o início da reação.
3.4.1. LEIS DE VELOCIDADES INTEGRADAS DE 1° ORDEM
Uma reação de primeira ordem é aquela cuja velocidade depende da
concentração de um único reagente elevada a primeira potência.
Para uma reação de primeira ordem, a lei de velocidade pode ser expressa da
seguinte forma:
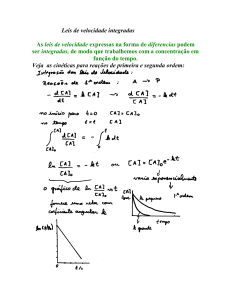
ln[A]t/[A]0=-kt
ou
[A]t=[A]0e-kt
O gráfico da variação de
concentração com o tempo predito
pela equação acima mostra o
comportamento
chamado
de
decaimento exponencial. A variação
de concentração é inicialmente rápida
e torna-se mais lenta à medida que o
reagente é consumido.
Para verificar se uma reação é de primeira ordem, lançamos em gráfico o
logaritmo natural em função do tempo. Se obtivermos uma reta, a reação é de primeira
ordem e a inclinação do gráfico é - k.
3.4.2. MEIA-VIDA DE REAÇÕES DE PRIMEIRA ORDEM
A meia-vida de uma reação é o tempo necessário para que sua concentração caia
pela metade do valor inicial.
Para uma reação de 1° ordem temos:
ln [A]t / [A]0 = - kt
ln 1/2[A]0 / [A]0 = - kt1/2
t1/2 = -ln 1/2 / k
ou
t1/2 = ln 2 / k
Pela equação, a meia-vida de uma reação de primeira ordem só depende de k
logo, não é afetada pela concentração inicial dos reagentes. Nas reações em que k é
grande a meia-vida será curta.
O conceito de meia-vida é muito utilizado para descrever o decaimento
radioativo, que é um processo de primeira ordem.
3.4.3. LEIS DE VELOCIDADES INTEGRADAS DE SEGUNDA ORDEM
Uma reação de segunda ordem é aquela cuja velocidade depende da
concentração do reagente elevado a segunda potência ou da concentração de dois
reagentes diferentes, cada um elevado a primeira potência.
Para uma reação de segunda ordem, expressamos a lei de velocidade como:
1/[A]t = kt + 1/[A]0
O gráfico da variação de
concentração versus tempo mostra que a
concentração do reagente decresce
rapidamente no princípio, e depois, muda
mais lentamente do que uma reação de
primeira ordem com a mesma velocidade
inicial.
Para determinar se uma reação é de segunda ordem, lançamos em gráfico o
inverso da concentração em função do tempo, para ver se o resultado é uma reta. A
inclinação da reta é k.
A meia-vida de uma reação de segunda ordem depende de k e da [A]0.
t1/2 = ln 2 / k . [A]0
4. MECANISMOS DE REAÇÃO
4.1. REAÇÕES ELEMENTARES
Não podemos, em geral, escrever uma lei de velocidade a partir de uma equação
química. A razão é que todas as reações, com exceto a mais simples, são o resultado de
várias, e, às vezes, muitas etapas chamadas de reações elementares. Cada reação
elementar descreve um evento distinto, com freqüência, uma colisão de partículas.
Para entender como uma reação se desenvolve, temos que propor um mecanismo
de reação, isto é, uma seqüência de reações elementares que descreve as modificações
que acreditamos que ocorram à medida que os reagentes se transformam em produtos.
Um mecanismo de reação é um modelo característico de cada reação.
Vários mecanismos podem ser propostos para uma reação e medidas da
velocidade são usadas para decidir qual é o mecanismo mais provável.
Existem espécies que desempenham uma função na reação, mas que não
aparecem na equação química da reação total. Essas espécies são chamadas
intermediários e são produzidas durante uma etapa e consumidos em outra.
As equações elementares são resumidas por equações químicas escritas sem os
símbolos de estado.
Ex: O3
O2 + O
O número de moléculas que participam como reagentes em uma etapa elementar
definem a molecularidade.
Uma reação unimolecular é a reação em que apenas uma molécula de um
reagente está envolvida. Reação bimolecular é a reação em que duas moléculas se
encontram e reagem. Quando mais de duas moléculas de reagente participam da reação
dizemos que ela é termolecular.
Não usamos coeficientes estequiométricos nas reações elementares, ao contrário,
escrevemos as fórmulas quantas vezes forem necessárias. Também não se especifica o
estado das espécies, porque a equação tem como objetivo mostrar que um único átomo
colide com outra molécula.
4.2. LEIS DE VELOCIDADE DAS REAÇÕES ELEMENTARES
Para verificar se um mecanismo proposto concorda com os dados experimentais,
é necessário construir a lei de velocidade determinada experimentalmente. Embora a lei
de velocidade calculada e experimental possam ser as mesmas, o mecanismo proposto
pode não ser o correto, porque outros mecanismos também podem levar à mesma lei de
velocidade.
As informações cinéticas podem somente apoiar um mecanismo proposto. Elas
não podem nunca provar que um mecanismo é correto.
A primeira tarefa na construção de uma lei de velocidade total de um mecanismo
é escrever as leis de velocidades das reações elementares propostas. A segunda, é
combiná-las a uma lei de velocidade total.
A etapa determinante da velocidade de reação é a etapa lenta que controla a
velocidade de formação total dos produtos.
4.3. REAÇÕES EM CADEIA
As reações que ocorrem com velocidade explosiva são, com freqüência, reações
em cadeia. Em uma reação em cadeia, um intermediário muito reativo reage para
produzir outro intermediário muito reativo, e assim por diante.
O intermediário de reação, que nesse contexto é chamado de propagador de
cadeia, é um radical e a reação é chamada de reação em cadeia via radicais.
A primeira etapa de qualquer reação em cadeia é a iniciação, a formação de
propagadores de cadeia a partir de um reagente. Calor ou luz são geralmente usados
para gerar os propagadores de cadeia.
Ex:
Br2
luz
Br
Br
Uma vez formado os propagadores (radicais), a cadeia se propaga, isto é, um
propagador reage com uma molécula do reagente para produzir outro propagador.
Ex:
Br
H2
HBr
H
H
Br2
HBr
Br
A reação elementar que termina a cadeia, num processo chamado terminação,
ocorre quando dois propagadores se combinam para formar produtos.
Ex:
Br
H
Br
Br
Br2
HBr
5. MODELOS DE REAÇÃO
5.1. EFEITO DA TEMPERATURA
Muitas reações acontecem mais rapidamente quando a temperatura aumenta. No
final do século XIX, o químico sueco Arrhenius descobriu que o gráfico do logaritmo
natural da constante de velocidade (k) contra o inverso da temperatura absoluta é uma
linha reta. Dizemos que as reações que obedecem a equação abaixo, possuem
comportamento de Arrhenius.
ln k = ln A – Ea/RT onde:
A – é o fator pré-exponencial ou fator de frequência
Ea – é a energia de ativação
A e Ea são conhecidos como parâmetros de Arrhenius. Ambos são determinados
experimentalmente e são praticamente independentes da temperatura, mas dependem da
reação que está sendo estudada.
Na equação de Arrhenius quanto maior for a Ea, maior será a variação da
constante de velocidade (k) com a temperatura. Ea é baixa para valores próximos a 10 kJ
e acima de 60 kJ é considerada alta.
Algumas reações espontâneas não ocorrem porque tem Ea muito alta. A variação
da constante de velocidade com a temperatura e sua sensibilidade a energia de ativação,
juntamente com a relação Keq = k / k’, explicam a dependência da constante de
equilíbrio com a temperatura.
Usamos diagramas conhecidos como perfis de
reação para representar as variações de energia que
ocorrem durante uma reação.
A energia de ativação de uma reação endotérmica é
maior na direção direta que na inversa, de modo que a
velocidade da reação direta é mais sensível à temperatura,
e o equilíbrio se desloca para os produtos quando a
temperatura aumenta (Keq > 1). O oposto é verdadeiro para uma reação exotérmica e a
reação inversa é mais sensível à temperatura. Nesse caso, o equilíbrio se desloca na
direção dos reagentes, quando T aumenta (Keq < 1).
Uma maneira de calcular a energia de ativação é rearranjando a equação de
Arrhenius como abaixo:
ln k’ / k = Ea/R (1/T – 1/T’)
5.2. TEORIA DE COLISÕES
Nesse modelo, supomos que as moléculas se comportam como bolas de bilhar
defeituosas: quando elas colidem em velocidades baixas, elas ricocheteiam, mas podem
se despedaçar quando o impacto tem energia muito alta. Se duas moléculas colidem
com energia cinética abaixo de certo valor, elas simplesmente ricocheteiam. Se elas se
encontram com energia maior que esse valor, ligações químicas podem se quebrar e
novas ligações podem se formar.
Para estabelecer uma teoria quantitativa baseada nessa representação qualitativa,
é preciso saber a freqüência com que as moléculas colidem e as frações das colisões,
que tem pelo menos a energia mínima (Emin):
Frequência de colisão = σ . νrel . NA2 . [A].[B] , onde NA é a constante de Avogadro.
Utilizando a distribuição das velocidades de Maxwell e a equação de Arrhenius
chegamos à seguinte equação para o modelo de colisões:
ln K = ln (σ . νrel . NA2) – Ea/RT , onde A é a medida da velocidade com que as
moléculas colidem e Ea é a energia cinética mínima necessária para que uma colisão
resulte em reação.
Resultados experimentais mostraram incoerência no modelo, sendo necessário
reformulação da teoria de colisão. À equação foi introduzido um fator empírico, P,
chamado de exigência estérica. A nova equação leva em conta a freqüência de colisão,
sua energia cinética e a exigência estérica.
K = P (σ . νrel . NA2) . e -Ea/RT
5.3. TEORIA DO COMPLEXO ATIVADO
Uma teoria mais geral, que explica as reações em solução, e também se aplica a
reações em fase gasosa, é chamada de teoria do complexo ativado.
Essa teoria aperfeiçoa a teoria das colisões ao sugerir um modo de calcular a
constante de velocidade mesmo quando as exigências estéricas são significativas. Nessa
teoria, imaginamos que duas moléculas se aproximam e se deformam quando se
encontram. Na fase gasosa, o encontro e a deformação equivalem-se a colisão da teoria
das colisões. Em solução, a aproximação é uma trajetória em zig-zag entre moléculas de
solvente, e a deformação pode não ocorrer até que as duas moléculas reagentes tenham
se encontrado e recebido um “chute” particularmente rigoroso das moléculas do
solvente que estão ao redor.
Nos dois casos, a colisão ou o “chute” não desfazem as moléculas
imediatamente. Em vez disso, o encontro leva a formação de um complexo ativado, um
arranjo das duas moléculas que pode prosseguir na direção dos produtos ou se separar
para restabelecer os reagentes não modificados. No complexo ativado, as ligações
originais se esticaram e enfraqueceram, e as novas ligações estão parcialmente
formadas.
Na teoria do complexo ativado, a energia de ativação é uma medida da energia
do complexo ativado em relação a dos
reagentes.
Observações do gráfico:
1)
A energia potencial total varia à
medida que os reagentes se aproximam, se
encontram, formam o complexo ativado e prosseguem na direção dos produtos.
2)
Quando os reagentes se aproximam eles perdem energia cinética e sobem o lado
esquerdo da barreira.
3)
Se os reagentes têm energia cinética menor do que Ea quando estão muito
afastados, eles não atingem o topo da barreira de potencial e “rolam” de volta pelo lado
esquerdo, separando-se.
4)
Se eles têm energia cinética mínima de Ea quando estão muito afastados, eles
podem formar o complexo ativado, passar o topo da barreira e “rolar” pelo outro lado,
onde se separam como produtos.
Em resumo, na teria do complexo ativado, uma reação só ocorre se duas
moléculas adquirem energia suficiente, talvez do solvente ao redor, para formar um
complexo ativado e atravessar uma barreira energética.
6. ACELERAÇÃO DAS REAÇÕES
6.1. CATÁLISE
Um modo de aumentar a velocidade de
uma reação é usar um catalisador, substância
que aumenta a velocidade sem ser consumida
na reação.
Um catalisador acelera uma reação
fornecendo um caminho alternativo – um
mecanismo de reação diferente – entre
reagentes e produtos. Esse novo caminho tem
energia de ativação mais baixa do que o
caminho original.
Embora a reação ocorra rapidamente, o catalisador não afeta a composição do
equilíbrio.
6.1.1. CATÁLISE HOMOGÊNEA
Um catalisador homogêneo é aquele que está na mesma fase dos reagentes.
Apesar de um catalisador não aparecer na equação balanceada de uma equação, a
concentração de um catalisador homogêneo aparece na lei de velocidade.
6.1.2. CATÁLISE HETEROGÊNEA
Um catalisador heterogêneo é aquele que está numa fase diferente das dos
reagentes. Os mais comuns são sólidos finamente divididos ou porosos, usados em
reações de fase gasosa ou líquida. São encontrados dessa forma para aumentar a
superfície de contato.
Os catalisadores podem ser envenenados ou inativos. Uma causa comum de
envenenamento é a adsorção de uma molécula tão fortemente ao catalisador que ela sela
sua superfície para as reações posteriores.
6.2. CATALISADORES VIVOS: ENZIMAS
As células vivas contém milhares de tipos diferentes de catalisadores, cada um
dos quais é necessário à vida. Muitos desses catalisadores são proteínas chamadas
enzimas. Essas proteínas são moléculas muito grandes que tem um sítio ativo
semelhante a uma cavidade como uma chave que se encaixa em uma fechadura. No
entanto, ao contrário de uma fechadura comum, a molécula de proteína se distorce
ligeiramente quando uma molécula de substrato se aproxima e sua capacidade em
realizar distorção correta também determina se a chave irá servir. Esse refinamento do
modelo original chave-fechadura é conhecido como mecanismo de ajuste induzido da
ação enzimática.
Uma vez no sítio ativo, o substrato reage. O produto é liberado para uso na etapa
seguinte, que é controlada por outra enzima, e a molécula da enzima original fica livre
para receber a próxima molécula do substrato.
A cinética das reações enzimáticas foi estudada pela primeira vez pelos químicos
alemães Michaelis e Menten, no início do século XX. Eles propuseram a lei de
velocidade de formação do produto: V = (k2.[E0].[S])/ KM+[S], onde: KM é a constante
de Michaelis, KM = (k1’ + k2) / k1