Lista de exercícios – Trigonometria

1
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
MATEMÁTICA, LICENCIATURA
Matemática Elementar: Unidade 8 – “Os seres matemáticos são seres sociais” /Quest(i)
Prof. Lucas Nunes Ogliari
[07/10/2014]
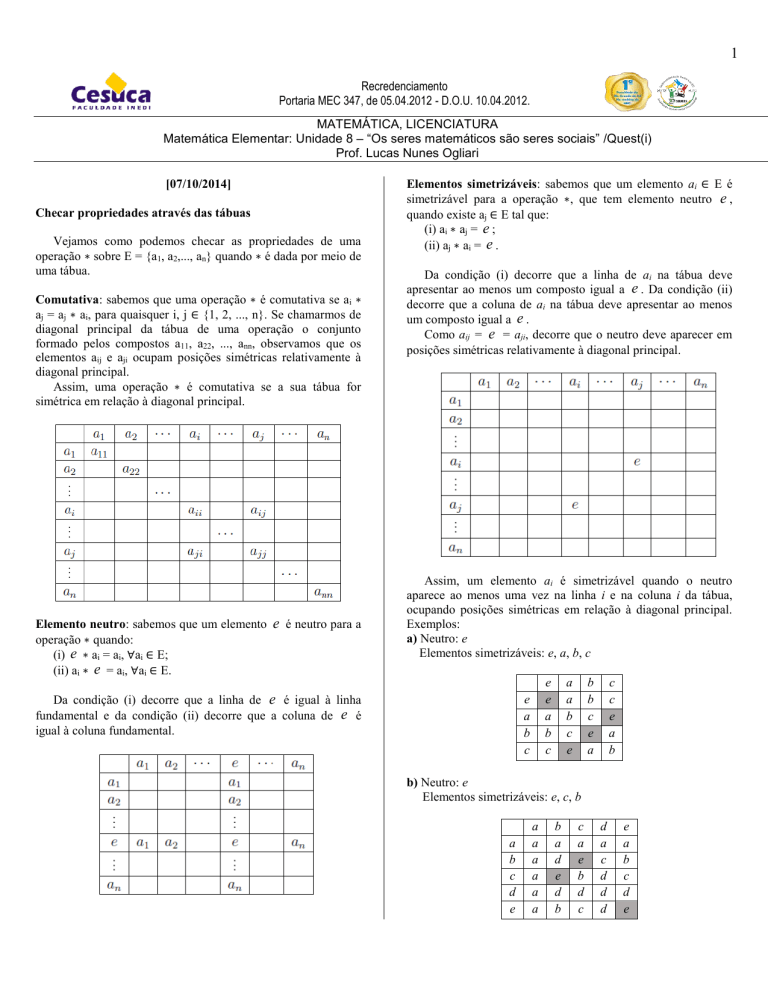
Checar propriedades através das tábuas
Vejamos como podemos checar as propriedades de uma
operação ∗ sobre E = {a1, a2,..., an} quando ∗ é dada por meio de
uma tábua.
Comutativa: sabemos que uma operação ∗ é comutativa se ai ∗
aj = aj ∗ ai, para quaisquer i, j ∈ {1, 2, ..., n}. Se chamarmos de
diagonal principal da tábua de uma operação o conjunto
formado pelos compostos a11, a22, ..., ann, observamos que os
elementos aij e aji ocupam posições simétricas relativamente à
diagonal principal.
Assim, uma operação ∗ é comutativa se a sua tábua for
simétrica em relação à diagonal principal.
Elemento neutro: sabemos que um elemento
operação ∗ quando:
(i) e ∗ ai = ai, ∀ai ∈ E;
(ii) ai ∗ e = ai, ∀ai ∈ E.
e é neutro para a
Elementos simetrizáveis: sabemos que um elemento ai ∈ E é
simetrizável para a operação ∗, que tem elemento neutro e ,
quando existe aj ∈ E tal que:
(i) ai ∗ aj = e ;
(ii) aj ∗ ai = e .
Da condição (i) decorre que a linha de ai na tábua deve
apresentar ao menos um composto igual a e . Da condição (ii)
decorre que a coluna de ai na tábua deve apresentar ao menos
um composto igual a e .
Como aij = e = aji, decorre que o neutro deve aparecer em
posições simétricas relativamente à diagonal principal.
Assim, um elemento ai é simetrizável quando o neutro
aparece ao menos uma vez na linha i e na coluna i da tábua,
ocupando posições simétricas em relação à diagonal principal.
Exemplos:
a) Neutro: e
Elementos simetrizáveis: e, a, b, c
Da condição (i) decorre que a linha de e é igual à linha
fundamental e da condição (ii) decorre que a coluna de e é
igual à coluna fundamental.
e
e
a
b
c
e
a
b
c
a
a
b
c
e
b
b
c
e
a
c
c
e
a
b
b) Neutro: e
Elementos simetrizáveis: e, c, b
a
b
c
d
e
a
a
a
a
a
a
b
a
d
e
d
b
c
a
e
b
d
c
d
a
c
d
d
d
e
a
b
c
d
e
2
Elementos regulares: sabemos que um elemento a ∈ E é
regular em relação à operação ∗ quando:
(i) a ∗ ai  a ∗ aj , sempre que ai  aj;
(ii) ai ∗ a  aj ∗ a, sempre que ai  aj.
Isso significa que a é regular quando, composto com
elementos distintos de E, tanto à esquerda deles como à direita,
produz resultados diferentes. Assim, um elemento a é regular
quando na linha e na coluna de a não há elementos iguais. Por
exemplo, considerando a operação cuja tábua é dada abaixo, são
os elementos regulares: e, a, d. Note que na linha e coluna de b
ocorrem repetições, e na de c também.
Exercícios
1) Construa a tábua de intersecção sobre a família de conjuntos
F = {A, B, C, D}, sabendo-se que:
A  B  B, B  C  C e C  D  D

A
B
C
D
A
B
C
D
A
B
C
D
B
B
C
D
C
C
C
D
D
D
D
D
Em seguida, estabeleça:
a) Qual é o elemento neutro; A
b) Que elementos são simetrizáveis; A
c) Que elementos são regulares. A
Outros exemplos
2) A partir de cada tábua abaixo, decida:
1) Complete a tábua abaixo de modo que ela defina uma
operação comutativa * sobre o conjunto A = {1,2,3,4}:
i) A operação é comutativa?
a) e c)
*
1
2
3
4
1
1
2
3
4
2
2
4
1
3
3
3
1
4
2
ii) Existe elementos neutro? Qual?
a) elemento neutro c.
b) elemento neutro b.
c) elemento neutro a.
4
4
3
2
1
2) Seja o grupóide ({1,2,3}, *) , a operação * sendo definida
pela tábua abaixo:
*
1
2
3
1
2
3
1
2
3
1
2
iii) Que elementos são simetrizáveis?
a) todos.
b) b.
c) todos.
iv) Que elementos são regulares?
a) todos
b) a, b.
c) todos.
3
1
2
3
a)
Determine o elemento neutro. R: 3
3) Dadas as tábuas abaixo com operações sobre A = {1,2,3}:

1
2
3
1
1
2
3
2
2
1
1
3
3
1
1

1
2
3
1
1
2
3
2
2
2
1
3
3
1
2
Determine:
a) O elemento neutro de cada uma das operações. Em relação às
duas operações o elemento neutro é 1.
b) Os elementos simetrizáveis do grupóide (A,  ). Todos.
b)
c)
3
3) Monte a tábua da operação * sobre o conjunto E = {a, b, c,
d}, sabendo-se que:
(I)
(II)
(III)
(IV)
(V)
b é elemento neutro
o simétrico de a é a
o simétrico de c é d
a*c = d
todos os elementos de E são regulares
*
a
b
c
d
a
b
a
d
c
b
a
b
c
d
c
d
c
a
b
d
c
d
b
a
4) Seja * a operação sobre E = {1, 2, 3, 4, 6, 12} dada pela lei
x * y  mmc( x, y ) . Determine os subconjuntos de E que tem
três elementos e são fechados em relação a essa operação.
*
1
2
3
4
6
12
1
1
2
3
4
6
12
2
2
2
6
4
6
12
3
3
6
3
12
6
12
4
4
4
12
4
12
12
6
6
6
6
12
6
12
12
12
12
12
12
12
12
{1, 2, 4} {1, 2, 6} {1, 2, 12} {1, 3, 6} {1, 3, 12} {1, 4, 12} {1,
6, 12} {2, 3, 6} {2, 4, 12} {2, 6, 12} {3, 4, 12} {3, 6, 12} {4, 6,
12}
5) Complete a tábua de operações * sobre E = {a, b, c, d, e},
sabendo que:
(I)
(II)
(III)
(IV)
(V)
e*x = x = x*e, x
a*x = a = x*a, x
x*x = e, x  a
b*d = c
b, c, d são regulares
*
a
b
c
d
e
a
a
a
a
a
a
b
a
e
d
c
b
c
a
d
e
b
c
d
a
c
b
e
d
e
a
b
c
d
e
(VI)