Exame de Conhecimentos em F´ısica

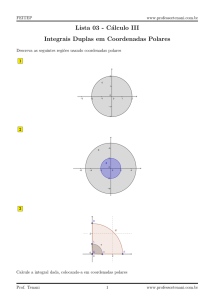
Programa de Pós-Graduação
Processo de Seleção − 1o Semestre de 2012
Exame de Conhecimentos em Fı́sica
Candidato(a):
Curso:
Mestrado
Doutorado
Observações:
• O Exame de Conhecimentos em Fı́sica consiste em 20 questões objetivas.
• O nome completo e a modalidade (Mestrado ou Doutorado) do(a) candidato(a) devem
ser assinalados nos campos correspondentes, na capa e na Folha de Respostas do Exame.
• As respostas devem ser transcritas, à caneta, para a Folha de Respostas, sem rasuras.
• Em todas as questões, apenas uma alternativa é correta. Marque apenas uma alternativa para cada questão na Folha de Respostas.
• 3 (três) questões assinaladas incorretamente anulam uma questão assinalada
corretamente.
1) Um corpo com massa m é lançado para baixo sobre a água com velocidade inicial igual a
v0 = 3mg
k , onde k é um coeficiente de proporcionalidade da força de resistência do movimento
deste corpo na água, FR = kv, sendo v a velocidade unidimensional do corpo. A equação da
velocidade do corpo é dada por:
(
+ e− m
kt
(a) v(t) =
2mg
k
(b) v(t) =
3mg
k
(c) v(t) =
2mg − kt
m
k e
(d) v(t) =
3mg
k
(e) v(t) =
2mg
k
(
(
(
1
2
1 + e− m
)
2kt
1
2
− e− m
1
2
− e− m
kt
kt
)
)
)
2) Uma mola, que não obedece à Lei de Hooke, ao ser comprimida ou esticada exerce uma força
restauradora dada por: F (x) = −αx − βx2 . Uma partı́cula com massa m é presa à mola no
ponto em que há uma distensão de δx1 com relação ao ponto de equilı́brio inicial. Escolha a
alternativa correta:
(a) Este sistema é não conservativo, define-se a função energia potencial associada que é
dada por U (x) = −α − 2βx. O ponto x = − αβ é um ponto de equilı́brio estável global.
(b) Este sistema é não conservativo, define-se a função energia potencial associada que é
dada por U (x) = α2 x2 + β3 x3 . O ponto x = − αβ é um ponto de equilı́brio estável local.
(c) Este sistema é não conservativo, define-se a função energia potencial associada que é
α
dada por U (x) = − α2 x2 − β3 x3 . O ponto x = − 2β
é um ponto de equilı́brio estável local.
(d) Este sistema é conservativo, define-se a função energia potencial associada que é dada
α
por U (x) = α2 x2 + β3 x3 . O ponto x = − 2β
é um ponto de equilı́brio estável global.
(e) Este sistema é não conservativo, define-se a energia potencial associada que é dada
por U (x) = α + 2βx. O ponto x = − αβ é um ponto de equilı́brio estável local.
2
3) Um cilindro desliza ao longo de uma superfı́cie horizontal sujeito a uma força de atrito com
coeficiente de atrito cinético µc até começar a rolar. Considerando que o momento de inércia
2
do cilindro é I = M2R , e que a partir de um certo momento ele passa a rolar, sabemos que:
(a) A aceleração inicial do centro de massa é dada por a = µc g, a aceleração angular do
cilindro assim que ele começa a rolar é α = µRc g .
(b) A aceleração inicial do centro de massa é dada por a = 2µc g, a aceleração angular
do cilindro assim que ele começa a rolar é α = µRc g .
(c) A aceleração inicial do centro de massa é dada por a = 2µc g, a aceleração angular do
cilindro assim que ele começa a rolar é α = 2µRc g .
(d) A aceleração inicial do centro de massa é dada por a = µc g, a aceleração angular do
cilindro assim que ele começa a rolar é α = 2µRc g .
(e) A aceleração inicial do centro de massa é dada por a = µc g, a aceleração angular do
cg
cilindro assim que ele começa a rolar é α = µ2R
.
4) Dado o seguinte Lagrangeano: L = eλt
podemos afirmar que:
(
mẋ2
2
−
k2 x 2
2
)
− mgx , utilizando a notação
dx
dt
= ẋ,
(a) Este sistema é conservativo e que a equação de Euler Lagrange é dada por:
eλt ẍ + eλt λẋ + g +
k2
x = 0.
m
(b) Este sistema é não conservativo e que a equação de Euler Lagrange é dada por:
eλt ẍ + eλt λẋ − g −
k2
x = 0.
m
(c) Este sistema é conservativo e que a equação de Euler Lagrange é dada por:
mẍ + mλẋ + gm + k2 x = 0.
(d) Este sistema é não conservativo e que a equação de Euler Lagrange é dada por:
ẍ + λeλt ẋ − g −
k2
x = 0.
m
(e) Este sistema é não conservativo e que a equação de Euler Lagrange é dada por:
ẍ + λẋ + g +
3
k2
x = 0.
m
5) Um fio de 40 cm é utilizado para segurar uma bola de massa M = 1 kg em movimento circular uniforme inicialmente em uma circunferência de raio R0 = 20 cm a velocidade v0 = 2 m/s.
A outra metade deste fio inicialmente passa por um tubo perpendicular ao plano de rotação e
torna possı́vel puxar a bola para rodar em uma circunferência de R1 = 10 cm de raio ao aplicar
uma força F durante 2 segundos. A força F aplicada tem intensidade de:
(a) 12 N
(b) 10 N
(c) 60 N
(d) 6 N
Formulário:
d
dt
d
dt
(
(
∂L
∂ q̇i
∂L
∂ q̇i
)
−
∂L
=0
∂qi
−
∂L ∑
λi qi,k
=
∂qi
)
N
k
∂U
d
qi = −
+
∂qi
dt
4
(
∂U
∂ q̇i
)
(e) 36 N
6) Considere o modelo atômico de Thomson que consiste em uma esfera de raio R com carga
+e uniformemente distribuı́da em seu volume e uma partı́cula puntiforme (o elétron) de massa
m e carga −e. Quais afirmativas abaixo estão corretas?
I) Dentro da esfera o elétron está submetido a um potencial harmônico.
II) Fora da esfera o potencial sentido pelo elétron é harmônico.
III) O único ponto de equilı́brio para o elétron é no centro da esfera.
IV) O elétron estará em equilı́brio em qualquer lugar dentro da esfera.
(a) I e II
(b) I e III
(c) I e IV
(d) II e III
(e) II e IV
7) Suponha que um campo magnético uniforme e paralelo ao eixo z se estenda por todo o espaço
e seja dado pela forma B = (−B0 t/r)k, onde t é o tempo e r é a distância do ponto considerado
ao eixo z. Nessas condições é correto afirmar que:
(a) Não haverá campo elétrico induzido.
(b) Haverá campo elétrico induzido e ele cai como 1/r.
(c) Haverá campo elétrico induzido e ele é uniforme na direção y.
(d) Haverá campo elétrico induzido de magnitude constante.
(e) Haverá campo elétrico induzido apenas no interior de uma espira condutora.
8) Um feixe de prótons se move a uma velocidade constante de 1,2 km/s e entra numa região
onde há um campo magnético uniforme, constante e paralelo ao eixo z. Considerando que
eventuais emissões de radiação pelos prótons sejam desprezı́veis, quais das afirmações abaixo
NÃO estão corretas:
I) Após sair da região de campo, a velocidade dos prótons será maior que 1,2 km/s.
II) Após sair da região de campo, a velocidade dos prótons será menor que 1,2 km/s.
III) Se o feixe entra na região de campo na direção x, percorre 1,18 cm perfazendo um
quarto de circunferência, e sai da região de campo na direção y, então a magnitude do campo
magnético é 0,167 T.
(a) Apenas I
(b) Apenas I e II
(c) Apenas I e III
5
(d) Apenas II e III
(e) Todas
9) Um condutor possui a forma de um clilindro oco muito longo de raio interno a e raio externo
b. Ele conduz uma corrente I uniformemente distribuı́da ao longo de sua seção reta. Sendo r a
distância de um ponto qualquer ao eixo do cilindro, quais dentre as afirmativas a seguir estão
corretas?
I) Para r < a, o campo magnético é constante e não nulo.
II) Para a < r < b, o campo magnético é proporcional a (r2 − a2 )/r.
III) Para r > b, o campo magnético tem magnitude µ0 I/2πr.
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) I e II
(e) II e III
10) Uma haste metálica fina, de comprimento igual a 0,24 m gira com velocidade angular de 8,8
rad/s em torno de um eixo perpendicular à haste que passa por uma de suas extremidades. O
plano de rotação da haste é perpendicular a um campo magnético uniforme com módulo igual
a 0,65 T. A diferença de potencial entre as extremidades da haste é:
(a) 0,16 V
(b) 0,6 V
(c) 0,016 V
(d) 2,4 V
Formulário:
I
q
E · dA =
ϵ0
S
I
∫
E · dl = −
C
S
∂B
· dA
∂t
I
B · dA = 0
S
I
∫
B · dl = µ0 I + µ0 ϵ0
C
S
∂E
· dA
∂t
F = q(E + v × B)
me = 9, 1 × 10−31 kg
e = 1, 6 × 10−19 C
mp = 1, 67 × 10−27 kg
ϵ0 = 8, 85 × 10−12 C2 /N · m2
6
(e) 1,2 V
11) A distância entre o primeiro e o quinto mı́nimo de uma figura de difração de uma fenda é
0,35 mm, com a tela a 40 cm de distância da fenda, quando é usada uma luz com um comprimento de onda de 550 nm. Com esses parâmetros a largura da fenda é:
(a) 2,5 mm
(b) 2,5 µm
(c) 25 mm
(d) 25 µm
(e) 2,5 nm
12) Em um experimento de interferência de dupla fenda com luz monocromática, as franjas
são obtidas numa tela colocada a uma distância D das fendas. Se a tela é movida de 5 cm em
direção às fendas, é produzida uma mudança na largura das franjas de 30 µm. Se a distância
entre as fendas é de 1 mm então o comprimento de onda da luz usada no experimento é de:
(a) 4000 Å
(b) 5328 Å
(c) 5890 Å
(d) 8000 Å
(e) 6000 Å
13) Considere um conjunto de funções de onda Ψi (x). Qual das seguintes condições garante
que as funções são normalizadas e ortogonais? (Os ı́ndices i e j tem valores 1, 2, ... , n).
(a) Ψ∗i (x)Ψj (x) = 0
(d)
∫∞
∗
−∞ Ψi (x)Ψj (x)dx = 1
(b) Ψ∗i (x)Ψj (x) = 1
(e)
∫∞
∗
−∞ Ψi (x)Ψj (x)dx
7
(c)
= δij
∫∞
∗
−∞ Ψi (x)Ψj (x)dx
=0
14) Considere uma partı́cula de massa m confinada entre os pontos x = −a/2 e x = +a/2, que
pode se mover livremente nesta região ao longo do eixo x. Suponha que as paredes que limitam
esta região sejam completamente impenetráveis (poço de potencial infinito unidimensional) e a
partı́cula está submetida a um potencial nulo. Para o estado de menor energia da partı́cula a
função de onda é dada por

( )
 A cos πx e−iEt/~ ,
a
Ψ=

0,
−a/2 < x < a/2
x < −a/2,
x > a/2
onde A é uma constante real e E é a energia total para este estado. O valor esperado de p2 é:
[
(a) 0
(b) 2π
a
]−2 [
]
π −1
6
2
[
(c) ~π
a
(d) ~π
a
√
(
]2
(e)
2π
a
)−2 (
π2 − 1
6
)
15) Qual ou quais das seguintes caracterı́sticas são de um oscilador harmônico quântico unidimensional?
I) Um espectro de estados de energia, uniformemente espaçados.
II) Uma função de energia potencial que é linear na coordenada de posição.
III) Um estado fundamental que é caracterizado por ter energia cinética igual a zero.
IV) Uma probabilidade não-nula de encontrar o oscilador nos pontos de retorno.
(a) Apenas I
(b) Apenas IV
(c) Apenas I e IV
8
(d) Apenas II e III
(e) Todas
16) Em um episódio de gripe, um homem de 80 kg tem sua temperatura elevada de 2 ◦ C,
chegando a 39 ◦ C de febre. Sabendo que calor especı́fico do corpo humano é 3480 J/kg·K, a
quantidade necessária de calor para produzir essa variação de temperatura é:
(a) 133 kcal
(b) 143 kcal
(c) 153 kcal
(d) 163 kcal
(e) 173 kcal
17) A variação da pressão atmosférica com a altura H na atmosfera terrestre, supondo que a
temperatura T , a composição quı́mica (i.e., a mesma massa molar M ) e a gravidade g permaneçam constantes em todas as altitudes é:
(a) P = P0 ln(M gH/RT )
(b) P = P0 ln(RT /mgH)
(c) P = P0 exp(M gH/RT )
(d) P = −P0 exp(M gH/RT )
(e) P = P0 exp(−M gH/RT )
18) A função f que descreve a distribuição real das velocidades moleculares denomina-se distribuição de Maxwell-Boltzman:
f (v) = 4π
( m )3/2
2
v 2 e−mv /2kT .
2πkT
Em termos da energia cinética translacional ϵ de uma única molécula essa função pode ser
escrita como
8π ( m )3/2 −ϵ/kT
f (ϵ) =
ϵe
.
m 2πkT
O pico de cada curva determina a velocidade mais provável vmp , que é dada por
(a) vmp = 3kT /m
(b) vmp = 2kT /m
(
)1/2
(c) vmp = 3kT
m
(
)1/2
(d) vmp = 2kT
m
(
)3/2
(e) vmp = 2kT
m
9
19) O trabalho mecânico realizado por um gás ideal numa expansão isotérmica é (V1 = volume
inicial; V2 = volume final)
(a) Igual à quantidade de calor que flui do reservatório para o gás e vale W = NA kT ln(V1 /V2 )
(b) Igual à quantidade de calor que flui do reservatório para o gás e vale W = NA kT ln(V2 /V1 )
(c) Menor do que a quantidade de calor que flui do reservatório para o gás e vale W =
NA kT ln(V2 /V1 )
(d) Menor do que a quantidade de calor que flui do reservatório para o gás e vale
W = NA kT ln(V1 /V2 )
(e) Maior do que a quantidade de calor que flui do reservatório para o gás e vale W =
NA kT ln(V2 /V1 )
20) Quando 1 kg de água a 0 ◦ C é aquecido até 100 ◦ C, sabendo que o calor especı́fico da água
vale 4190 J/kg·K, sua variação da entropia é
(a) 5,31 kJ/K
(b) 5,31 J/K
(c) 1,31 kJ/K
(d) 1,31 m/K
Formulário:
P V = NA kT = nRT
ϵ≡
dQ = dU + pdV
dQ
T
∆Q = mc∆T
dS =
W
T2
=1−
Q1
T1
Q2
T2
=
W
T1 − T2
10
(e) 2,10 mJ/K
Programa de Pós-Graduação
Processo de Seleção − 1o Semestre de 2012
Exame de Conhecimentos em Fı́sica - Gabarito
Questão
Alternativa
1
a b c d e
2
ANULADA
3
a b c d e
4
a b c d e
5
a b c d e
6
a b c d e
7
a b c d e
8
a b c d e
9
a b c d e
10
a b c d e
11
a b c d e
12
a b c d e
13
a b c d e
14
a b c d e
15
a b c d e
16
a b c d e
17
a b c d e
18
a b c d e
19
a b c d e
20
ANULADA