POLÍGONOS CONVEXOS.


POLÍGONOS CONVEXOS
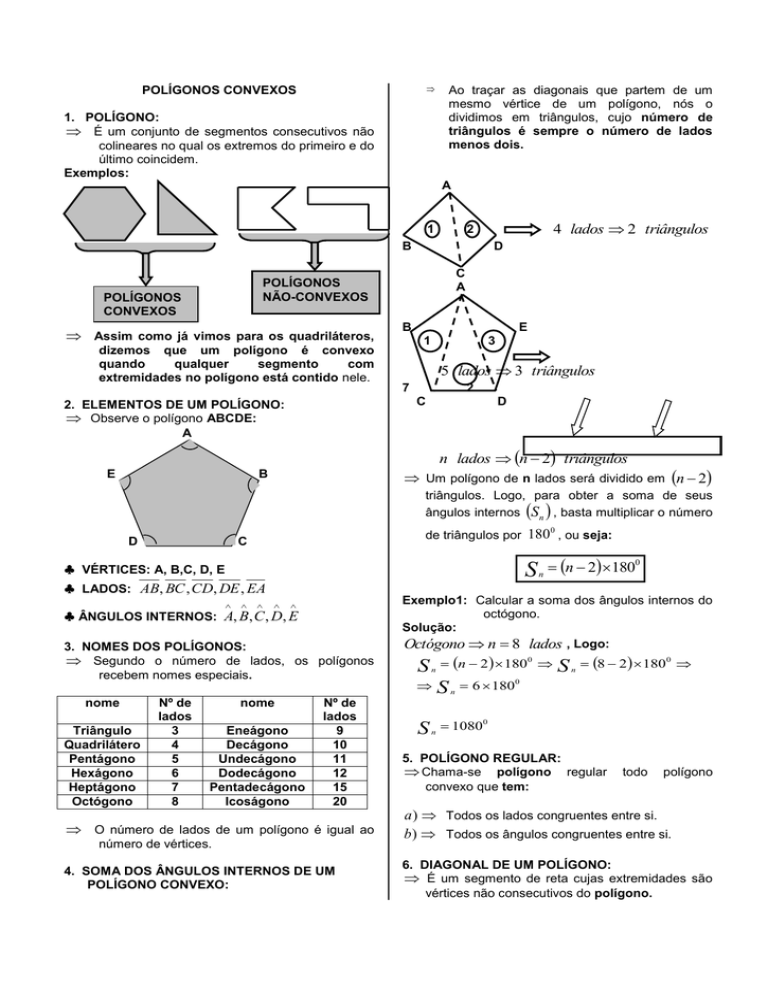
Ao traçar as diagonais que partem de um
mesmo vértice de um polígono, nós o
dividimos em triângulos, cujo número de
triângulos é sempre o número de lados
menos dois.
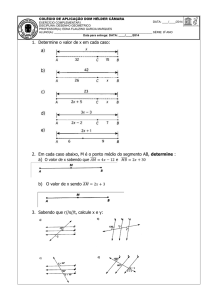
1. POLÍGONO:
 É um conjunto de segmentos consecutivos não
colineares no qual os extremos do primeiro e do
último coincidem.
Exemplos:
A
1
D
C
A
POLÍGONOS
NÃO-CONVEXOS
POLÍGONOS
CONVEXOS
 Assim como já vimos para os quadriláteros,
dizemos que um polígono é convexo
quando
qualquer
segmento
com
extremidades no polígono está contido nele.
B
E
1
3
5 lados  3 triângulos
7
2
C
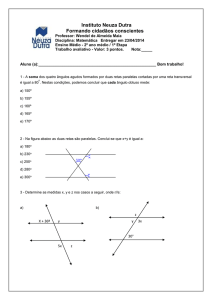
2. ELEMENTOS DE UM POLÍGONO:
 Observe o polígono ABCDE:
A
4 lados  2 triângulos
2
B
D
n lados  n  2 triângulos
E
 Um polígono de n lados será dividido em n  2
B
triângulos. Logo, para obter a soma de seus
ângulos internos Sn , basta multiplicar o número
 
0
D
de triângulos por 180 , ou seja:
C
S  n  2180
0
♣ VÉRTICES: A, B,C, D, E
n
♣ LADOS: AB, BC , CD, DE , EA





♣ ÂNGULOS INTERNOS: A, B, C , D, E
3. NOMES DOS POLÍGONOS:
 Segundo o número de lados, os polígonos
recebem nomes especiais.
nome
Triângulo
Quadrilátero
Pentágono
Hexágono
Heptágono
Octógono
Nº de
lados
3
4
5
6
7
8
nome
Eneágono
Decágono
Undecágono
Dodecágono
Pentadecágono
Icoságono
Nº de
lados
9
10
11
12
15
20
 O número de lados de um polígono é igual ao
número de vértices.
4. SOMA DOS ÂNGULOS INTERNOS DE UM
POLÍGONO CONVEXO:
Exemplo1: Calcular a soma dos ângulos internos do
octógono.
Solução:
Octógono  n  8 lados , Logo:
S
n
 n  2   1800 

S
S
 10800
n
n
S
n
 8  2   1800 
 6  1800
5. POLÍGONO REGULAR:
 Chama-se polígono regular
convexo que tem:
todo
polígono
a )  Todos os lados congruentes entre si.
b )  Todos os ângulos congruentes entre si.
6. DIAGONAL DE UM POLÍGONO:
 É um segmento de reta cujas extremidades são
vértices não consecutivos do polígono.
A
3. (FRANCO) A soma dos ângulos internos de um
0
E
polígono é 1980 . O número de lados do
polígono é:
a) 11
b) 12
c) 13
d) 14
B
Diagonais : AC , AD
D
C
7. NÚMERO DE DIAGONAIS DE UM POLÍGONO:
 Seja um polígono de n lados:
4. (FRANCO) Cada ângulo interno de um decágono
regular mede:
a) 60
0
b) 72
144
0
c) 120
0
d)
0
5. (FRANCO)
O número de diagonais de um
polígono de 14 lados é:
a) 62
b) 68
c) 70
d) 77
6. (FRANCO) Um decágono possui:
a) 42 diagonais
b) 48 diagonais
c) 50 diagonais
d) 54 diagonais
A)  Cada vértice dá origem a n  3 diagonais.
B)  Os n vértices dão origem a n  n  3
diagonais.
C )  Dividimos o resultado por 2 (cada diagonal
foi contada duas vezes).
n  n  3
2
Assim:
d
Onde:
d  número de diagonais

n  número de lados
Exemplo1: Calcule o número de diagonais de um
octógono.
Solução:
 Temos: n  8 octógono
d
n  n  3 8  8  3 8  5 40



 d  20
2
2
2
2
TESTES
1. (FRANCO) Na figura abaixo, quais são polígonos
convexos:
C
a) A e C
b) A e B
A
D
c) B e C
d) B e D
B
2. (FRANCO) A soma dos ângulos internos de um
decágono é:
7. (FRANCO) A soma do número de diagonais com o
número de lados de um decágono é:
a) 35
b) 45
c) 65
d) 80
8.
(FRANCO) O número de diagonais de um
octógono convexo é:
a) 16
b) 18
c) 30
d) n. d. a
9. (FRANCO) De um dos vértices de um polígono
convexo foi possível traçar 9 diagonais. Então, o
polígono tem:
a) 9 lados
b) 10 lados
c) 11 lados
d) 12 lados
10. (FRANCO) O polígono cujo número de diagonais
é igual ao triplo de número de lados é:
a) Pentágono
b) Hexágono
c) Heptágono
d) Eneágono
0
11. (FRANCO) Sendo 1980 a soma das medidas
dos ângulos internos de um polígono convexo,
então este polígono possui:
a) 44 diagonais
b) 65 diagonais
c) 54 diagonais
d) 72 diagonais
12. (FRANCO) Quantos lados tem um polígono cujo
número de diagonais é
a) 6
b) 10 retos
d) 16 retos
c) 10
13. (FRANCO) O valor de x na figura é:
a) 36
b) 72
a) 8 retos
c) 12 retos
b) 8
3
do número de lados?
2
0
1200
0
c) 108
1040
1000
0
d) 104
0
x
x
14. (FRANCO) O valor de x na figura é:
d) 12
0
a) 95
x
b) 100
c) 120
800
0
d) 140
x
0
800
0
x
x
15. (FRANCO) O valor de x na figura é:
a) 80
b) 70
c) 60
0
x
0
0
d) 140
x
x
0
300
G A B A R I T O
1. C
6. D
11. B
2. D
7. B
12. A
3. C
8. D
13. C
4. D
9. D
14. D
5. D
10. D
15. A
300