24/08/2016 logaritmo

Aluno(a) _____________________________________________________________________
INÁCIO ARAÚJO
[email protected]
01 - Determine o valor de:
a) log3 729
b) log2 1024
d) log3264
g) log5
j)
1
125
1
256
1
k) log125
625
h) log64
log 1 125
5
5
m) log3
4
3
i)
log 1 32
2
l) log2
3
o) log2
2
r) log4 2
p) log5 5 5
q) log
s) log0,2 0,04
t) log0,04 0,2
u) log8
v) log9 3
w) log25 0,008
x) log 3 5
27
1
5
27
81
3
4  log5 6
8
k)
e
i) 25
n4
l)
1
 log5 7
2
32log3 2
log 7 log 3
2
m) 2 2
07 – (Mackenzie/SP) Sabendo que x 2  4 x  2log 7 m 2 é um
trinômio quadrado perfeito, determine o logaritmo de m na base
7m.
16
x2
, sabendo que log b x  2 e
3 y
4
5
09 – Se log E = 1 + log a + 2.log b – log c, determine E.
10 – (Unicamp/SP) Calcule o valor da expressão
log n log n
02 – (Vunesp/SP) Considere os seguintes números reais:
a) c < a < b
b) a < b < c
c) c < b < a
1 log2 3
logb y  3 .
93 

y) log1,4  2 

125 

a  1/ 2 , b  log 2 2 e c  log 2
h)
LISTA
3
32 08 – Calcule o valor de log b
3
3
5
LISTA
j) 102+log 3
4
64
n) log16
g)
c) log17 1
f) log2 1
64
n e3
e)
LOGARITMOS
2
. Então:
2
 n
n n
, em que n é um número inteiro,
fazer o cálculo, você verá que esse valor é um número inteiro que
não depende de n.
11 – Usando o fato que log b M 
d) a < c < b
e) b < a < c
n  2 . Ao
log a M
, e sabendo que
log a b
log 2 = 0,30, log 3 = 0,47 e log 7 = 0,84 determine:
a) log128 1024
b) log9 45
c) log2 30
03 - Determinar o valor de x para o qual:
a) logx 128 = 7
d) logx (6-5x) = 2
b) log4 x = 3
e) logx 343 = 3
c) log4 (3x+1) = 2
12 - Considere a função real de variável real, definida por
04 – Sabendo que log 2 = 0,30, log 3 = 0,47 e log 7 = 0,84,
determine:
a) log 4
e) log 15
i) log 2
13– (Unicamp/08) A escala de um aparelho de medir ruídos é
definida como RB = 12 + log10I, em que RB é a medida do ruído,
em bels, e I é a intensidade sonora, em W/m2. No Brasil, a
unidade mais usada para medir ruídos é o decibel, que equivale a
um décimo do bel. O ruído dos motores de um avião a jato
equivale a 160 decibéis, enquanto o tráfego de uma esquina
movimentada de uma grande cidade atinge 80 decibéis, que é o
limite a partir do qual o ruído passa a ser nocivo ao ouvido
humano.
a) Escreva um fórmula que relacione a medida do ruído R dB, em
decibéis, com a intensidade sonora I, em W/m2. Empregue essa
fórmula para determinar a intensidade sonora máxima que o
ouvido humano suporta sem sofrer qualquer dano.
b) log 5
c) log 6
d) log 14
f) log 50
g) log 150
h) log 0,125
j) log
05 – (U.F. Juiz de Fora) Considere a função f: IR
f(x) = 3 + 2–x. Então f( log 2 5 ) é igual a:
a) 4/5
3
 IR definida
por f(x) = log10 ( x 2  6 x  10) . Então o valor de f(6) - f(-2) é:
a) 26
b)
log10 26
d) log10
c) 1
5
13
e) 1+
log10 26
b) 8/5
c) 12/5
d) 16/5
e) 4
a)
3log3 2
b)
4 log2 3
c)
16 log2 5
b) Usando a fórmula dada no enunciado ou aquela que você
obteve no item (a), calcule a razão entre as intensidades sonoras
do motor de um avião a jato e do tráfego em uma esquina
movimentada de uma grande cidade.
d)
81log3 6
e)
125log5 13
f)
3 2 log3 2
14 – (UFCE) Sendo a e b números reais positivos tais que
06 – Determine o que se pede:
log
3
a = 224 e log 3 b = 218, calcule o valor de a/b.
x
15 – (UEL PR) Seja a equação exponencial: 9
 1 
  .
 27 
x 3
Assinale a alternativa que contém a solução da equação
exponencial dada.
a) x = -6
b) x = 
6
5
c) x =
5
6
d) x =
h) 223; i) 245; j) 300;k) 4; l) 4; m) 21; 07 – 1/2; 08 – { - 5}; 09 –
E=
10ab2
c
; 10 – {n = -2}; 11 – a) 10/7; b) 82/47; c) 4,9 ; 12 – d; 13 – a) RdB
= 120 + 10.log10I; 10-4W/m2;
b) 108; 14 – 27; 15 – b; 16 – b; 17 –d; 18 – d; 19 – b; 20 – b; 21 – a; 22 – e;
5
2
01 – Determine o valor de
16 – (UCS RS) Ao estudar o processo de reprodução em uma
cultura de bactérias, um grupo de biólogos, a partir de dados
experimentais coletados em um determinado período de tempo,
concluiu que o número aproximado de indivíduos,
tempo t em horas, é dado por N(t) = 50x2 0,3t . Dessa forma, a
cultura terá 3 200 indivíduos depois de:
a) 12 horas
b) 20 horas
c) 15 horas
d) 23 horas
log3 5  log 7 70 sabendo que
log3 45  3,464974 e log7 10  1,1833 .
02 – Calcule:
a)
 log6 5. log5 6
b)
log5 1  4log4 5  log3  log5 (125) 
c) 49
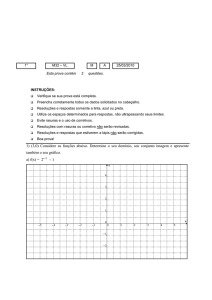
17 - (UFRRJ) O gráfico abaixo descreve a função f(x) = a2x – 1, em d)
que é positivo. Nessas condições qual o valor de a?
e)
log7 2
 25log5 3
2 log2 7log2 3
2 22 log2 5
03 – Determine o valor dos logaritmos abaixo sabendo que
log 2  0,301 , log 3  0, 477 e log 7  0,845 .
a)
log3 7
b)
log7 21
c)
log9 16
04 – (PUC/RS) O conjunto solução da equação
18 – (UEPI) Se
9
p1
3
2
log x 10  3x   2 , em IR, é:
a) 
b) {-2}
c) {5}
1
e log 2  q  1  , então
2
a) 4
x
2
b) 5
c) 6
d)7
e) 8
19 – (UECE) Se x1 e x2 são as raízes da equação x + 6x + 4 = 0,
então log4 (5x1x2 – 2x1 – 2x2) é igual a:
a) 3/2
b) 5/2
c) 3
d) 5
20 – (UFCE) A opção em que figuram as soluções da equação
a) -3 e -2
b) -3 e 3

   0 é:

c) -2 e 3
0,30103
0, 69897
0, 69897
b)
0,30103
c) 0,30103
é igual a:
x
a)
3
2x
b)
3
log 4 25 
e) log10
 log9 2 . log2 5.log5 3 é igual
06 – (FGV/SP) O produto
d) -2 e 2
e) 2 e 3
a:
a) 0
21 – (UFMT) Sendo
d) 0, 69897
a)
2
2


3x 8  log10 log10  10 10 10 10


b)
1
2
c) 10
d) 30
x
, podemos afirmar que log 2 5
3
07 – A expressão log 2 3.log 3 5.log 5 10 
x2
c)
9
d)
3
x
3
e)
3
e){-5, 2}
05 – O valor de x equação 2  5 , sabendo que
log 2  0,30103 e log 5  0, 69897 é:
p  p.q  q é igual a:
2
d) {-2; 5
x2
9
22 – Supondo que exista, o logaritmo de a na base b é:
a) a potência de base b e expoente a.
b) a potência de base a e expoente b.
c) o número ao qual se eleva a para se obter b.
d) a potência de base 10 e expoente a.
e) o número ao qual se eleva b para se obter a.
Gabarito
01 – a)6; b)10; c)0; d)7/5; e) 3; f) - 5; g) -3; h) -8/5; i)-5/2; j) -3; k) -4/3; l) 1/2; m)
1/5; n) 3/8; o) 5/3; p) 3/2; q) -20/9; r) -1/3; s) 2; t) ½; u) 4/9; v) 5/4; w) -3/2; x) ¾;
y) 3; 02 – a; 03 – a) 2; b) 64; c) 5; d) {-6, 1}; e) 7; 04 – a) 0,60; b) 0,70; c) 0,77;
d) 1,14;
e) 1,17; f) 1,70; g) 2,17; h) – 0,90; i) 0,15; j) 0,235;
05 – d; 06 – a) 2; b) 9; c) 625; d) 1296; e) 2197; f) 18; g) 625/6;
e)
1
10
1
é equivalente
log 5 4
a:
a)
log 2 50
d)
log 2 2 2
b)
log2 10 5
e)
log 2 2
c)
log2 5 10
08 – Considerando log 2  0,3010 e log 3  0, 4771 calcule:
a)
log 6 4
b) log
6
c) log 3 12
d) co log 72
Gabarito
01 – 3,648274; 02 – a) 1; 6; c) -5; d) 21; e) 100; 03 – a) 1,771; b) 1,564; c) 1,262;
04 – c; 05 – b; 06 – b; 07 – b; 08 – a) 0,7736; b) 0,38905; c) 0,3597; d) -1,8572;