Oficina 8: Sistema de Part´ıculas

Universidade Federal do Rio de Janeiro — Instituto de Fı́sica
Apoio Pedagógico das Turmas de 6 horas — 2017/1
Oficina 8: Sistema de Partı́culas
8 de Maio de 2017
ATENÇÃO: As questões só serão aceitas mediante desenvolvimento e
justificativas plausı́veis!
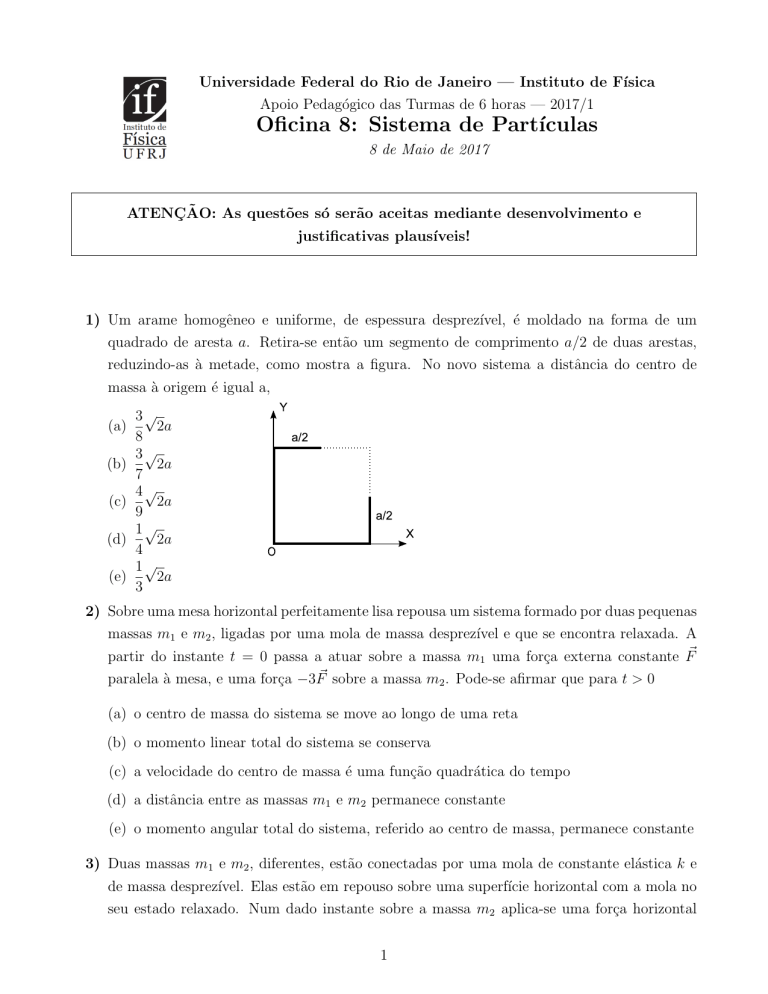
1) Um arame homogêneo e uniforme, de espessura desprezı́vel, é moldado na forma de um
quadrado de aresta a. Retira-se então um segmento de comprimento a/2 de duas arestas,
reduzindo-as à metade, como mostra a figura. No novo sistema a distância do centro de
massa à origem é igual a,
(a)
(b)
(c)
(d)
(e)
3√
2a
8
3√
2a
7
4√
2a
9
1√
2a
4
1√
2a
3
2) Sobre uma mesa horizontal perfeitamente lisa repousa um sistema formado por duas pequenas
massas m1 e m2 , ligadas por uma mola de massa desprezı́vel e que se encontra relaxada. A
partir do instante t = 0 passa a atuar sobre a massa m1 uma força externa constante F~
paralela à mesa, e uma força −3F~ sobre a massa m2 . Pode-se afirmar que para t > 0
(a) o centro de massa do sistema se move ao longo de uma reta
(b) o momento linear total do sistema se conserva
(c) a velocidade do centro de massa é uma função quadrática do tempo
(d) a distância entre as massas m1 e m2 permanece constante
(e) o momento angular total do sistema, referido ao centro de massa, permanece constante
3) Duas massas m1 e m2 , diferentes, estão conectadas por uma mola de constante elástica k e
de massa desprezı́vel. Elas estão em repouso sobre uma superfı́cie horizontal com a mola no
seu estado relaxado. Num dado instante sobre a massa m2 aplica-se uma força horizontal
1
F~ de módulo constante, cuja direção passa pelos centros das massas; como mostra a figura.
Para a aceleração do centro de massa das massas, a opção correspondente a esta situação é:
(a) ~aCM = F~ /(m1 + m2 )
(b) ~aCM = F~ /m1 − F~ /m2
(c) ~aCM = F~ /m2
(d) ~aCM = F~ /m1 + F~ /m2
(e) nenhuma das respostas
anteriores
4) Dois discos de massas m e 3m estão ligados por uma mola ideal comprimida sobre uma mesa
horizontal lisa. Em um dado instante a força da mola sobre o primeiro disco é F~el e uma
força F~ paralela ao plano da mesa está aplicada sobre o segundo disco, como mostra a figura
(mesa vista de cima). No instante considerado a aceleração do centro de massa do sistema
constituı́do pelos discos e pela mola é
F~
;
(a)
4m
(b)
F~ + F~el
;
4m
(c)
F~ + 2F~el
;
4m
(d)
F~ − 2F~el
;
4m
(e)
F~ − F~el
.
4m
5) Um sapo está, inicialmente, situado num dos extremos de uma plataforma de comprimento
l que flutua, em repouso, sobre as águas paradas de um lago. Num dado instante, o sapo dá
um salto com uma velocidade de módulo v0 e que faz com a horizontal um ângulo θ como
mostra a figura. Suponha que a plataforma se movimente apenas na horizontal e despreze
o atrito entre a água e a plataforma. Seja m a massa do sapo e M a massa da plataforma.
Após o sapo pular, pode-se afirmar que:
(a) a plataforma se move para esquerda com velocidade de módulo
2
m
v cosθ
M 0
(b) a plataforma se move para esquerda com velocidade de módulo
m
v
M 0
(c) a plataforma se move para direita com velocidade de módulo v0
(d) a plataforma se move para esquerda com velocidade de módulo v0
(e) a plataforma se move para esquerda com velocidade de módulo
m
v senθ
M 0
(f) a plataforma não se move
6) Uma bola desloca-se com velocidade ~v constante e colide elasticamente na lateral de uma
mesa, segundo o ângulo α definido entre a direção de seu movimento e a lateral da mesa e
é claro que |~v | = |~v 0 |; como mostra a figura. O processo de colisão dura um tempo ∆t. Na
figura estão indicadas 4 setas numeradas. A opção correta para representar a força média
que atua na bola durante a colisão é:
(a) nenhuma das respostas anteriores.
(b) 1.
(c) 2.
(d) 3.
(e) 4.
7) Duas bolas A e B idênticas são liberadas da mesma altura h e caem verticalmente sobre uma
superfı́cie horizontal. A bola A colide elasticamente com a superfı́cie enquanto a bola B ao
colidir permanece na superfı́cie. A duração do tempo de colisão de ambas as bolas com a
superfı́cie é o mesmo e FA e FB são as intensidades das forças médias que atuaram sobre as
bolas A e B respectivamente. Podemos afirmar que
(a) FA = 2FB ;
(b) FA = FB ;
(c) FA < FB ;
(d) FA 6= 0 e FB =0;
(e) FA = FB /2.
3
8) Um bloco de massa m e velocidade ~v colide com outro bloco de massa 2m e velocidade
−~v . Após a colisão eles ficam unidos. Se P~ é o momento linear total dos blocos e V~CM é a
velocidade do centro de massa do sistema formado pelos dois blocos, a opção correta é
(a) V~CM = −~v /3, antes e após a colisão
(b) O momento linear P~ não é conservado pois a colisão é inelástica
(c) |V~CM | = 0 antes da colisão
(d) |V~CM | = 0 depois da colisão
(e) P~ = 3m~v
(f) P~ = mV~CM
9) O gráfico abaixo mostra o comportamento com o tempo da força F (t) que um taco realiza
sobre uma bola de golfe de massa m, que está inicialmente em repouso quando atingida pelo
taco. O força chega a um valor máximo F0 em t = 3t0 . Das afirmações que se seguem,
assinale aquela que é INCORRETA.
F (t )
F0
0
5t0
t0
t
(a) O módulo do impulso produzido pelo taco é dado por J = 4F0 t0
(b) A aceleração média da bola será amed = 0, 5F0 /m
(c) A velocidade da bola após a tacada será v = 2F0 t0 /m
(d) A variação do momento linear da bola é fornecida pela área sombreada no gráfico
(e) A aceleração máxima da bola é amax = F0 /m
4
10) Uma astronauta com sua caixa de ferramentas encontra-se no espaço sideral próxima à sua
nave, todos muito afastados do restante do universo e com velocidades nulas relativamente a
um referencial inercial. Em um dado instante a astronauta arremessa sua caixa de ferramentas com velocidade de módulo v, conforme indica a figura; com isso a astronauta percorre
uma distância D até chegar à nave. Sabendo-se que a massa da astronauta é M e a da caixa
de ferramentas é m, conlcuı́mos que o tempo que a astronauta leva para percorrer a distância
D é
(a) DM/mv.
(b) Dm/M v;
(c) D/v;
(d) DM/[(m + M )v];
(e) Dm/[(M + m)v];
5