LISTA 27 Curva de Energia Potencial

Universidade Tecnológica Federal do Paraná - UTFPR
Disciplina de Física I
Prof. Nelson Elias
27ª Lista de Exercícios: Cap.8 Curva de Energia Potencial - EXERCÍCIOS ADICIONAIS
Aluno: ___________________________ Turma: _______ Data: ______/_____/________.
1) Uma força paralela ao eixo Ox atua sobre uma partícula que desloca ao longo deste eixo. Essa força produz uma
energia potencial dada por U(x) = αx4, onde α = 1,20 J/m4.
Qual é o módulo da força quando a partícula se encontra em x = - 0,80m?
Da Eq. (8-20) da pág 143 6ª ed.
Fx = −
dU
= − 4αx 3 = − ( 4.8 J / m 4 ) x 3 , e portanto
dx
Fx (−0.800 m) = − (4.8 J / m 4 )(− 0.80 m ) = 2.46 N .
3
2) Uma única força conservativa F = (6,0 x – 12)i N, onde x está em metros, atua sobre uma partícula que se move ao
longo de um eixo x. A energia associada com esta força tem valor 27 J em x = 0. a) Escreva uma expressão para a
energia potencial U(x) como função da posição x. b) Qual é o máximo valor positivo da energia potencial? Para qual
valor negativo e positivo de x a energia potencial é nula?
a)
b)
x em x = 2 m U(2m) = 39 J
c) x = -1.6 m e x = 5,6 m.
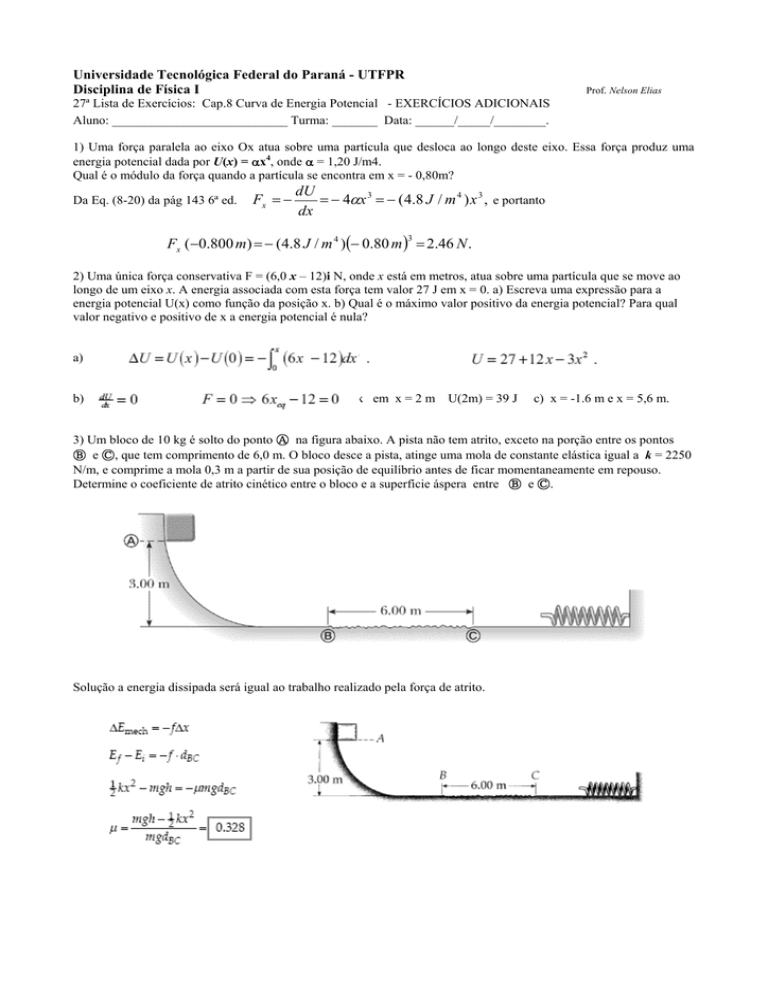
3) Um bloco de 10 kg é solto do ponto Ⓐ na figura abaixo. A pista não tem atrito, exceto na porção entre os pontos
Ⓑ e Ⓒ, que tem comprimento de 6,0 m. O bloco desce a pista, atinge uma mola de constante elástica igual a k = 2250
N/m, e comprime a mola 0,3 m a partir de sua posição de equilíbrio antes de ficar momentaneamente em repouso.
Determine o coeficiente de atrito cinético entre o bloco e a superfície áspera entre Ⓑ e Ⓒ.
Solução a energia dissipada será igual ao trabalho realizado pela força de atrito.
4) Um bloco de massa m = 2 ,0 kg é solto de uma altura h = 40 cm sobre uma mola de constante elástica k = 1960 N/m
(conforme a figura). Determine o comprimento máximo que a mola é comprimida.
5) Uma bola de massa 0,50 kg é arremessada de P como mostrado na figura abaixo. A bola tem velocidade inicial vi
com uma componente horizontal de 30,0 m/s. A bola sobe até uma altura de 20,0 m acima de P. Utilizando a lei de
conservação da energia, determine (a) a componente vertical da velocidade inicial; (b) o trabalho feito pela força
gravitacional sobre a bola durante seu movimento de P até B; e (c) as componentes horizontal e vertical do vetor
velocidade quando a bola alcança B.
Inicialmente por conveniência colocamos nosso
referencial em P assim a bola possuirá apenas energia
cinética. No ponto mais alto da trajetória bola terá a
mesma energia mecânica inicial na forma de cinética e
potencial gravitacional, dessa forma poderemos
calcular a componente viy da velocidade inicial.
Desde que a componente vy da velocidade inicial é mesma no nível do ponto P. Teremos que calcular apenas o trabalho
da força gravitacional nos últimos 60 m.
c) No ponto B a velocidade vy poderá ser obtida por: