Equação de movimento para um foguete - IFSC-USP

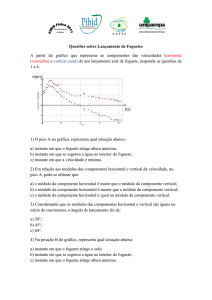
Equação de movimento para um foguete
Considere um foguete de massa instantânea m. Com relação a um observador inercial, seja v a velocidade do foguete. Parte da massa m do foguete é constituída
pelo combustível que é expelido para fora através de um motor. Seja
γ
−
=
dm
dt
(1)
a taxa a que a massa do combustível é expelida para fora do corpo do foguete.
Veja que γ é uma quantidade positiva, já que o foguete perde massa e, portanto,
dm/dt < 0. Se a velocidade de ejeção do combustível, com relação ao foguete,
é dada por ve , então a velocidade do combustível, com relação ao observador
inercial mencionado acima é dada por
vcomb
=
ve + v.
(2)
Vamos utilizar a conservação do momentum para deduzir a equação de movimento do foguete. Para isso, vamos supor que não haja nenhuma força externa
agindo sobre o sistema composto pelo foguete e seu combustível. Em um determinado instante de tempo, t, o momentum do foguete é dado por
pf og (t)
= mv.
(3)
Vamos definir o sistema como sendo o foguete e o combustível em seu interior
no instante t. Sendo assim, nesse instante o momentum total do sistema é dado
pela Eq. (3). Depois de um intervalo de tempo dt, o momentum do foguete é
dado por
pf og (t + dt)
=
(m − |dm|) (v + dv) ,
(4)
já que uma quantidade de massa de combustível de módulo |dm| é lançada
pelo motor para fora do foguete. O momentum total no instante t + dt não é
apenas o momentum do foguete, mas há também o momentum da massa |dm|
de combustível que adquire a velocidade vcomb ao ser expelida para fora. Então,
o momentum total no instante t + dt é dado por
ptot (t + dt)
=
pf og (t + dt) + |dm| vcomb .
(5)
Na ausência de forças externas, o momentum total deve ser conservado durante
o intervalo de tempo dt e, portanto, igualando as Eqs. (3) e (5), obtemos
mv
= pf og (t + dt) + |dm| vcomb .
Da Eq. (4) segue
mv
=
(m − |dm|) (v + dv) + |dm| vcomb ,
mv
=
mv − v |dm| + mdv + |dm| vcomb ,
isto é,
1
onde desprezamos termos infinitesimais de segunda ordem. Simplificando, obtemos
(vcomb − v) |dm| + mdv
= 0.
Usando a Eq. (2), vem
ve |dm| + mdv
= 0.
Dividindo essa equação por dt resulta em
|dm|
dv
+m
= 0.
dt
dt
Como a massa do foguete decresce com o tempo, segue que
ve
|dm|
dt
= −
dm
dt
e, assim,
dv
=
dt
Usando a Eq. (1), podemos escrever
m
ve
dm
.
dt
dv
= −γve .
dt
A taxa de variação do momentum do foguete é dada por
m
d (mv)
dv
dm
dpf og
=
=m
+v
= −γ (ve + v) ,
dt
dt
dt
dt
usando a Eq. (1). Assim, a força total resultante sobre o foguete, de acordo
com a segunda lei de Newton, é dada por −γ (ve + v) . Essa é a força obtida
pela expulsão de combustível. Se, além dessa força, houver outra força externa
resultante, F, sobre o foguete, como a força peso, por exemplo, então a segunda
lei de Newton fornece
dpf og
= −γ (ve + v) + F
dt
e, portanto, como
dpf og
dv
dm
= m
+v
,
dt
dt
dt
segue que
dv
dm
m
+v
= −γ (ve + v) + F,
dt
dt
isto é,
dv
m
− γv = −γ (ve + v) + F,
dt
ou seja,
dv
m
= −γve + F,
dt
que é a equação de movimento para o foguete sob a ação de uma força externa.
2
References
[1] Keith R. Symon, Mechanics, terceira edição (Addison Wesley,
1971).
3