5. Tópicos: Problemas em grafos. Algoritmo de Dijkstra para

5. Tópicos: Problemas em grafos. Algoritmo de Dijkstra para determinação de
caminhos mı́nimos. Determinação de caminhos de capacidade máxima em redes
de fluxo por adaptação do algoritmo de Dijkstra. (* Pergunta de valorização *)
Resposta:
O algoritmo que se descreverá combina o algoritmo de determinação de caminhos de capacidade máxima com o de determinação de caminhos de comprimento mı́nimo (dados na
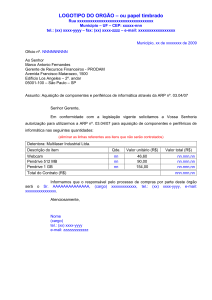
disciplina). Começa-se por ilustrar a sua ideia, usando a rede dada na figura.
B
p
p
p
(5,6) p
p
p
pp
ppp
(3,7)
(0, ∞, −)
NNN
NN(1,2)
NNN
NNN
(4,3)
C
A (∞, 0, −)
NNN
p
NNN
(5,4) ppp
p
NNN
p
p
p
NN
(2,10)
ppp
D (0, ∞, −)
E
(1,5)
H
(0, ∞, −)
NNN
NN(6,7)
NNN
NNN
(14,9)
(7,6)
F (0, ∞, −)
G
ggg
g
g
g
ggggg
ggggg(8,7)
g
g
g
gg
(2,3)
(0, ∞, −)
(4,5)
(0, ∞, −)
(0, ∞, −)
O terno que se coloca inicialmente em cada nó é da forma (c, t, p), onde c designa a capacidade
do caminho, t a sua duração, e p o nó antecedente no caminho (para que este possa ser
reconstruı́do por análise para trás). A inicialização destes valores é semelhante à efectuada
nos algoritmos referidos. Note-se que em v0 = A se tem um terno diferente dos restantes,
concretamente (∞, 0, −). Supõe-se que ∞ é maior do que qualquer número real. Será usado ∗
para assinalar ternos definitivos. Inicialmente todos os ternos são provisórios.
Em cada iteração será escolhido um dos “melhores” ternos provisórios. No contexto do
problema proposto, “melhor” quer dizer “dentre os que têm maior capacidade, é aquele
que tem menor duração”. É de salientar que esta escolha é fundamental para garantir a
correcção do algoritmo. Marca-se esse terno escolhido como definitivo e actualizam-se os
ternos provisórios dos nós adjacentes.
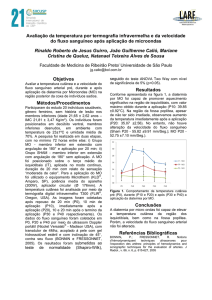
Na primeira iteração, é marcado o terno (∞, 0, −) em A e substituı́dos os ternos provisórios
de B, C e D, passando a ter:
B
o
o
o
(5,6) o
o
o
oo
ooo
(3,7)
(5, 6, A)
NNN
NN(1,2)
NNN
NNN
(4,3)
C
A ∗(∞, 0, −)
OOO
p
OOO
(5,4) ppp
p
OOO
p
p
p
OO
(2,10)
ppp
D (2, 10, A)
E
(1,5)
H
(0, ∞, −)
NNN
NN(6,7)
NNN
NNN
(14,9)
(7,6)
F (0, ∞, −)
G
ggg
g
g
g
g
gggg
gggg(8,7)
g
g
g
g
gg
(2,3)
(4, 3, A)
(4,5)
(0, ∞, −)
(0, ∞, −)
Na segunda iteração, marca-se o terno (5, 6, A) de B como definitivo. Actualiza-se o terno
de H. Não se actualiza o de C pois (min(5, 1), 6 + 2, B) = (1, 8, B) é pior do que (4, 3, A).
Também não se alteraria o terno de A, não só por já ser definitivo mas também porque, A é o
nó que antecede B no caminho óptimo que corresponde ao terno (5, 6, A), e é conhecido que
nenhum caminho com ciclos tem comprimento mı́nimo. Nesta segunda iteração obtem-se:
B
o
o
o
(5,6) o
o
o
oo
ooo
(3,7)
∗(5, 6, A)
NNN
NN(1,2)
NNN
NNN
(4,3)
A ∗(∞, 0, −)
C
OOO
p
OOO
(5,4) ppp
p
OOO
p
pp
OO
(2,10)
ppp
D (2, 10, A)
E
(1,5)
H
(3, 13, B)
NNN
NN(6,7)
NNN
NNN
(14,9)
(7,6)
F (0, ∞, −)
G
ggg
g
g
g
g
gggg
gggg(8,7)
g
g
g
g
gg
(2,3)
(4, 3, A)
(4,5)
(0, ∞, −)
(0, ∞, −)
Na terceira iteração, seria escolhido o terno (4, 3, A) de C e obtem-se:
B
p
(5,6) ppp
p
p
p
p
ppp
(3,7)
∗(5, 6, A)
(1, 5, C)
NNN
NN(1,2)
NNN
NNN
(4,3)
A ∗(∞, 0, −)
C
OOO
p
OOO
(5,4) ppp
p
OOO
p
p
p
OO
(2,10)
ppp
D (4, 7, C)
E
(1,5)
∗(4, 3, A)
(4,5)
H
(3, 13, B)
NNN
NNN(6,7)
NNN
(2,3)
NN
(14,9)
(7,6)
F (4, 12, C)
G
ggg
g
g
g
g
gggg
ggggg(8,7)
g
g
g
g
gg
(0, ∞, −)
(4, 8, C)
O terno (1, 5, C) é acrescentado em B porque não é pior do que (5, 6, A), para encomendas
até 1Kg. O terno (4, 7, C) substitui (2, 10, A) em D porque este último era pior.
Na quarta iteração, marcaria o terno (4, 7, C) em D como definitivo. . . e prosseguiria. O
algoritmo terminará quando não existirem mais ternos provisórios.
Formalmente, para G = (V, E, δ) nas condições do enunciado, δ(e) = (δ1 (e), δ2 (e)) designando a capacidade e duração do ramo e, para todo e ∈ E, se “(c, t, p) : v” representar o terno
provisório escolhido numa dada iteração e o nó a que pertence, a actualização consiste em:
Para cada w ∈ Adjs(v) \ {p}, verificar se existe algum terno definitivo (c′ , t′ , p′ )
em w tal que (min(c, δ1 (vw)), t + δ2 (vw)) não seja melhor do que (c′ , t′ ), isto é, tal
que min(c, δ1 (vw)) ≤ c′ e t+δ2 (vw) ≥ t′ . Se existir, não alterar nada em w. Senão,
retirar todos os ternos provisórios (c′ , t′ , p′ ) de w tais que c′ ≤ min(c, δ1 (vw)) e
t′ ≥ t + δ2 (vw) e colocar o terno (min(c, δ1 (vw)), t + δ2 (vw), v) em w.
Em resumo, o algoritmo seria:
Pv0 ← (∞, 0, −)
Q ← (∞, 0, −) : v0
Para todo v ∈ V \ {v0 } fazer
Q ← inserir (0, ∞, −) : v em Q, mantendo-a ordenada.
Enquanto Q for não vazia, fazer
Retirar o primeiro elemento de Q; seja (c, t, p) : v esse elemento
Marcar (c, t, p) como terno definitivo
Para cada w ∈ Adjs(v) \ {p} fazer
cw ← min(c, δ1 (vw))
tw ← t + δ2 (vw)
Se não existir terno definitivo (c′ , t′ , p′ ) em Pw com cw ≤ c′ e tw ≥ t′
retirar de Pw os ternos provisórios (c′ , t′ , p′ ) tais que cw ≥ c′ e tw ≤ t′ , e
retirar de Q os elementos (c′ , t′ , p′ ) : w correspondentes
Pw ← inserir (cw, tw, v) em Pw
Q ← inserir (cw, tw, v) : w em Q, mantendo-a ordenada.
No algoritmo, Q representa uma fila de prioridades: à cabeça terá sempre o terno provisório
melhor (ou um dos melhores). No fim, qualquer que seja v ∈ V , a tabela/lista Pv conterá
ternos definitivos: cada terno (c, t, p) identifica um caminho óptimo para as encomendas
até c Kg (inclusivé) que a enviar de v0 para v. Por análise para trás, reconstroi-se o caminho
se necessário (p é o nó que antecede v nesse caminho).
Em cada fase do algoritmo, os ternos definitivos já propagaram toda a informação relevante.
Os ternos provisórios são os que ainda vão poder efectuar alterações. A correcção do algoritmo resulta de, em cada iteração, se escolher o melhor terno provisório. Não é possı́vel
melhorar esse terno pois os restantes provisórios são piores do que esse ou igualmente bons.
(FIM)