Cap. 20

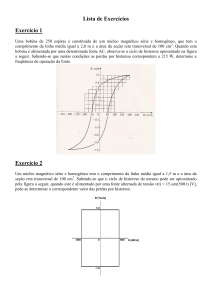
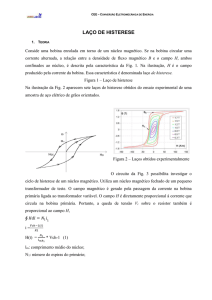
ELETROMAGNETISMO II
20
187
COMPORTAMENTO EM C. A. DOS
MATERIAIS FERROMAGNÉTICOS
Este capítulo é dedicado a fenômenos que ocorrem em materiais ferromagnéticos, quando estes são
submetidos a campos magnéticos variáveis no tempo. Estes fenômenos ocorrem porque os
materiais ferromagnéticos além de serem bons condutores para o fluxo magnético, também se
enquadram na categoria dos materiais condutores de corrente elétrica (não tão bons condutores
como o cobre, o alumínio e o ouro, por exemplo)
20.1 - Permeabilidade Diferencial e Permeabilidade Incremental
Como vimos no capítulo passado, o cálculo de indutâncias requer o conhecimento de
permeabilidades magnéticas que não são constantes, variando na medida em que a intensidade de
campo magnético ao qual o material ferromagnético está submetido também varia. Esta
permeabilidade, por sua vez, varia com as correntes nos enrolamentos, responsáveis pela excitação
dos campos magnéticos. Entretanto, para certas aplicações, devemos definir um número que
expresse esta permeabilidade magnética. Portanto, algumas considerações devem ser feitas aqui.
A indutância definida como a relação entre o fluxo concatenado e a corrente, só é válida quando  é
constante. No caso dos materiais ferromagnéticos,  não é constante e escrevemos para a
indutância:
L
d
d
N m
di
di
(20.1)
Para o circuito magnético da figura 20.1 de comprimento médio  , podemos escrever que:
m  S B  dm  S dB
(20.2)
Da mesma forma
N i H  di  
dH
N

I
N
Figura 20.1 - Estrutura ferromagnética com um enrolamento
Portanto, de (20.1) temos:
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
(20.3)
188
ELETROMAGNETISMO II
L
N2S dB
 dH
(20.4)
O fator dB/dH com dimensão de permeabilidade magnética corresponde à declividade (variável) na
curva de histerese. Conforme podemos observar na figura 20.2, a relação dB/dH, por sua razão de
ser, é conhecida por permeabilidade diferencial, maior do que a relação Bi/Hi no mesmo ponto i.
B (T)
Bi
dB/dH
Hi
H (A/m)
Figura 20.2 - Ciclo de Histerese com representação de B, H e dB/dH.
Se uma corrente alternada é aplicada ao circuito, tal que dB/dH varie de instante a instante, fica
impraticável utilizarmos o conceito de indutância. Neste caso, é conveniente utilizar uma indutância
média Lav, definida como:
L av 
onde  
N2S  dB 
N2S

 
  dH  av

(20.5)
B max
H max
Bmax
Figura 20.3 – representação da
permeabilidade magnética média
como sendo a relação Bmax/Hmax
Hmax
Suponhamos agora que em adição a uma pequena corrente alternada, tenhamos uma componente
DC (corrente contínua) relativamente grande. Neste caso, pequenos laços de histerese existirão em
cada ponto do ciclo de histerese principal, como pode ser visto na figura 20.4.
Neste caso, o valor médio dB / dH é dado por B / H onde B e H são as diferenças entre os
extremos do laço de histerese menor onde B / H recebe o nome de permeabilidade incremental.
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
189
ELETROMAGNETISMO II
B
H
Figura 20.4 - Laço de histerese com laços de histereses secundários
20.2 - Correntes Parasitas
Quando uma massa metálica ferromagnética é submetida a uma densidade de fluxo com indução
variável no tempo, forças eletromotrizes serão induzidas no seu interior, produzindo laços ou espiras
de correntes parasitas que circularão pelo metal. Tais correntes parasitas são também conhecidas
por correntes de Foucault, que encontrando resistência, aquecem o material dissipando energia.
Considere a figura 20.5, onde uma chapa ou lâmina de material ferromagnético, de espessura ,
comprimento um pouco maior do que  e profundidade a, é submetida a um campo magnético
variável, no tempo, na direção do eixo x, ou seja, perpendicular a área   (plano do papel) dele
saindo.

z
i
B
y

i
Figura 20.5 - Chapa de material magnético submetida a campo variável
A análise que faremos se restringe a chapas ou lâminas de material ferromagnético, onde  >>, na
presença de campos magnéticos de indução senoidal, uniformemente distribuído ao longo da seção
transversal   de modo que:

B  B0 cos t  â x
(20.6)
A presença deste campo magnético de indução senoidal no tempo induz laços de corrente alternada
no meio ferromagnético, ocorrendo por conseqüência a dissipação de energia. Considerando o
material como uma chapa ou lâmina de espessura <<  , podemos admitir que os laços de corrente
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
ELETROMAGNETISMO II
190
parasita praticamente acompanham o perfil da lâmina e assim considerar apenas as diferenças de
potencial na direção y em decorrência da fem e induzida segundo a lei de Faraday, conforme
e
d
dt

s
 
B  dS
(20.7)
Para um laço genérico de corrente induzida na chapa, podemos escrever que
e  2 z  B0 sen t .
(20.8)
Como já vimos em capítulos anteriores a fem induzida encontra-se na espira e estabelece a
circulação da corrente induzida em cada laço. Assim, cada laço de corrente induzida percorrendo a
chapa, pela lei de Joule, dissipará uma potência dada por:
dP 
E 2ef
dR
(20.9)
onde R é a resistência do percurso significativo 2  com resistividade específica  percorrido por cada
laço de corrente induzida. Assim,
dR  
2
a dz
(20.10)
Portanto, a potência média dissipada na lâmina em cada laço de corrente será:
2 z   B0 2
dP
2

2
adz

2  B02 a z 2 dz

(20.11)
A potência total dissipada na lâmina será dada pela integração da potência em cada laço de
corrente, para z variando de 0 a /2. Desta forma, a potência dissipada em toda a espessura  da
chapa pela circulação das correntes parasitas envolventes ou de Foucault será então:
/ 2
Pf 

0
B02 2  a z 2 dz

(20.12)
O caminho oferecido pelos laços de correntes parasitas encontra uma resistência elétrica no percurso
fechado 2  . Daí considerarmos apenas a metade da espessura da chapa no cálculo da potência
dissipada na lâmina para que não a tomemos duas vezes, valor este já considerado na equação
(20.10) na determinação da resistência elementar dR em cada laço de corrente. Assim,
Pf 
B20 2  a 3
24 
(20.13)
Sendo o volume da lâmina  a , as perdas por unidade de volume no Sistema Internacional de
Unidades será:
p fv 
B 20 2  a 3 B02 2  2  W 



24   a 
24   m3 
ou:ainda
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
(20.14)
191
ELETROMAGNETISMO II
p fv 
B 02 2  2 
24
W 


 m3 
(20.15)
Vemos então que as perdas por correntes parasitas são:
1.
2.
3.
4.
proporcionais ao quadrado da indução magnética B;.
proporcionais ao quadrado da freqüência f ou , onde  = 2f;
proporcionais ao quadrado da espessura da chapa do material magnético;
proporcionais à condutividade (ou inversamente proporcionais à resistividade).
20.3 - Perdas por Histerese
O material ferromagnético quando submetido a um campo magnético variável no tempo se aquece
por duas razões; uma delas, já vista, pela indução de correntes parasitas ou de Foucault e outra por
dissipação de energia na inversão dos dipolos ou domínios magnéticos existentes no meio, que são
as perdas por histerese.
A teoria dos circuitos elétricos mostra que a energia W entregue por uma fonte a um circuito é:
t
W
t

v( t ) i(t ) dt 
0
d
 N dt i dt   N i d
0
(20.16)

Admitindo o circuito magnético com comprimento médio  e seção reta S uniforme temos:

W N

H
dBS   H  S dB   S H dB
N


B
(20.17)
B

Suponhamos que um material ferromagnético seja submetido à ação de um campo magnético H
variável no tempo, com uma frequência f ou período T = 1/f. Em cada ciclo ou período, uma parcela
da energia injetada no material será dissipada ou utilizada apenas para percorrer o ciclo de histerese
e se constituirá em perdas por histerese.
Para melhor compreendermos as perdas por histerese, vamos fazer uma análise passo a passo.
Denominando Ph a potência associada ao ciclo de histerese, e W h a energia dissipada em um ciclo,
ou período T teremos:
W h P h T 
Ph
f
(20.18)
Em termos de potência dissipada por histerese podemos então escrever que:
Ph  Wh f
(20.19)
2
Se o campo magnético é expresso em A/m e a indução magnética em tesla (T) ou Wb/m , a
densidade volumétrica de energia magnética wm, dada na equação (20.17), necessária para criar
uma indução magnética B é dada no Sistema Internacional por:
B
W 
w m  H dB  3 
m 
0

(20.20)
Neste caso, a energia magnética total armazenada no material de volume V é:
Wm  w m V
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
(20.21)
192
ELETROMAGNETISMO II
Vamos examinar agora graficamente a expressão para a densidade de energia ao longo de um ciclo
de histerese:
Se a curva é percorrida no sentido positivo (acréscimo na magnetização) como na figura 20.6, esta
área é algebricamente positiva e representa a energia entregue pela fonte ao material.
B (T)
H (A/m)
Figura 20.6: energia armazenada no material à medida que se aumenta a intensidade de
campo magnético
Pela figura 20.7, quando a curva é percorrida no sentido negativo (redução na magnetização) a área
é algebricamente negativa e representa a parcela de energia devolvida pelo material à fonte
externa.
B (T)
H (A/m)
Figura 20.7: energia liberada pelo material magnético, à medida que a intensidade de campo
magnético é reduzida
A diferença entre as áreas é a energia que foi dissipada na inversão dos domínios magnéticos no
material, em forma de calor.
B (T)
H (A/m)
Figura 20.8 – energia magnética perdida no aumento e redução de H
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
193
ELETROMAGNETISMO II
Fazendo essa análise ao longo de todo o ciclo de histerese, obteremos a perda por histerese em
um ciclo, que é a área do laço de histerese.
B (T)
H (A/m)
Figura 20.9 –energia dissipada em um ciclo de histerese
A energia dissipada W h em todo o material, ou seja, no volume V por ciclo é:
(20.22)
W h A V
onde A é a área do ciclo de histerese, e V o volume do material. Pela equação (20.19) a potência
devido ao fenômeno da histerese é então:
(20.21)
P h  A V f (W )
Exemplo 20.1
Seja um núcleo laminado de transformador, com chapas de espessura  = 1 mm, cuja liga de ferro
possui a curva mostrada na figura 20.10. Se o volume de material empregado no circuito magnético
7
é V = 100 cm 3, a condutividade do material é  = 10 S/m para uma freqüência elétrica f = 60 Hz,
calcule as perdas totais no ferro.
2
B (Wb/m )
1,5
0,98
H )A/m)
- 35
35 100
- 0,98
Figura 20.10 - Ciclo de histerese do exemplo 18.1
Solução:
a) cálculo das perdas por correntes
parasitas ou de Foucault:
A densidade volumétrica de potência
dissipada pelas correntes parasitas é
dada por
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino
194
ELETROMAGNETISMO II
pf 
Da mesma forma, temos que a potência
dissipada por unidade de volume por histerese
é dada pela área do ciclo, no caso calculada
de forma aproximada pelo paralelogramo:
2
Bmax
2  2
24
2

10 7.1,5 2.2 .60  . 10  3
pf 
24

2
A  2 Bmax 2 Hc (W/m3)
p f 1,33  105 W / m3
Logo, a potência dissipada pelas perdas
em histerese é dada por
E a potência dissipada por efeito Joule
neste caso resulta
Ph  2 Bmax 2 Hc V f
Pf  p f V  1,33  105.100  10 6  13,3 W
Ph  2 .1,5 . 2 . 35 .100 .10 6 . 60  1,3 W
Temos para o total das perdas no ferro
b) - cálculo das perdas por histerese
PFe  Pf  Ph  13,3  1,3  14,6 W
20.4 - Magnetoestrição
A Magnetostrição (ou magnetoestrição) é um fenômeno que certos materiais magnéticos apresentam
quando submetidos a tensões mecânicas (tração e compressão) modificando a arrumação de seus
dipolos magnéticos, produzindo deformações em suas dimensões. É um fenômeno de efeito análogo
ao piezelétrico no qual a pressão exercida provoca arrumação de dipolos elétricos, criando
diferenças de potencial.
A variação do comprimento do material, por unidade de comprimento, ao longo da direção do campo
é representada no gráfico da figura 20.11 à esquerda, para o ferro, níquel e cobalto. Valores altos de
H são necessários para produzir o mais alto efeito da magnetostrição. Alguns materiais, como o
níquel e o cobalto, se contraem na direção do campo magnético aplicado, (magnetoestrição
negativa) enquanto outros, como ligas permalloy, se alongam (magnetoestrição positiva) O níquel,
por exemplo, possui magnetoestrição negativa pois quando na presença de um campo H da ordem
de 50 A/m sofre uma redução da ordem de 0,002 % em seu comprimento.
Dl x10 -6
l
2
0 N/mm
20000
40000
60000
H (A/m)
0.50
2
10 N/mm
Fe
-10
Co
2
20 N/mm
0.25
-20
-30
500
1000
1500
-40
Ni
Figura 20.11 - Curva de magnetostrição para vários materiais ferromagnéticos
O efeito magnetostritivo é também reversível. Uma excitação mecânica modifica as propriedades
magnéticas do material enquanto que uma excitação magnética faz o material variar em suas
dimensões. Conforme pode ser visto no gráfico da figura 20.11 à direita. Inversamente, quando
submetido à compressão, o níquel melhora as suas propriedades ferromagnéticas.
Em máquinas elétricas, o fenômeno da magnetostrição é percebido através de ruídos durante a
operação das mesmas. Materiais magnetostritivos são utilizados na produção de ondas ultrassonicas
(sonar), filtros elétricos e medidores de deformação (transdutores em instrumentação).
UNESP/Bauru – Naasson Pereira de Alcantara Jr. – Claudio Vara de Aquino