tarefa1

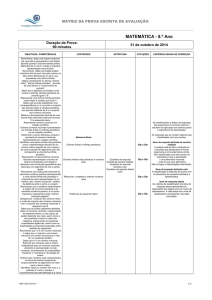
Tarefa 1 – Os números Irracionais
1- Considera os seguintes números:
1
2
00
8
2
-4

1
3
2
1
4
000
21
37
-8
0
2
5
6
22
7
Agrupa-os nos respectivos conjuntos.
IN

Q
Dizimas infinitas não periódicas
Sugestão: relativamente aos números fraccionários (representados por fracções) representa-os em forma de
dízima, ou seja, na calculadora efectua a divisão.
Nota: os números do conjunto, designado por outros, representam dizimam infinitas não periódicas. São
considerados os números ______________.
Um número irracional é um número cuja dízima é __________________________. Não pode ser
representado sob a forma de fracção.
Tarefa 1 +
2- Usando a calculadora
2.1. Representa por uma dizima cada um dos números e classifica-a.
7
5
17
c) 
9
a) 
e)
13
7
12
32
i)
99
312
l)
110
g)
n)
1
8
57
d)
11
b)
f)
h)
0,64
59
6
j)  7
m)
13
7
3
2
2.2. Relativamente às dízimas infinitas periódicas, indica o seu período.
2.3. Dos números anteriores indica quais são racionais e irracionais
3- Completa
Dízimas
Infinitas
Periódicas
Números Racionais
Números
Reais
Rei
4- Completa o quadro, marcando uma cruz quando o número pertence ao respetivo conjunto.
Números
Naturais
Inteiros
Relativos
Racionais Reais
×
5
3
16

×
5
20

10
0
-1,7
5- Completa-as de modo a obter afirmações verdadeiras, utilizando:
5.1.
Os símbolos de
 (pertence) e  (não pertence).
3..........N ;
 7.........N ;
7..........  ;
 4.........Z  ;
 1,5..........Z ;
0......... ;
16.........Z ;
 ......... ;
3
............Q ;
5
0,9..........Q ;
7........Q ;
0
......... 0 .
4
5.2. Os símbolos N , Z , Q ou 
5
 ..... ;
3
0,0003  .....; ;
 5  ..... ;
 9  ..... ;
 5,7  ..... ;
1,9  ..... .
6- Escreva:
6.1. Três números naturais maiores que 15;
6.2. três números inteiros consecutivos não naturais;
6.3. três números reais negativos e não inteiros;
6.4. três números reais positivos não racionais.
7- Diga, justificando, se são verdadeiras ou falsas as seguintes afirmações:
7.1. Todo o número real é racional.
7.2. Todo o número natural é inteiro.
7.3. Todo o número real é irracional.
8- O número
368
é um número racional. Confirma esta afirmação identificando o período da sua
491
dízima. Quantos algarismos tem?