Exemplo E.1.1. O bloco A de 600 kN desliza sobre rodas

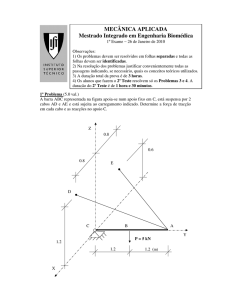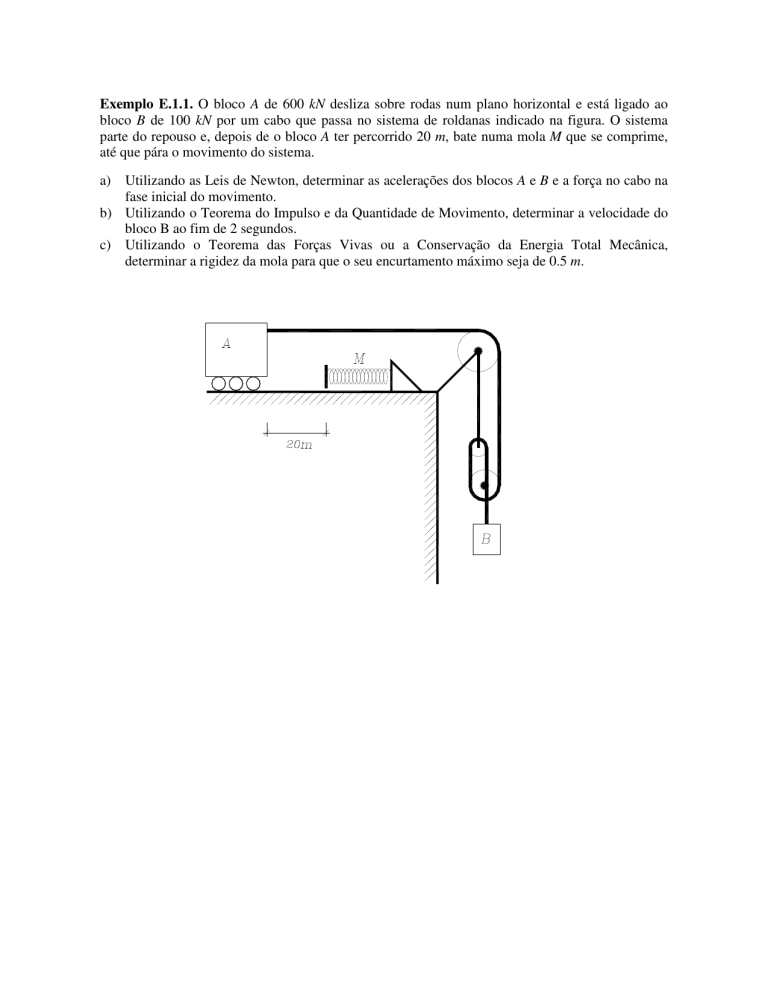
Exemplo E.1.1. O bloco A de 600 kN desliza sobre rodas num plano horizontal e está ligado ao
bloco B de 100 kN por um cabo que passa no sistema de roldanas indicado na figura. O sistema
parte do repouso e, depois de o bloco A ter percorrido 20 m, bate numa mola M que se comprime,
até que pára o movimento do sistema.
a)
Utilizando as Leis de Newton, determinar as acelerações dos blocos A e B e a força no cabo na
fase inicial do movimento.
b) Utilizando o Teorema do Impulso e da Quantidade de Movimento, determinar a velocidade do
bloco B ao fim de 2 segundos.
c) Utilizando o Teorema das Forças Vivas ou a Conservação da Energia Total Mecânica,
determinar a rigidez da mola para que o seu encurtamento máximo seja de 0.5 m.
Exemplo E.2.1. As partículas A e B, ambas de massa m, estão ligadas por uma barra rígida de peso
desprezável e de comprimento L. Num certo instante uma partícula C, igualmente de massa m,
atinge a barra AB a um quarto do seu comprimento medido a partir de B. A sua velocidade
(perpendicular à barra) é nesse instante igual a v e a partícula permanece ligada à barra após a
colisão. Todo o conjunto encontra-se sobre uma superfície horizontal sem atrito.
a) Calcule o momento linear e o momento angular do conjunto em relação ao seu centro de massa,
antes do choque.
b) Quais as velocidades das massas A, B e C imediatamente após o impacto?.
c) Calcule as velocidades das massas A, B e C após a barra ter rodado 180º.
m
-
L/4
x
C
A
L
v
m
B
m
Exemplo E.3.1. Considere a chapa triangular com massa por unidade de área ρ [ML−2] cujo tensor
de inércia foi calculado no exemplo E.2.4 dos apontamentos de CENTRO DE MASSA E TENSOR
DE INÉRCIA.
Se a chapa rodar com uma velocidade angular ω em torno de um eixo fixo que coincide com o eixo
dos xx da figura, determine:
a) A energia cinética da chapa.
b) O vector quantidade de movimento angular da chapa em relação ao ponto O.
Exemplo E.3.2. Considere-se o cilindro de massa M = 10 kg, raio R = 0.5 m e altura H = 2 m cujo
tensor de inércia foi calculado no exemplo E.2.7 dos apontamentos de CENTRO DE MASSA E
TENSOR DE INÉRCIA. O cilindro roda em torno de um eixo fixo z' que passa pelos pontos A, G e
B com velocidade angular ωz’ = 20 π rad/s.
a) Determinar a energia cinética do cilindro.
b) Determinar o vector quantidade de movimento angular em relação ao ponto G.
D
B
C
Exemplo E.3.3. O cilindro roda em torno de um eixo fixo z' que passa por G e pelos apoios C e D
com velocidade angular ω z’ = 20 π rad/s. Admitindo que a direcção y' é a direcção da gravidade (g)
e que a massa do eixo é desprezável, determine as reacções dinâmicas nos apoios C e D no instante
em que o cilindro passa pela configuração indicada. Admita que a distância de G a cada um dos
apoios é L/2, em que L = 4 m; admita ainda que o apoio C impede todos os movimentos de
translacção e que o apoio D permite a translacção segundo a direcção z'.
Exemplo E.3.4. Uma placa ABC com a forma de um triângulo rectângulo em A, pesando 600 N,
gira em torno do eixo y com velocidade e aceleração angulares que no instante considerado na
figura são de 35 rad/s e 80 rad/s2 respectivamente, ambas no sentido positivo do eixo. Determine:
a) O momento M aplicado na placa.
b) As reacções dinâmicas correspondentes em A e B (admita que o apoio A impede todos os
movimentos de translacção e que o apoio B permite a translacção segundo a direcção y).
z
C
0.6 m
1.0 m
-
x
A
x
M
B
y
Exemplo E.3.5. A figura representa um modelo biomecânico da cabeça e do pescoço de um
passageiro que está seguro ao banco de um automóvel. O conjunto cabeça mais metade do pescoço,
que se admite articulado no ponto A, tem uma massa M e um momento de inércia IG relativamente
ao eixo que passa no centro de gravidade. Se o automóvel e o tronco do passageiro são sujeitos a
uma desaceleração horizontal aA quando a cabeça está na posição indicada, determine as
componentes horizontal e vertical da força que o pescoço exerce na cabeça em A nesse instante. O
momento MA é o necessário para manter a cabeça na posição de equilíbrio não rodada indicada
antes da desaceleração. Admitir que o valor desse momento se mantém constante durante toda a
fase de desaceleração.
Exemplo E.3.6. A barra homogénea AB, representada na figura, tem peso P = 60 kN e
comprimento L = 0.8 m. As suas extremidades A e B deslizam sem atrito numa calha vertical e
numa calha horizontal, respectivamente. À extremidade A está ligada uma mola de rigidez k = 110
kN/m. Sabendo que o sistema parte do repouso quando θ = 60º e que a força na mola é nula quando
θ = 0º, determine:
a) a aceleração angular da barra e as acelerações dos pontos A e B no instante inicial quando
θ = 60º.
b) a velocidade angular da barra quando θ = 30º
θ
B
k
G
P
L
A
Exemplo E.3.7. O sistema representado na figura é constituído por um disco homogéneo de massa
M = 2 Kg e raio R = 10 cm, uma barra delgada AB de massa m = 0.5 Kg e comprimento L = 40 cm.
O disco rola sem escorregar sobre a superfície horizontal e a extremidade B da barra desliza sem
atrito numa guia vertical. O sistema é libertado do repouso quando θ = 45º. Considere que a
aceleração da gravidade g é de 10 m/s2.
a) Determine a aceleração do centro do disco no instante inicial.
b) Determine a velocidade do ponto B quando θ = 0º.
g
B
L
m
A
R
θ
M
Exemplo E.3.8. Um fio inextensível e sem massa enrola-se numa roldana dupla homogénea de
peso P. Na extremidade do fio está um peso A de valor 3P, apoiado numa mola de rigidez k que se
encontra indeformada na posição indicada na figura. Admitindo que se quebram as ligações CD e
EF, calcule o deslocamento de A no instante em que a sua velocidade passa pela primeira vez pelo
valor v.
2R
R
D
F
C
E
A
k
Exemplo E.3.9. A peça indicada na figura constituída por três discos concêntricos colados, é sujeita
à acção da força F através de um cabo enrolado no disco interior. O momento de inércia do
conjunto pode considerar-se igual a MR2/2. O coeficiente de atrito entre o solo e os discos é µ.
a) Qual o máximo valor de F para não haver escorregamento?
b) Na hipótese da alínea anterior (F ≤ Fmáx), e supondo que o sistema parte do repouso, qual a
velocidade de G ao fim do tempo t?
R
r
r
F
Exemplo E.3.10. Considere um bloco paralelepipédico ligado por uma barra rígida ao eixo de um
cilindro homogéneo, ambos de peso P. O coeficiente de atrito entre o bloco e o plano inclinado é µ
= 0.1. O cilindro rola sem deslizar. Partindo do repouso, quanto tempo é necessário para que o
bloco atinja uma velocidade v = 10 m/s?
β=30
Exemplo E.3.11. A partícula de massa m e velocidade v choca com a extremidade B da barra AB, a
qual tem massa M e comprimento L, está simplesmente apoiada em A e encontra-se inicialmente em
repouso. A seguir ao impacto a massa m adere à extremidade B da barra AB. Determine a menor
velocidade inicial v da massa m para que o conjunto venha a atingir a horizontal.
g
B
L
M
A
45º
v
m