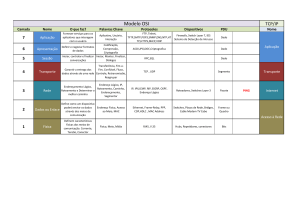
Minimizando Ramificações em Árvores Geradoras
Embora ainda não se conheçam algoritmos e_ficientes para resolvê-los,
problemas NP-difíceis estão com frequência presentes em situações reais que
demandam soluções rápidas, justifi_cando o interesse por métodos não exatos
como por exemplo heurísticas e algoritmos aproximativos. Uma dessas situações é
a alocação de switches WDM(Wavelength Division Multiplexing ) em redes ópticas.
Tais switches são dispositivos so_fisticados e caros, portanto minimizar a
quantidade desses equipamentos em uma rede torna-se desejável. O problema
estudado nessa tese foi assim de_finido: dado um grafo conexo G = (V, E ), não
direcionado e sem peso em suas arestas, encontrar uma árvore geradora T de G,
que possua a menor quantidade possível de ramifi_cações, ou seja, que minimize
em
T
o
número
de
vértices
v
com
grau
d
T (v) ≥ 3. Observe que nos casos em que esse número é zero, o problema consiste
em verifi_car se G é hamiltoniano. Nesse caso, seria encontrar uma solução ótima
para o problema, já que todos os vértices v de T teriam grau no máximo
igual a 2, de onde, por consequência, percebe-se a NP-di_culdade. Apresentamos
duas propostas baseadas em heurísticas, comparando nossos resultados com
aqueles obtidos pelas principais propostas encontradas na literatura, que utilizaram
heurísticas
e
algoritmo
aproximativo.
Palavras-chave: Grafos, Árvores Geradoras, Rami_ficações, Heurística,
Algoritmo Aproximativo.