EXERCÍCIOS DE RECUPERAÇÃO
Nome: ________________________________Nº_____
Profª CLAUDIA - 3º Bimestre - 8°Ano_____
DEVERÃO SER ENTREGUES APENAS OS EXERCÍCIOS: 4, 8, 9C, 10B, 11, 13, 16K, 16P, 19, 26
1. Neste mês, uma montadora produziu 787 carros, dos modelos clássico e esporte. A
produção do modelo esporte superou em 51 unidades a produção do modelo clássico.
Quantos carros de cada tipo foram produzidos?
2. Em um supermercado, foram vendidas 228 caixas de duas marcas de sabão em pó.
Lava Azul vendeu o triplo do que vendeu Lava Verde. Quantas caixas de cada marca
foram vendidas?
3. Uma classe tem 36 alunos. Há 8 meninas a mais que meninos. Quantos são os
alunos de cada sexo?
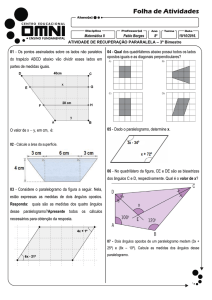
4. Na sua festa, Laís precisava acomodar 80 convidados em 22 mesas. Laurinha sugeriu
que colocasse algumas mesas com 3 lugares e outras com 4 lugares, de modo que
todos os lugares fossem ocupados pelos convidados. Quantas mesas ficaram com 3
lugares? Quantas com 4 lugares?
5. Em um sítio há marrecos e carneiros. No total, há 84 cabeças e 244 patas.
Quantos são os animais de cada espécie?
6. Os irmãos Marcos e Marlene ganham juntos R$1265,00 por mês. Marcos recebe
R$325,00 a mais que Marlene. Qual é o salário de cada um?
7. Em 2005, a população do Brasil era de aproximadamente 194 milhões de habitantes. A
população urbana era o triplo da população rural. Qual era a população urbana? E a
população rural?
8. Na 8º ano C há 32 alunos. Subtraindo o número de meninas do dobro do número de
meninos, o resultado é 7. Quantos são os meninos? E as meninas?
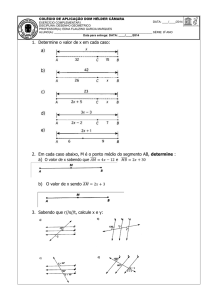
9. Resolva utilizando o método da substituição :
a) X + Y = 11
2X – 4Y = 10
b) X – 2Y = 0
7X + 11Y = 50
c) 2X + Y = -4
3X + 6Y = -15
d) Y = 2X -1
X = 7 – 3Y
10.Resolva utilizando o método da adição:
a) 2X + 3Y = 13
5X – Y = 7
b) 7P + 3Q = 12
5P + 2Q = 9
c) X – 3Y = 1
3X – 2Y = 4
d) 2X + Y = -4
3X + Y = -1
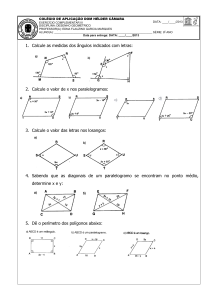
11.Quais são as medidas dos ângulos de um quadrilátero cujas medidas são expressas por
X + 250, 3X, X + 200 e 2X + 350?
12.Determine as medidas X e Y indicadas na figura abaixo:
13.As medidas de dois ângulos opostos de um paralelogramo são expressas por
4X + 1 e 6X – 21. Determine as medidas dos quatro ângulos do paralelogramo.
14. Determine as medidas x e y indicadas no retângulo abaixo.
15.Determine as medidas do ângulo agudo e do ângulo obtuso do trapézio retângulo da
figura.
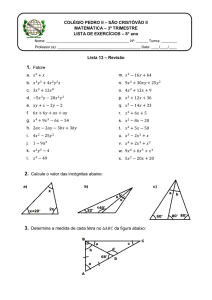
16. Fatore completamente
a) x³ - x
b) 4x²a - 16a³
e) 5x2 - 20
g) 8a3b – 18ab3
i) 27X2 – 36 X + 12
k) 72 X – 48 X2 - 27
m) -3X2 + 36X - 108
c) 2a² + 12a + 18
d) 5a² + 30ab + 45b²
f) 3Y2 – 3
h) 2x2 -16x + 32
j) – 6B – 9B2- 1
L) X5 – X3Y2
n) – 96X2 – 6Y2 + 48XY
o) 7X2 - 28
p) B4 – C4
q) x6 + 2x4 + ax² + 2a
s) by² - 2b + cy² - 2c
u) x³ - 10x² + xy - 10y
r) ax + 5x + ay + 5y
t) a³ - a² + a - 1
v) 10a³b - 5ab³ + 6a² - 3b²
17. A medida de cada ângulo obtuso de um losango é expressa por 2x + 5, enquanto a
medida de cada ângulo agudo é expressa por x + 40. Nessas condições, determine as
medidas dos quatro ângulos desse losango.
18.No trapézio isósceles, as diagonais medem respectivamente (2/3)x + 10 e 24 cm.
Determine o valor de x.
19.Um trapézio isósceles tem base média igual a x + 7, base menor x + 1 e base maior 26
cm. Calcule a medida da base média desse triângulo.
20.5. Um trapézio isósceles tem 124 cm de perímetro, e a base média mede 25 cm. Calcule
as medidas dos lados oblíquos desse trapézio.
21.6. Num trapézio isósceles a medida de um ângulo interno excede a de outra em 20 o.
Calcule os ângulos desse trapézio.
22.Uma diagonal de um paralelogramo forma 26o com um lado e 42o com o outro. Calcule as
medidas dos ângulos desse paralelogramo
23. Considere dois números inteiros, a e b, sabendo que
a2 – b2 = 39 e a – b = 3. Qual deve ser o valor de a + b?
24. Calcule o valor numérico da expressão 2mx – 5ny – 2nx + 5my sabendose que m – n = 4 e 2x + 5y = 15
25.Qual o valor numérico da expressão 2m + 2n, sabendo que m+n = 10?
26 . Calcule o valor numérico da expressão: xy³ + 7xy² - 3xy , sabendo-se que
xy = 6 e y² + 7y = 20.
27.Dado o polinômio x² – xz + 2xy – 2yz, calcule o valor numérico , sabendo
que x – z = 5 e x + 2y = 27
28. Sabe-se que 3x – y = – 12 e 3x + y = – 6. Nessas condições, qual é o valor
numérico da expressão 9x² – y²?
29. Fatore o polinômio x³y + 2x²y² + xy³ e determine o seu valor numérico,
sabendo que xy = 10 e x + y = –5
GABARITO
1. 419 do modelo esporte e 368 do modelo clássico
2. 171 caixas de Lava Azul e 57 caixas de Lava Verde
3. 14 meninos e 22 meninas
4. 8 mesas de 3 lugares e 14 mesas de 4 lugares.
5. 46 marrecos e 38 carneiros
6. Marcos R$795,00 e Marlene R$470,00.
7. PU- 145,5 milhões e PR- 48,5 milhões
8. 13 meninos e 19 meninas
9. a) X = 9; Y = 2 b) X = 4; Y = 2 c) X = -1; Y = -2
d) X = 10/7; Y = 13/7
10. a)X = 2; Y = 3 b) P = 3; Q = -3 c) X = 10/7; Y = 1/7 d) X = 3; Y = -12
11. 115o, 60o, 120o, 65o
12. X = 80o e Y = 50o
13. 45o, 45o, 135o, 135o.
14. x = 5o e y = 28o
15. agudo = 50o e o obtuso= 130o
16. a) x (x – 1) (x +1)
b) 4a (x – 2a) (x + 2a) c) 2 ( a + 3)2
d) 5 ( a + 3b)2
e) 5 (x – 2) (x + 2)
f) 3 ( Y – 1) ( Y + 1)
g) 2ab ( 2a+ 3b) ( 2a – 3b)
2
2
h) 2 ( x – 4 )
i) 3 ( 3X – 2)
j) -1 ( 3B + 1 )2
k) -3 ( 4X – 3)2
l) X3 (X + Y) (X – Y) m) – 3 ( X – 6)2 n) -6 ( 4X – Y)2 o) 7 (X +2) (x -2)
p) (B2 + C2) (B + C) (B – C)
q) (x² + 2)(x4 + a)
r) ( a + 5) (x + y)
s) (y² - 2 )(b + c)
t) (a² + 1)(a - 1)
u) ( x - 10)(x² + y)
v) (2a² - b²)(5ab + 3)
17. 95o , 95o, 85o e 85o
18. 21 cm
19. 20 cm
20. 37 cm ou 50 cm
21.100o e 80o 22. 112o e 68o
23. a) 13
27. 135
b) a = 8 e b = 5
28. 72
24. 60
29. 250
2 5. 20
26. 102