Feliz Ano-Novo - OMNI Educacional

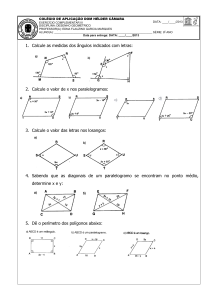
Matemática II
Pablo Borges
8º
19/10/2016.
ATIVIDADE DE RECUPERAÇÃO PARARALELA – 3º Bimestre
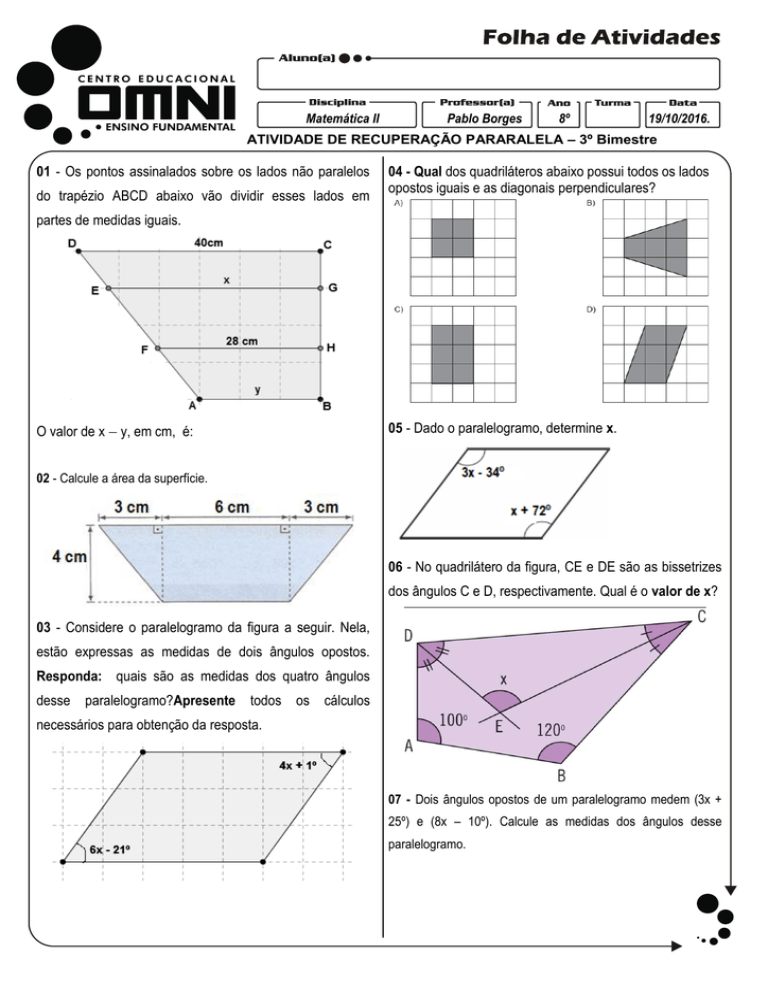
01 - Os pontos assinalados sobre os lados não paralelos
do trapézio ABCD abaixo vão dividir esses lados em
04 - Qual dos quadriláteros abaixo possui todos os lados
opostos iguais e as diagonais perpendiculares?
partes de medidas iguais.
O valor de x  y, em cm, é:
05 - Dado o paralelogramo, determine x.
02 - Calcule a área da superfície.
06 - No quadrilátero da figura, CE e DE são as bissetrizes
dos ângulos C e D, respectivamente. Qual é o valor de x?
03 - Considere o paralelogramo da figura a seguir. Nela,
estão expressas as medidas de dois ângulos opostos.
Responda: quais são as medidas dos quatro ângulos
desse paralelogramo?Apresente todos os cálculos
necessários para obtenção da resposta.
07 - Dois ângulos opostos de um paralelogramo medem (3x +
25º) e (8x – 10º). Calcule as medidas dos ângulos desse
paralelogramo.
08 - Dos ângulos internos de um trapézio medem 44º e
109º. Quais são as medidas dos outros ângulos internos
desse trapézio?
c) 8,5
d) 6,5
12 - No trapézio, a área mede 21 cm2 e a altura, 3 cm.
Então AB e DC valem, respectivamente:
09 - Nos trapézios abaixo, M e N são, respectivamente, os
pontos médios de AD e BC. Calcule o valor de x.
13 - Um terreno tem a forma de um trapézio retângulo
ABCD, conforme mostra a figura.
a) Determine a área do trapézio ABCD;
b) Se cada metro quadrado desse terreno vale
R$100,00, qual é o valor total do terreno?
10 - Calcule a área de um trapézio de bases medindo 10
cm e 5 cm e altura 6 cm.
14 - Dado o paralelogramo, determine x e y.
15 - A área do trapézio abaixo é 48 m2. A base AB = x + 4
11 - Um paralelogramo e um quadrado têm a mesma área.
Se o lado do quadrado mede 20 cm, e a base do
paralelogramo, 32 cm, então a medida da altura do
paralelogramo, em cm, é:
a) 12,5
b) 10,5
é igual a:
a) 12 m.
b) 10 m.
c) 25 m.
d) 6 m.