Geometria_-_respostas_-_aula_01

GEOMETRIA – AULA 01 – Soluções (POTI – Pirassununga)
Prof. Antonio
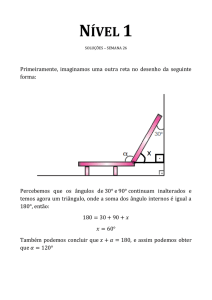
1. Na próxima aula (tarefa).
2. Do triângulo STU temos que TŜU =180°- (75° + 30°)=75°. Logo, esse
triângulo é isósceles (por ter dois ângulos iguais) e portanto TU=SU. Como
TU=SV, segue que SU=SV. Portanto, o triângulo SUV também é isósceles e,
̂ V = SV
̂U, então:
portanto, o ângulo SU
̂U = 180° − 50° → 2SV
̂U = 130° → SV
̂U = 65°
2SV
3. O triângulo ABE é isósceles porque tem dois ângulos iguais.
Logo os lados AE e AB são iguais,
portanto AB=120m. O triângulo BCD
também é isósceles porque tem dois
̂ C = BĈD.
lados iguais, BC=BD, logo BD
̂ C = BĈD, então os três ângulos
Como DB
do triângulo BCD são iguais, logo cada
um vale 180º ÷ 3 = 60º . Assim, ele é
equilátero e temos BD=BC=CD=115m.
Assim, o perímetro da figura é: 120 × 2 + 115 × 2 + 226 = 696m.
4. O triângulo KLM é isósceles porque tem dois lados Iguais KL=KM;
̂L = α .
consequentemente seus ângulos da base são iguais, isto é: KL̂M = KM
̂S = β.
Analogamente, o triângulo KST também é isósceles, portanto, KŜT = KT
̂ T = 𝑦 e ST
̂M = 180° − β, então:
Sejam: SK
• No triângulo STM temos: x +α +180° − β =180° ⇒ x = β − α
• No triângulo KLM temos: α +α + 30° + y =180° ⇒ y =150º − 2α
• Pelo triângulo KST temos: β + β + y =180° ⇒ β + β + 150° − 2α = 180° ⇒
2β − 2α = 30° ⇒ β − α =15° . Portanto, x =15°.
⇒
5. Completamos a figura marcando os ângulos α e β, lembrando que ângulos
opostos pelo vértice são congruentes (iguais).
Como a soma dos ângulos internos de um
triângulo é 180°,
podemos escrever as três igualdades abaixo,
uma para cada um dos triângulos da figura:
α + 7x = 180°
β + 8x = 180°
α + β + 5x = 180°, logo:
(α + 7x) + (β + 8x) − (α + β + 5x) = 180° + 180° − 180°
α + 7x + β + 8x −α − β − 5x = 180°
10x = 180°, então x = 18°
6. O ângulo 𝐸𝐴̂𝐵 = 108° (A medida do ângulo interno de um polígono regular
de n lados é obtida dividindo-se a soma dos ângulos internos por n, ou seja,
𝑎𝑖 = ⌈(𝑛 − 2). 180°⌉/𝑛)
O ângulo 𝐸𝐺̂ 𝐹 = 60° (Triângulo equilátero)
Pelo triângulo EAG, temos
𝐴𝐸̂ 𝐺 + 60° + 108° = 180°, logo: 𝐴𝐸̂ 𝐺 = 12°
7. Sejam x e y as medidas dos ângulos em branco e cinza, respectivamente,
como mostra a figura:
Pelo teorema do ângulo externo no triângulo BCD, temos
𝑦 + 𝑏 = 𝑥
Somando os ângulos do triângulo ABC, obtemos
60° + 2𝑦 + 180° − 2𝑥 = 180°
60° + 2𝑦 = 2𝑥 , dividindo por 2, temos: 30° + 𝑦 = 𝑥
Então:
𝑦 + 𝑏 = 30° + 𝑦 ⇒ 𝑏 = 30°
̂D = CD
̂ E = 𝑥. Então: 2𝑥 + 20° = 180° ⇒ 𝑥 = 80°
8. Como EDC é isósceles, CE
̂
̂
Como BEC é isósceles BCE = CBE = 𝛽. Usando ângulo externo, temos que
̂ E = 𝛼.
2𝛽 = 𝑥 = 80° ⇒ 𝛽 = 40°. Como ABE também é isósceles, BA
Finalmente, usando mais uma vez ângulo externo, temos: 2𝛼 = 180° − 𝑥 ⇒
⇒ 2𝛼 = 180° − 80° ⇒ 2𝛼 = 100° ⇒ 𝛼 = 50°.
Logo a razão
𝛼
𝛽
=
50°
40°
=
5
4
9. Como o triângulo é isósceles concluímos que,
̂ C, então temos:
̂ M = AB
̂ M = α e AĈB = BA
CB
2AĈB + 2α = 180° ⇒ AĈB + α = 90° ⇒ AĈB = 90° − α
Pelo triângulo AQC, segue:
̂ Q + AĈQ + AQ
̂ C = 180° ⇒ CA
̂ Q + 90° − α + 90° = 180°
CA
̂ Q = α.
⇒ CA
̂ Q = α e HA
̂ I = α (enunciado), então CA
̂ I = 2α e
Como CA
̂ B = 2α, pois AI é bissetriz de BA
̂ C.
IA
Finalmente no  AMB, temos:
̂ H + HA
̂ I + IA
̂ B + AB
̂ M = 90°
MA
α + α + 2α + α = 90°
5α = 90° ⇒ α = 18°