prof.ª dheyza pinto de carvalho prof. ivair nascimento taveira

MATEMÁTICA
9° ANO
ENSINO FUNDAMENTAL
PROF.ª DHEYZA PINTO DE CARVALHO
PROF. IVAIR NASCIMENTO TAVEIRA
CONTEÚDOS E HABILIDADES
Unidade II
Geometria
2
CONTEÚDOS E HABILIDADES
Aula 18.2
Conteúdos
•• Quadrados
•• Trapézios: Trapézio Retângulo, Trapézio Isósceles e
Trapézio Escaleno.
3
CONTEÚDOS E HABILIDADES
Habilidades
•• Aprender a calcular a área e a diagonal do quadrado.
Verificar as propriedades.
•• Conhecer os tipos de trapézios. Aprender a calcular a área
do trapézio.
4
AULA
Quadrado
Propriedades
Além das propriedades do paralelogramo o
quadrado possui as seguintes propriedades:
P1) Os quatro lados são congruentes.
P2) As diagonais são bissetrizes de seus vértices.
P3) As diagonais são perpendiculares entre si.
P4) As diagonais são congruentes.
P5) Os quatro ângulos são retos.
5
AULA
Área e diagonal
Todo quadrado é um retângulo. Então sua área é calculado
da mesma forma, multiplicando seus lados.
A = l²
l
l
6
AULA
Para encontrar a diagonal aplicamos o teorema de Pitágoras.
d² = l² + l²
d² = 2l²
d=
2l²
d=l 2
7
AULA
Circunferência inscrita e circunscrita no quadrado
�= l
2
R= d
2
8
DINÂMICA LOCAL INTERATIVA
1. Calcule a área e a diagonal de um quadrado de lado igual
a 8 cm.
2. Um quadrado tem 400 m² de área. Qual a medida de seus
lados?
9
INTERATIVIDADE
1. Calcule a área e a diagonal de um quadrado de lado igual
a 8 cm.
2. Um quadrado tem 400 m² de área. Qual a medida de seus
lados?
10
AULA
Trapézios
O trapézio é um quadrilátero
convexo que possui dois lados
paralelos.
B e b - bases (paralelas) do
trapézio
h - altura do trapézio (distância
entre as bases)
11
AULA
Propriedades em relação aos ângulos do trapézio
P1) Dois ângulos consecutivos porém em bases diferentes
são suplementares, ou seja, a sua soma é igual a 180º.
12
AULA
Classificação:
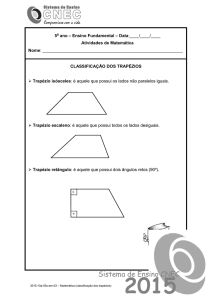
•• Trapézio Isósceles - é aquele que possui os lados
oblíquos congruentes
13
AULA
•• Trapézio Retângulo - é aquele que possui dois ângulos
retos, 90º.
14
AULA
•• Trapézio Escaleno - é aquele que os lados não paralelos
não são congruentes.
15
AULA
Área
Um trapézio é formado por uma base maior (B), por uma
base menor (b) e por uma altura (h).
Para fazermos o cálculo da área do trapézio é preciso
dividi-lo em dois triângulos, veja como:
16
AULA
Primeiro: completamos as alturas no
trapézio:
Segundo: o dividimos em dois
triângulos:
A área desse trapézio pode ser
calculada somando as áreas dos
dois triângulos (∆CFD e ∆CEF).
Antes de fazer o cálculo da área
de cada triângulo separadamente
observamos que eles possuem
bases diferentes e alturas iguais.
17
AULA
Cálculo da área do ∆CEF:
A∆1 = B . h
2
Cálculo da área do ∆CFD:
A∆2 = b . h
2
18
AULA
Somando as duas áreas encontradas, teremos o cálculo da
área de um trapézio qualquer:
AT = A∆1 + A∆2
AT = B . h + b . h
2
2
AT = h (B + b)
2
19
DINÂMICA LOCAL INTERATIVA
A base maior de um trapézio isósceles mede 14 m e a base
menor 8 m. Calcule a área do trapézio sabendo que a sua
altura é de 2m.
2m
20
INTERATIVIDADE
A base maior de um trapézio isósceles mede 14 m e a base
menor 8 m. Calcule a área do trapézio sabendo que a sua
altura é de 2m.
2m
21
RESUMO DO DIA
Quadriláteros
1) Paralelogramo
A = b.h
22
RESUMO DO DIA
2) Retângulo
A= a.b
d² = a² + b²
23
RESUMO DO DIA
3) Quadrado
A = l²
d=l 2
24
RESUMO DO DIA
4) Trapézio
Isósceles - aquele que possui os
lados oblíquos congruentes
Retângulo - aquele que possui
dois ângulos retos.
25
RESUMO DO DIA
Escaleno - aquele que os lados não paralelos não são
congruentes.
Área do trapézio
A = h (B + b)
2
26