2º Teste / 1º Exame de Transmissão de Calor

2º Teste/1º Exame de Transmissão de Calor
Mestrado Integrado em Engenharia Mecânica e
Engenharia Aeroespacial
11 de Janeiro de 2010
1º Semestre
Observações:
1- Duração do teste: 2h; duração do exame: 3 h
2- Tempo aconselhado para a parte teórica: 40 minutos (teste) a 1 hora (exame)
3- Não é permitida consulta na parte teórica nem a utilização de máquina de calcular
A parte teórica é para ser respondida no enunciado. Identifique-o:
Número:
Curso:
Nome:
.
.
Parte Teórica (8 valores)
2º Teste – Questões 3, 4, 5, 6, 8 e 9
1º Exame – Questões 1, 2, 3, 4, 7 e 9
Para as questões 1 a 6 são indicadas quatro afirmações. Indique se cada uma dessas
afirmações é verdadeira (V) ou falsa (F). Cada resposta certa conta 0.25 valores e cada
resposta errada desconta 0.20 valores, sendo que a cotação do conjunto destas questões nunca
será inferior a 0.
1 a 6 – questões não disponibilizadas
7.
Num cabo condutor de corrente eléctrica, longo, suspenso entre dois suportes, há
libertação de energia por efeito Joule. Seja Tb a temperatura do cabo nos suportes e T a
temperatura ambiente. A distribuição da temperatura na vizinhança de um suporte, em
regime estacionário, é descrita pela seguinte equação
d2
dx
2
 m2  
q
0
k
em que (x) = T(x) - T e m 2  h P k Ac  , sendo h o coeficiente de convecção, k a
condutibilidade térmica do material, Ac a área da secção transversal, P o respectivo
perímetro e q a potência libertada por unidade de volume por efeito Joule. (2 val.)
(a) Longe dos suportes, a temperatura do cabo é uniforme. Determine essa temperatura.
(b) Determine a distribuição da temperatura no cabo na vizinhança de um suporte.
8.
Numa cavidade de comprimento L e altura H, cujas superfícies horizontais são
adiabáticas, a superfície do lado esquerdo é mantida a uma temperatura quente, Th, e a do
lado direito a uma temperatura mais baixa, Tc. Suponha que o modo de transmissão de
calor dominante é a convecção natural, em regime laminar. (2 val.)
(a) Represente graficamente uma evolução plausível
da componente v da velocidade na secção (x, H/2)
para 0  x  L.
(b) Represente graficamente uma evolução plausível
da temperatura na secção (x, H/2) para 0  x  L.
(c) Represente graficamente uma evolução plausível
da componente u da velocidade na secção (L/2, y)
para 0  y  H.
(d) Represente graficamente uma evolução plausível
do número de Nusselt ao longo da parede quente
(0, y) para 0  y  H.
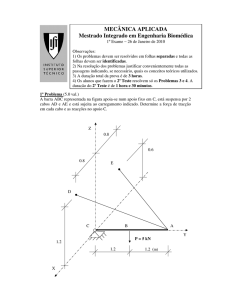
9. Determine o factor de forma da superfície 1 (lado de um quadrado de lado L) para a
superfície 2 (circunferência de diâmetro D) em função de L e de D. Os centros do
quadrado e da circunferência são coincidentes. A dimensão perpendicular ao papel
pode ser tratada como infinita.
2º Teste / 1º Exame de Transmissão de Calor
Mestrado Integrado em Engenharia Mecânica e
Engenharia Aeroespacial
11 de Janeiro de 2010
1º Semestre
Observações:
1- Duração do teste: 2h; duração do exame: 3 h
2- A parte prática é com consulta limitada a um livro de texto ou a apontamentos da
disciplina. Não é permitida a consulta a problemas resolvidos.
Parte Prática (12 valores)
Resolva os seguintes problemas em folhas separadas:
2º Teste –
Problema 2 (6 val)
Problema 3, alíneas a, b, d, e (6 val)
1º Exame – Problema 1 (4 val.)
Problema 2, alíneas a, b, c (4 val.)
Problema 3, alíneas a, b, c (4 val.)
1.
Considere o tubo esquematizado na figura no interior do qual se escoa um caudal de 0,01
kg/s de gás natural proveniente de um reservatório de gás natural liquefeito e que está a
ser aquecido para ser alimentado a uma rede de distribuição. Pretende-se calcular a taxa
de transferência de calor por unidade de comprimento do tubo numa secção onde o gás
natural se encontra a -50 ºC e a temperatura exterior do tubo é de -40 ºC. O tubo é de
alumínio (k = 200 W/(m.K)) e possui oito alhetas interiores longitudinais, conforme a
geometria indicada na figura.
30 mm
Diâmetro interior de 26 mm e
alhetas interiores com altura
de 6 mm e espessura de 2 mm
Considere as seguintes propriedades para o gás natural à temperatura de -50 ºC:
 = 8,5 x10-6 kg/(m.s); k = 0,024 W/(m.K); cP = 2500 J/(kg.K); Pr = 0,73.
(a) Calcule o coeficiente de convecção entre o gás natural e a superfície interior do tubo
e alhetas considerando a situação de temperatura imposta. (2 val.)
(Se não resolver considere h = 170 W/(m2.K) para a alínea seguinte)
(b) Calcule a eficiência das alhetas e a taxa de transferência de calor por unidade de
comprimento do tubo. (2 val.)
2.
Considere um permutador de calor tubular para refrigerar água num escoamento de ar. A água
escoa-se nos tubos e o ar escoa-se por fora, em escoamento cruzado. A água entra a 80 ºC e sai
a 50 ºC com um caudal mássico de 0,5 kg/s, o ar entra a 10 ºC e o respectivo caudal mássico é
2,1 kg/s. A área da superfície exposta do permutador é 58,3 m2 e o coeficiente global de
transmissão de calor é 40 W/(m2.K).
(a) Calcule a temperatura de saída do ar. (0.5 val)
(b) Calcule as temperaturas de saída do ar e da água num
permutador de calor de área equivalente e o mesmo coeficiente
global de transmissão de calor mas em contra-corrente. (2 val)
(c) Compare qualitativamente, num mesmo gráfico, a evolução de
temperatura da água entre a entrada e a saída: (1.5 val.)
(i) no permutador em contra-corrente
(ii) num tubo do lado da saída do ar, no permutador em escoamento cruzado
(iii) num tubo do lado da entrada do ar, no permutador em escoamento cruzado
(d) Calcule o coeficiente de transmissão de calor por convecção no interior dos tubos, por
onde circula a água. assumindo que o diâmetro interno dos tubos é igual a 5 mm e a
velocidade média da água é 2 m/s. Admita que o comprimento de cada tubo é muito maior
que o seu diâmetro. (2 val.)
3.
Pretende-se estimar a taxa de transferência de calor de uma pessoa numa sala na presença de
um aquecedor de parede com 0,75 m de altura e 0,6 m de largura, conforme indicado na figura.
A pessoa é aproximada por duas placas paralelas verticais, representando a frente e as costas,
com dimensões de 0,6 m de largura e 1,5 m de altura. Considere como conhecidos os valores
das temperaturas seguintes: exterior da roupa 28 ºC, aquecedor 50 ºC, todas as outras
superfícies na sala 17 ºC, ar no interior da sala 20 ºC. Considere a emissividade da roupa como
0,7 e que todas as outras superfícies se comportam como corpos negros.
(a) Calcule o factor de forma entre o aquecedor e a pessoa e o inverso entre a pessoa e o
aquecedor (Não esquecer que esta é simulada por duas placas em direcções opostas; se não
calcular considere os valores FAP = 0,06 e FPA = 0,015). (1.5 val.)
(b) Apresente o análogo eléctrico que representa as trocas de calor entre as três superfícies
identificadas: pessoa, aquecedor e restantes superfícies da sala. (1 val.)
(c) Calcule a taxa de transferência de calor por radiação a partir da pessoa. (1.5 val.)
(d) Calcule o coeficiente de convecção natural da pessoa para o ar na sala. (2 val.)
(Se não resolver esta alínea considere o valor de 3 W/(m2.K) para a alínea seguinte).
(e) Calcule um novo valor para a temperatura exterior da roupa considerando que o calor é
transferido da pele a 34ºC, através da roupa, com uma resistência térmica de 0,1 m2.K/W,
para o ambiente, por convecção e radiação em paralelo. A troca de calor por radiação pode
aproximar-se por q”= hrad (TRoupa-TRadiante) com hrad = 4 W/m2K e TRadiante = 17,6 ºC. (1.5
val.)