Baixar o arquivo - Filosofia e Psicologia na ESARS

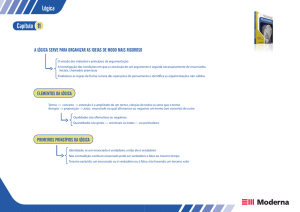
Formas de inferência válida ou regras da lógica proposicional
 Como qualquer disciplina/ciência a lógica formal, no estudo do seu objeto (argumentos dedutivos), também tem por
missão chegar a constantes: regras/leis/normas
 No caso da lógica formal, as constantes são as regras ou leis que permitem obter argumentos dedutivos válidos.
 Usando qualquer destas regras podemos estar certos de partindo das premissas verdadeiras obter uma conclusão
que não é falsa.
 Qualquer violação a estas regras resulta num argumento dedutivo inválido ou falácia formal.
 Falácia formal:
o Argumento que parece, formalmente, válido (semelhante a uma forma válida), mas que é inválido uma vez
que viola regras de inferência válida.
o Argumento em que a conclusão não decorre necessariamente das premissas.
o Argumento que, num inspetor de circunstâncias, apresenta sempre, pelo menos, uma circunstância em que as
premissas são verdadeiras e a conclusão falsa.
As formas de inferência válida que vamos estudar permitem duas coisas:
 Avaliar a validade (se é válido ou inválido) de alguns argumentos sem recurso às tabelas de verdade e aos inspetores
de circunstâncias.
 Construir os nossos próprios argumentos validamente, extraindo conclusões com base em determinadas premissas.
Formas de inferência válida
Modus Ponens
P→ Q
P
___________
Q
Falácia formal correspondente
Falácia da afirmação do consequente
P→ Q
Q
_________
P
Falácia da negação do antecedente
Modus Tollens
P→ Q
¬Q
_______
¬P
P→ Q
¬P
________
¬Q
Formas de inferência válida
Falácia
Faláciaformal
formalcorrespondente
correspondente
Contraposição
P→ Q
________
¬Q → ¬P
Exemplo
Falácia da inversão do condicional
P→ Q
________
Q→ P
Se a Ana vive em Lisboa, então vive em Portugal
___________________________________________
Se a Ana não vive em Portugal, então não vive em Lisboa
Exemplo
Silogismo
hipotético
P→ Q
Q →R
_______
P→ R
Se o tubarão é um peixe, respira por guelras
Se respira por guelras, então vive no mar
____________________________________
Se o tubarão é um peixe, então vive no mar
Silogismo
disjuntivo
(inclusivo)
1ª Lei de De
Morgan
Exemplo
PvQ
¬P
___________
Q
Formas de inferência válida
¬ (P ^ Q)
__________
(¬ P v ¬ Q )
O João vai ao cinema ou à biblioteca
Ora é falso que o João vá à biblioteca
_______________________________
O João vai ao cinema
Exemplos
É falso que o tubarão seja um mamífero e respira por
guelras
_____________________________________________
O tubarão não é um mamífero ou não respira por
guelras
2ª Lei de De
Morgan
¬ (P v Q)
__________
(¬ P ^¬Q)
É falso que o tubarão seja um mamífero ou respira por
guelras
____________________________________________
O tubarão não é um mamífero e não respira por
guelras