Vetores e Cinemática Vetorial II - Portal

“Sobre ombros de gigantes”
EQUIPE DE FÍSICA-1º ANO/CMB
Profs. Adameck, Eliete, SO Antônio Marcos & Luciano
VETORES E CINEMÁTICA VETORIAL II
1) Analise as proposições a seguir e determine quais são corretas e a erradas:
a( ). Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória pode ser
retilínea, mas não necessariamente.
b( ). Para que a velocidade vetorial de um corpo permaneça constante, ele deve se mover em
MRU.
c( ). Duas pessoas sentadas em um mesmo automóvel podem estar se deslocando em relação à
estrada com diferentes velocidades lineares.
d( ). Quando o módulo da velocidade de um móvel for constante, esse móvel não possui
aceleração.
e( ). Enquanto a aceleração vetorial de um móvel permanece constante, não pode haver alteração
na direção da velocidade vetorial.
2) (PUC-MG-Adap.) As figuras mostram reproduções de três fotografias estroboscópicas, cada uma
correspondendo ao movimento de uma partícula em um plano. Em todas as fotos, duas posições
sucessivas da partícula correspondem sempre a um mesmo intervalo de tempo, a saber 0,1 segundo.
Sobre estas situações julgue os itens que se seguem:
Situação A
Situação B
Situação C
a( ). Na situação A, a velocidade vetorial é constante.
b( ). A aceleração vetorial na situação B é nula.
c( ). Na situação C a velocidade vetorial não é constante, pois o móvel executa um movimento
curvilíneo.
1
d( ). Na situação C, a aceleração vetorial é constante, pois o móvel executa um movimento
circular uniforme.
e( ). Na situação B, o móvel possui velocidade vetorial constante, pois o móvel descreve espaços
iguais em intervalos de tempos iguais.
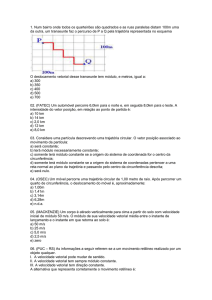
3) (ITA-2007-Adap.) A figura mostra uma pista de corrida A B C D E F, com seus trechos retilíneos e
circulares percorridos por um atleta desde o ponto A, de onde parte do repouso, até a chegada em F,
onde para. Os trechos BC, CD, e DE são percorridos com a mesma velocidade de módulo constante.
Com base no texto, julgue os itens que se seguem:
a( ). O atleta completa o trecho BC com velocidade escalar constante. Logo, não existe aceleração
atuando no movimento do atleta no referido trecho.
b( ). No trecho AB, o atleta desenvolve um movimento retilíneo uniforme.
c( ). O sentido da aceleração vetorial média do movimento do atleta é o mesmo nos trechos AB e
EF.
d( ). O movimento do atleta é acelerado nos trechos AB, BC, DE e EF.
e( ). O sentido da aceleração vetorial média do movimento do atleta é para sudeste no trecho BC,
e, para sudoeste, no DE.
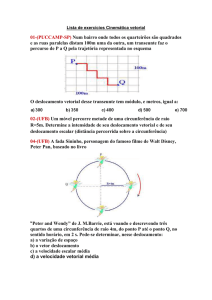
4) (UFC-2003-Adap.) A figura a seguir mostra o mapa de uma cidade em que as ruas retilíneas se
cruzam perpendicularmente e cada quarteirão mede 100 m. Você caminha pelas ruas a partir de sua
casa, na esquina A, até a casa de sua avó, na esquina B. Dali segue até sua escola, situada na esquina C.
E logo em seguida retorna a casa de sua avó e depois segue até o mercado na esquina D.
C
B
𝑃⃗2
𝑃⃗1
A
𝑃⃗3
Com base no texto e na figura, julgue os itens que se seguem:
2
D
a( ). O vetor posição P1 possui módulo 200 m.
b( ). O vetor deslocamento BC possui módulo igual a 100√29 𝑚;
c( ). Sabendo que no deslocamento BD, o tempo gasto na sua caminhada foi de 10 min, então o
módulo de sua velocidade vetorial média é aproximadamente 0,9 m/s.
d( ). No deslocamento BC, o tempo gasto na sua caminhada foi de 300 s, logo sua velocidade
vetorial média tem o módulo de √29 3 m/s e a orientação é de C para B.
e( ). A distância de A para C é de 1100 m, em linha reta.
5) (EN) Um móvel desloca-se em uma trajetória retilínea e na direção do eixo Ox, de tal maneira que
sua velocidade 𝑣 varia com o tempo (t) de acordo com a equação:
𝑣 = 4𝑡 − 8 𝑖
O 𝑖
0
1
2
x(m)
Em que t é dado em segundos, v em metros por segundo e 𝑖 é o versor mostrado na figura. Sabendo
que para t = 1 s o vetor posição da partícula (cuja origem está em O) é dado por 𝑟 = 2𝑖 (com 𝑟 em
metros), determine:
(a)
(b)
(c)
(d)
O vetor posição da partícula no instante t = 0;
O vetor posição da partícula no instante t = 6 s;
O módulo do vetor deslocamento entre os instantes t = 0 e t = 6 s;
A distância total percorrida entre os instantes t = 0 e t = 6 s.
6) Uma roda gigante com raio de 14 m está girando em torno de um eixo horizontal passando pelo seu
centro (figura abaixo). A velocidade linear de uma passageira em sua periferia é igual a 3,00 m/s, no
ponto A. Sabe-se que no deslocamento de A para B, a roda levou 2 s.
𝑣𝐵
B
𝑣𝐴 = 3 𝑚 𝑠
A
Determine:
a) O módulo a direção e o sentido do vetor deslocamento de AB.
3
b) Sabendo que a aceleração vetorial média tem módulo de 2,5 m/s2, determine o módulo do
vetor velocidade no ponto B.
c) Encontre o módulo da aceleração centrípeta nos pontos A e B.
GABARITO
1)
2)
3)
4)
5)
6)
E; C; C; E; E
C; E; C; E; E
E; E; C; C; C
E; C; E; E; E
a) 𝑟0 = 8𝑖; b) 𝑟 = 32𝑖; c) 24m d) 40 m
a) 14√2 𝑚, direção da reta que vai do ponto A até o ponto B e sentido de A para B.
b) 𝑣𝐵 = 4 𝑚 𝑠; c) 𝑎𝑐𝑝𝐴 =
9
14
𝑚 𝑠 2 e 𝑎𝑐𝑝𝐵 =
16
14
4
𝑚 𝑠2