Calor - Engenharia Fácil

Calor
INTRODUÇÃO
Para iniciar nossos estudos sobre a calorimetria é necessário, de início, diferenciar três coisas que
muitos confundem na hora das provas. Temperatura, Calor sensível e Calor latente.
Vamos distinguir Temperatura X Calor (de uma forma geral):
Como vimos na apostila passada, temperatura é o grau de agitação das moléculas, representado
pelas unidades que já estamos carecas de saber -> Kelvin, Graus Celsius, Graus Fahrenheit.
Calor envolve energia. Tanto que pode ser chamado de Energia Térmica em movimento.
Calor é a energia que é transmitida do corpo mais quente para o mais frio, devido a essa diferença
de temperatura. Sua unidade, como esperado, é unidade de energia-> Joule, ou caloria (faremos
sua relação mais a frente) ;D
1 TIPOS DE CALOR
Agora, vamos distinguir os tipos de Calor, o sensível e o latente:
Calor sensível é o que altera a temperatura dos corpos, ou seja, ao aproximarmos dois
corpos com temperaturas diferentes, ocorre um fluxo de calor sensível entre os corpos, que faz
com que a temperatura do mais frio aumente e que a do mais quente diminua. Até que, por fim,
suma essa diferença de temperatura.
Calor latente é o que causa mudança de fase, ou seja, é a energia necessária para que um
corpo passe de um estado físico para outro. Solido-> liquido; liquido-> gasoso; (...). É bem fácil de
perceber que o calor latente não provoca aumento de temperatura.
Você pode observar esses conceitos em casa!
Coloque água para ferver e coloque dentro dela um termômetro (cuidado para não
se queimar!!). Inicialmente verá que a temperatura da água irá subir, até atingir o ponto de 100°C,
depois, não importa quanto tempo você deixe a água esquentando, sua temperatura não passará
de 373 K.
Quando a água aumenta de temperatura, significa que o fogo está transferindo
energia para a água, sob forma de Calor sensível, quando a temperatura da água para de subir e ela
começa a vaporizar, o fogo transfere energia sob forma de Calor latente.
Definições importantes
Como geralmente acontece nas áreas de estudo provadas experimentalmente, teremos que
definir algumas fórmulas e conceitos que não possuem uma própria demonstração matemática,
vamos nessa:
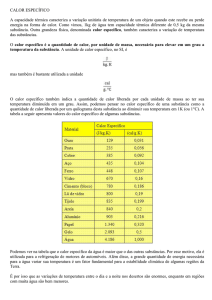
Caloria (cal): É a unidade (não é S.I.) de calor. Foi definida como: a energia necessária para elevar
de 14,5°C para 15,5°C, 1g de água.
A caloria é relacionada com o Joule (pertence ao S.I.) da seguinte maneira:
Calor específico (c):
Experimentalmente, foi observado que a energia necessária ( ) para elevar
substancia em uma temperatura
é calculada da seguinte forma:
gramas de uma
(1)
O coeficiente “ ” é o chamado calor específico da substancia, sua unidade é ”
”.
Obs.: Para ser rigorosos, não podemos considerar que o calor específico de uma substancia é uma
constante. Na verdade teríamos que dizer que
, pois o calor específico de uma substancia
varia com a temperatura, fazendo com que a equação (1) fique assim:
(1.1)
Contudo essa variação é bastante pequena a não ser para variações enormes de temperatura,
ou seja, para os problemas que resolveremos, podemos usar a formula (1).
Capacidade Térmica (C):
Chamamos de capacidade térmica o produto calor específico e massa.
(1) em:
(2)
. Transformando
Muitas vezes é mais interessante escrever a capacidade térmica sob a forma de capacidade térmica
molar, para descobrir a quantidade de energia necessária para mudar a temperatura de 1mol de
substancia. Para chegarmos na cap. térm. molar fazemos:
Calor latente (L):
De forma similar a feita em (1.2) estudiosos chegaram a formula que determina quanta energia é
necessária para mudar de estado gramas de uma substancia:
(3)
Essa constante é o chamado calor latente e depende exclusivamente do material e dos estados
que estão mudando, ou seja, existe para a água, por exemplo, o Calor Latente de Fusão , calor
latente de vaporização .
Outra coisa que vale a pena lembrar é que transformações opostas, como liquefação e fusão, ou
condensação e vaporização, possuem um mesmo calor latente, uma vez que acontecem a mesma
temperatura #fikadik.
Reservatório Térmico
São chamados de reservatórios térmicos os sistemas que permitem a troca de energia, entretanto
não mudam sua temperatura consideravelmente. Isso acontece por dois motivos, pois o sistema
possui uma massa muito grande ou, pois o sistema possui um enorme calor específico.
Por exemplo: se jogarmos um cubo de gelo no mar e esperarmos, veremos que o gelo se
transformará em água e subirá de temperatura até entrar em equilíbrio térmico com o oceano.
Entretanto o oceano não mudou em nada sua temperatura, já que sua massa é absurdamente
grande, portanto podemos chamar o oceano de reservatório térmico.
Obs.:
Esse assunto não é muito cobrado de forma isolada em provas, geralmente utilizam-se das formulas
como (2) e (3) no meio de exercícios de entropia e de segunda lei da termodinâmica.
Colocaremos alguns exercícios no final do capítulo, mas eles consistem em encontrar a energia
gerada por alguma forma, seja por chama, por trabalho,..., e aplicar essa energia nas formulas (2) e
(3). Ou, então serão dados duas substancias uma que perde energia e outra que recebe essa mesma
energia perdida, dessa forma poderá igualar as equações de ambas, que irão compartilhar as
temperaturas finais (eq. térmico).
2 TRANSFERÊNCIA DE CALOR
Existem três formas de transferência de calor, por convecção, aplicável a fluidos; por
radiação, por meio de ondas eletromagnéticas; e por condução de calor, o que
estudaremos mais a fundo.
Você pode deduzir a formula da condução de calor se pensar no exemplo simples de
uma panela fervendo água, observe:
 O calor sempre flui do mais quente para o mais frio;
 É proporcional a -> se aumentar o fogo, a água ferve mais rápido;
 É inversamente proporcional à espessura da chapa ( ) -> quanto mais espesso
for o fundo da panela, mais demora a ferver a água;
 É proporcional a área (A) -> área do fundo da panela;
tempo
Juntando essas observações e considerando um infinitésimo de posição
temos que a variação de calor em relação é:
e de
(3)
Obs.: A constante “k” é chamada de condutividade térmica e é característica de cada material.
Materiais são bons condutores de calor quando possuem um alto valor de “k”, a
unidade do S.I. para a condutividade térmica é
.
Vamos então calcular a transferência de calor de dois reservatórios térmicos a
temperaturas
, unidos por uma barra de condutividade k.
Para facilitar, consideraremos um regime estacionário de transferência de calor, ou
seja, que não existem acúmulos de calor ao longo da barra, e que todo o calor transferido é
distribuído igualmente ao longo da barra.
Resumindo... Regime estacionário -->
Substituindo essa relação em (3), chegamos (note que o sinal de “–“ da fórmula vai cancelar com o
sinal de
):
(3.2)
Agora, vamos dificultar um pouco as coisas, utilizaremos duas barras em duas posições distintas,
mas ainda mantendo o regime estacionário, observe:
Primeiro modo
Segundo modo
Para calcular
no primeiro modo utilizaremos uma temperatura intermediaria
entre as duas barras, com isso teremos:
Por fim,
(3.3)
Para calcular o segundo caso, basta somar as duas transferências de calor,
relacionadas as duas barras, resultando em...
(3.4)
Exercícios Recomendados
[UFRJ-2014.1]
Resposta:
Bom, como os cilindros são idênticos, podemos escrever
formula 3.3, mas considerando as informações iguais e que
, tendo como base a
:
Agora usando (3.4):
Agora, basta comparar:
[UFRJ-Modificada]: Um engenheiro mecânico deseja estudar qual é a forma mais rápida de
transferir calor entre dois corpos. Para isso, ele dispõe de dois reservatórios térmicos a
temperaturas distintas
, duas barras de tamanhos
, de secção transversal
igual (ambas cilíndricas) e de capacidades térmicas
. Coloquem em ordem
crescente as taxas de transmissão de calor considerando os casos:
IReservatório 2-> Barra 1-> Reservatório 1.
IIReservatório 2 -> Barra 2-> Reservatório 1.
IIIReservatório2->Barra 1->Barra 2-> Teservatório 1.
Começando pelos casos mais fáceis, utilizamos a formula (3.2) para os casos I e II:
Agora, para resolver o caso III, precisaremos da formula (3.4):
Analisando as respostas:
Exercícios recomendados:
1) [Herch Moyses Nussenzveig]
Resposta: 13,1°C
2) [Herch Moyses Nussenzveig]
Resposta: 30.5g
3) [Herch Moyses Nussenzveig]
Resposta:
4) [ITA] Dois corpos feitos de chumbo estão suspensos a um mesmo ponto por fios de
comprimento iguais a 1,50 m . Esticam-se os dois fios ao longo de uma mesma horizontal e,
em seguida, abandonam-se os corpos, de forma que eles se chocam e ficam em repouso.
Desprezando as perdas mecânicas, admitindo que toda a energia se transforma em calor e
sabendo que o calor específico do chumbo é 0,130 J / g° C e a aceleração da gravidade é
9,80 m / s² , podemos afirmar que a elevação de temperatura dos corpos é :
5) [Saraeva] Uma lâmpada de aquecimento que gasta N = 54 watts, foi submersa em um
calorímetro transparente que contém 3 V = 650 cm de água. Em τ = 3min a água se aquece
em t = 3, 4º C . Que parte da energia Q , gasta pela lâmpada, é emitida ao exterior em forma
de energia radiante pelo calorímetro?
Gabarito:
1) 13,1°C 2)30,5g 3)
4)B 5) 5%
Bibliografia
- Contribuição das nossas anotações da aula do professor Marcos Brum (Instituto de Física).
- Nussenzveig, H. Moysés. Curso de Física Básica vol. 2 Fluidos, Oscilações e Ondas, Calor. 4ª Edição,
revista. Editora Buchler.