PÊNDULO SIMPLES 1. Objectivo 2. Introdução

Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
Mecânica A
2008/09
_______________________________________________________________________________________________
PÊNDULO SIMPLES
1.
Objectivo
Neste trabalho pretende-se:
2.
•
Comparar a precisão de diferentes processos de medida;
•
Linearizar uma expressão;
•
Determinar a aceleração da gravidade.
Introdução
O pêndulo simples é um sistema constituído por uma massa pontual m, suspensa de um
ponto por um fio inextensível e de massa desprezável quando comparada com m, e que oscila em
torno desse ponto. Durante a oscilação, a massa descreve uma trajectória circular cujo raio é o
comprimento l do pêndulo. O movimento não é uniforme porque nem o módulo nem a direcção e o
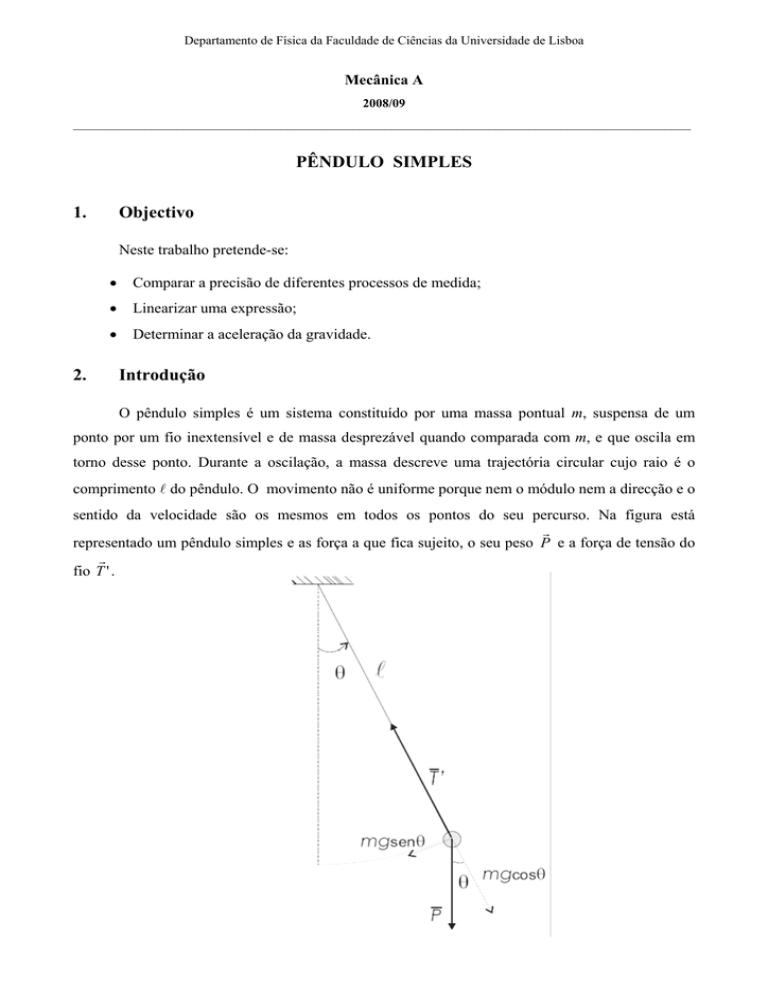
sentido da velocidade são os mesmos em todos os pontos do seu percurso. Na figura está
r
representado um pêndulo simples e as força a que fica sujeito, o seu peso P e a força de tensão do
r
fio T ' .
O pêndulo
A equação vectorial do movimento do corpo é
r r r
r
r r
P + T ' = FR = ma = m(at + a c )
(1)
r
r
r
r
onde FR é a força resultante e a a aceleração do movimento. at e a c são as componentes,
tangencial e centrípeta, da aceleração. Notamos que a componente tangencial do peso e,
r
consequentemente, a aceleração at está sempre dirigida no sentido do ponto de equilíbrio do
pêndulo, este é também o sentido da diminuição do ângulo θ, onde θ é o ângulo definido entre a
posição do pêndulo num dado instante e a direcção de equilíbrio do pêndulo.
Segundo as direcções normal e tangencial a equação (1) vem1:
T '− mgcosθ = mac
(1a)
− mg senθ = mat
(1b)
g é a aceleração da gravidade. A componente da aceleração segundo a direcção tangencial é obtida
da variação do módulo da velocidade com o tempo
 dθ 
 ds 
d  d l 
dv
d2θ
dt
dt 
at =
=l 2
=  = 
dt
dt
dt
dt
(2)
Da presença de uma força tangencial resulta a variação do módulo da velocidade do pêndulo. A
força central faz variar a direcção da velocidade mas não altera o seu módulo.
Substituindo em (1b) a expressão de at obtida em (2), vem:
d2θ
ml 2 = − mg senθ
dt
(3)
d2 θ g
+ senθ = 0
dt 2 l
(4)
d2 θ g
+ θ=0
dt 2 l
(5)
ou,
Para pequenos ângulos, senθ ≈ θ e vem:
1
No final do texto encontra-se em adenda este desenvolvimento mais detalhado
2(8)
O pêndulo
Uma solução desta equação é do tipo θ = θ0 sen(ωt + δ) onde δ e θ0 são obtidos das condições
iniciais; θ0 é a amplitude angular do movimento, δ a fase quando t = 0 e ω a frequência angular do
movimento. Substituindo em (5) vem:
− ω 2θ +
g
θ =0
l
(6)
donde,
ω=
g
l
(7)
Usando ω = 2π/T, sendo T o período do movimento, vem
T = 2π
l
g
(8)
Se não tivéssemos usado a aproximação dos pequenos ângulos, em vez de (8), teríamos obtido a
relação
T = 2π
3.

l 1
θ
1 + sen 2   + ...
g 4
2

(9)
Para resolver antes da aula de realização do trabalho
1) Parta das expressões (8) e (9). Despreze os termos de ordem superior a sen2(θ/2) e
determine o afastamento angular máximo que o pêndulo pode ter em relação à posição de
equilíbrio para que seja válida a expressão (8) com um erro inferior a: a) 0.1%; b) 1%.
2) Calcule o afastamento horizontal que corresponde ao afastamento angular máximo para
um erro inferior a 0.1% quando o comprimento do pêndulo é de 45 cm.
3) Se t10 = 10 T for medido com um erro ∆t10 qual é o erro ∆T associado a T?
 2π 


B
=
ln
4) Admita como conhecido o valor de
 g  e de ∆B. Determine g e ∆g.


3(8)
O pêndulo
4.
Realização experimental
Material: pêndulo, DataStudio, cronómetro, fita métrica, craveira.
4.1. Medição do período de um pêndulo. Precisão do processo de medida
Monte o pêndulo que lhe é fornecido, utilizando um comprimento de aproximadamente
45 cm. Coloque o sistema em oscilação, largando o corpo de uma posição correspondente a um
pequeno desvio angular. Tomaremos como medida de precisão o limite superior do erro,
calculado a partir dos maiores desvios em relação à média.
A – Utilização de um cronómetro comandado manualmente
1. Cada elemento do grupo determina o período de oscilação do pêndulo T a partir da medição
do tempo que o pêndulo leva a efectuar 10 oscilações completas, t10 + ∆t10. Não é necessário
voltar a colocar o pêndulo a oscilar quando muda o elemento do grupo de trabalho que faz as
medições.
2. Cada aluno repete a medição feita em 1. de modo que o grupo de trabalho obtenha 5 valores
do tempo de 10 oscilações completas.
3. Construa uma tabela com os 5 valores obtidos por todos os elementos do grupo para t10.
Obtenha o valor médio e o maior desvio relativamente à média.
4. Compare a incerteza resultante da dispersão de valores (maior desvio relativamente à média)
com a incerteza de cada medição associada à resolução experimental do cronómetro (erro de
leitura). Apresente o resultado na forma t10 + ∆t10 onde t10 é o valor médio das 5 medições e
∆t10 é o maior valor entre a incerteza resultante da dispersão de valores e a incerteza de cada
medição associada à resolução experimental do cronómetro.
5. Discuta as fontes de erro que neste caso conduzem à dispersão de resultados. Qual considera
ser a principal razão para a dispersão de valores obtidos?
6. Qual é a melhor estimativa de T + ∆T que conseguiu obter com este método manual?
B – Utilização de um cronómetro com sistema automático de aquisição
O sistema automático de registo do período, com aquisição pelo computador recorrendo
ao programa DataStudio, inclui um sensor óptico de passagem que deve ser colocado na posição
de equilíbrio do oscilador (opção sensor: fotoporta e pêndulo).
4(8)
O pêndulo
Sem alterar o comprimento do pêndulo, meça com a craveira o diâmetro da esfera
suspensa e registe o resultado na forma d + ∆d. Tal como na experiência anterior coloque o
sistema em oscilação, largando o corpo de uma posição correspondente a um pequeno desvio
angular.
Use o sistema automático de registo do período e, a partir do registo de 50 valores,
obtenha o período do pêndulo e a incerteza associada, T + ∆T. Para facilitar o seu trabalho
configure o programa de aquisição de forma a mostrar as seguintes estatísticas: valores médio,
mínimo e máximo, e nº de contagens.
Discuta qual dos dois processos de medida, manual ou automático, lhe permite ter mais
precisão na determinação do período.
Observação: Preste atenção aos dados registados no computador. Para além do registo do período o
sistema regista a velocidade do movimento do pêndulo na posição de equilíbrio do pêndulo. Como é
calculada? Use o Datastudio para visualizar os dados que acabou de adquirir. Como varia no tempo o
período do movimento? E a velocidade num dado ponto? Será este sistema conservativo? O que se passa
entretanto com a amplitude do movimento?
4.2. Determinação de g e linearização de uma expressão
Para comprimentos do pêndulo entre cerca de 30 cm e 120 cm, com intervalos de 15 cm,
efectue medições do período do pêndulo. Note que o comprimento do pêndulo é a distância entre
o ponto de suspensão e o centro de gravidade da massa suspensa.
1. Parta de um comprimento de fio próximo de 30 cm. Use a craveira para medir a altura da
massa suspensa e registe o resultado na forma h + ∆h. Meça com todo o cuidado o
comprimento do fio L + ∆L de modo a obter o comprimento l do pêndulo com a menor
incerteza possível. Registe o comprimento do pêndulo na forma l + ∆l.
2. Coloque o sistema em oscilação, largando o corpo de uma posição que verifique as
condições de validade da relação (8) com um erro inferior a 0.1%, e faça as medições do
período do pêndulo com o sistema automático de medida. Registe no caderno os valores
médio, mínimo e máximo do período em 10 oscilações e apresente o resultado na forma
T + ∆T, onde ∆T é o maior desvio em relação ao valor médio.
3.
Repita as operações 2. e 3. para os outros valores do comprimento do pêndulo.
5(8)
O pêndulo
4.
Represente graficamente T = f(l). Observe atentamente o comportamento da variação de T
com l. Note que a relação entre estas duas grandezas só numa observação descuidada pode ser tomada como
linear, ela apresenta um desvio sistemático a essa mesma linearidade.
5. Na relação (8) comece por associar os factores constantes e aplique logaritmos. Obtém uma
relação do tipo Y = AX + B. Identifique as variáveis X e Y e os parâmetros A e B.
6. Na tabela, tome os logaritmos de T e de l e, em seguida, faça a representação gráfica de
lnT = f(lnl). Compare a representação log-log com a representação em escala linear obtida
anteriormente. O que pode concluir desses resultados?
7.
Ajuste uma recta aos pontos experimentais lnT = f(lnl). Obtenha os parâmetros do ajuste e as
correspondentes incertezas. No Excel, ao adicionar a linha tendência com a equação no gráfico apenas
obtém os valores de A e B. Para obter o valor de ∆B deverá escolher o menu “Tools”, “Data analysis” e
“Regression”. Esta opção só aparece quando se selecciona os dois “Analysis Toolpak” no menu “Add-Ins”.
8.
A partir dos valores dos parâmetros ajustados determine a aceleração da gravidade, g + ∆g.
Compare o valor determinado com o valor adoptado para aceleração da gravidade padrão:
g = 9.80665 m/s². Qual terá sido a principal fonte de erro? Note que um pequeno afastamento entre
g medido e g tabelado indica grande rigor na determinação.
9. Compare também o valor do parâmetro A com o valor esperado de acordo com a
identificação feita em 6.
FORMULAS PARA A PROPAGAÇÃO DE ERROS
Limite superior do erro: dadas as quantidades A ± ∆A , B ± ∆B e uma constante α :
o se X = A + B ou X = A − B então ∆X = ∆A + ∆B
o se Y = α A então ∆Y = α ∆A
o se Z = A B ou Z =
A
∆Z ∆A ∆B
então
=
+
B
Z
A
B
6(8)
O pêndulo
Adenda
Obtenção das equações de movimento do pêndulo
r
Supomos o pêndulo simples representado na figura. r é o vector posição da massa m do pêndulo
r
r r
r
suspensa do ponto O e de comprimento r = r . u r é o vector unitário da direcção de r e u θ é o
r
vector unitário perpendicular a r e dirigido no sentido do crescimento de θ.
r
r
Os vectores unitários u r e u θ acompanham o pêndulo no seu movimento. Começamos por
r r
r
r
exprimir u r e u θ nos vectores unitários do eixo dos xx e dos yy, u x e u y , respectivamente.
r
r
r
π
r
π
r
u r = cos − θ  u x − sen − θ u y = senθ u x − cosθ u y
2

2

r
r
r
u θ = cosθ u x + senθ u y
(A1)
r
r r
Vamos exprimir o vector velocidade v nos vectores unitários u r e u θ .
r
r
r
r
du r
du r
r dr d(ru r ) dr r
v=
ur + r
=
=
=r
dt
dt
dt
dt
dt
(A2)
porque no pêndulo r é constante. De (A1) obtemos
r
du r
r
r dθ d θ r
= (cosθ u x + senθ u y )
=
uθ
dt
dt d t
(A3)
7(8)
O pêndulo
Substituindo (A3) em (A2) chegamos a
r
dθ r
v =r
uθ
dt
(A4)
Derivando, o vector velocidade agora obtido, em ordem ao tempo, encontramos o vector aceleração,
r
r
r dv
d2θ r
d θ du θ
a=
= r 2 uθ + r
dt
d t dt
dt
(A5)
Usando (A1) obtemos
r
du θ
r
r dθ
r  dθ 
= (− senθ u x + cosθ u y )
= −u r  
dt
dt
 dt 
(A6)
que substituímos em (A5) e vem
r
2
r
r r
r dv
d2θ r
 dθ 
a=
= r 2 u θ + r   (− u r ) = at + a c
dt
dt
 dt 
(A7)
Da equação vectorial (1)
r r r
r
r r
P + T ' = FR = ma = m(at + a c )
r
r
r
r
decompondo P e T ' segundo as direcções de u r e u θ e usando (A7), obtemos
2
r
r
r
 dθ  r
T ' (−u r ) + mgcosθ u r = − mr   u r = ma c
 dt 
r
r
d2 θ r
− mgsenθ u θ = mr 2 u θ = mat
dt
(A8)
r
r
Como esperávamos a componente centrípeta da aceleração a c tem sempre sentido contrário a u r
r
como se vê pela 1ª equação (A8). A componente tangencial da aceleração at tem sentido contrário
r
d2 θ
a u θ , isto é, aponta na direcção da posição de equilíbrio do pêndulo e 2 < 0 .
dt
Na forma escalar as equações (A8) vêm:
 dθ 
− T '+ mgcosθ = −mr  
 dt 
2
d θ
− mgsenθ = mr 2
dt
2
(A9)
Estas equações são as equações já apresentadas em (1a), (1b) e (2).
8(8)