LISTA 02 DE EXERCÍCIOS – GEOMETRIA PLANA – PROF

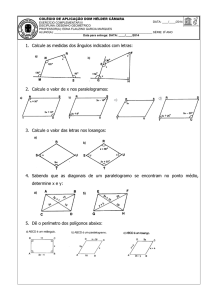
08. No retângulo da figura ao lado, tem-se que:
ABˆ D  x
ADˆ E  EDˆ B ,
BEˆ D  130 ,
ˆ
e DBC  y . Calcule x e y.
LISTA 02 DE EXERCÍCIOS – GEOMETRIA PLANA – PROF. ROGERINHO
D
A
1º Ensino Médio
(Tangência, ângulos na circunf., quadriláteros, pontos notáveis do , teorema de Tales e semelhança de a)
C
E
B
Nome:__________________________________________ n° _______ turma _________
09. Sabendo que os ângulos obtusos de um losango são expressos por x  80º e
2 x  20º , calcule as medidas dos quatro ângulos desse losango.
01. Se ABCD é um trapézio de bases AB e CD , determine x e y.
a)
b)
D
C
D
C
10. A diagonal de um losango forma com um de seus lados um ângulo de 55°. Determine
os quatro ângulos do losango.
x+20°
x
A
y
y
y–30°
x
x–15°
A
B
11. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
a)
b)
x–y
B
02. Num trapézio retângulo, a medida do maior ângulo interno é o quádruplo da medida
do menor. Calcule as medidas desses dois ângulos.
03. Se ABCD é um paralelogramo,
Cˆ  x  70 , determine B̂ .
Aˆ  2 x
A
e
D
B
C
5
04. A soma de dois ângulos opostos de um paralelogramo é igual a
da soma das
13
medidas dos outros dois ângulos opostos. Determine as medidas dos quatro ângulos.
12. Dada a figura e sendo BD  4 , AF  3 e EC  5 ,
onde os pontos D, E e F são pontos de tangência,
calcule o perímetro do triângulo ABC.
A
B
2
05. Num paralelogramo, a medida de um lado é
da medida do outro. Sabendo que seu
3
perímetro é 120cm , calcule o comprimento de cada lado.
13. Calcule o valor de x na figura ao lado:
20
12
06. Calcule os ângulos de um paralelogramo sabendo que uma de suas diagonais forma
com os lados ângulos de 42° e 78°.
07. Sendo ABCD um paralelogramo, AP é bissetriz,
AB  7cm e PC  3cm , determine o perímetro
do paralelogramo.
B
A
P
C
D
x
16
14. Na figura, o quadrilátero ABCD está circunscrito
na circunferência de centro O. Sendo
AB  (2 x  1)cm , BC  10cm , CD  (3x  2)cm
e AD  8cm , calcule a medida do lado AB .
F
D
E
C
15. Calcule o perímetro de um quadrilátero ABCD circunscrito a uma circunferência,
sabendo que três de seus lados medem AB  5cm , BC  3cm e AD  4,5cm .
21. Qual é a medida do ângulo CDˆ A inscrito na circunferência de centro O?
16. Determine a medida do diâmetro da circunferência inscrita em um triângulo
retângulo cujos lados medem 15m, 20m e 25m.
17. Determine a medida de um dos lados não paralelos de um trapézio isósceles,
circunscrito a um círculo, sabendo que as suas bases medem 60m e 20m.
18. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
a)
b)
c)
22. Na circunferência de centro O, o arco AD
y
mede 120°, ADˆ O  y , BAˆ C  x e ACˆ B  .
2
Calcule x e y.
120°
D
A
C
O
B
19. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
a)
b)
23. Na circunferência de centro O, o arco menor
AB mede 100º. Calcule a medida do ângulo 
20. Na figura, AB é o diâmetro da circunferência de centro
O, e o arco ABC  238º . Calcule a medida do ângulo
BAˆ C .
24. Na circunferência de centro O, calcule os
ângulos CBˆ A  x e CDˆ A  y , que estão
inscritos na circunferência.
25. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
a ) ABˆ C  130º
b ) ADˆ C  138º
c ) Dado BAD  310º
28. Em cada uma das circunferências de centro O a seguir, calcule o valor de x.
a ) Dados AMB  106º e
b ) Dados AEˆ B  42º e CND  58º
( AMB  x )
CND  34º
29. Em cada uma das figuras, o centro da circunferência é o ponto O. Sendo B e C
pontos de tangência, calcule o valor de x.
a ) Dado BMC  240
b)
26. (MACK) O quadrilátero ABCD da figura é
inscritível. Determine o valor de x.
27. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
a ) Dados AMB  42º e
b ) Dados AMB  132º e AEˆ B  90º
CND  108º ( AEˆ D  x )
( CND  x )
30. Na figura, determine a medida do ângulo ,
sabendo que o arco AB mede 100° e que a corda
CD mede r, sendo r a medida do raio do círculo.
C
D

A
31. Na figura, a reta BC passa pelo
centro O da circunferência e
intercepta a reta DE no ponto A,
BCD  235º
DOˆ E  100º .
e
Calcule a medida do ângulo CAˆ D .
B
32. Calcule x e y nas figuras abaixo:
c) AB  AC , BAˆ C  x ,
BDˆ A  y , DAˆ C  35
b) BEˆ D  40 ,
a) AE  x , BD  y ,
e ACˆ E  25
ADˆ C  120 e
ACˆ E  x
APˆ E  80
e ABˆ D  DBˆ C
A
A
B
C
A
B
P
C
D
D
B
E
C
A
y
N
41. Num triângulo isósceles, um ângulo  mede 100°. Qual a medida do ângulo agudo
formado pelas alturas que não passam pelo
vértice A?
x
y+2
7-x
B
M
C
34. Sendo o triângulo ABC retângulo em A e M o ponto médio de BC , calcule x e y.
a)
b)
C
A
3x
M
y
20º
B
c)
M
C
d)
A
42. O triângulo ABC é retângulo em A; AD é
mediana e CE é a bissetriz interna. Se o ângulo
ABˆ C  40 , calcule a medida do ângulo CFˆD
formado pela mediana AD com a bissetriz CE .
43. Dada a figura, sabendo que AC  60 , determine PB.
3
A
C
60°
y
12
x
38. Em um triângulo ABC, os ângulos A e B medem, respectivamente, 76° e 34°.
Determine o ângulo agudo formado pela mediatriz do lado BC com a bissetriz do
ângulo C.
40. A hipotenusa de um triângulo mede 20cm e um dos ângulos mede 20°.
a) Qual a medida da mediana relativa à hipotenusa?
b) Qual a medida do ângulo formado por essa mediana e pela bissetriz do ângulo
reto?
E
33. Na figura os segmentos com
“marcas iguais” são congruentes.
Determine os valores de x e y.
medida do ângulo  .
39. Em um triângulo ABC, os ângulos B e C medem, respectivamente, 74° e 32°. Se I é o
incentro e O é o ortocentro, calcule a medida do ângulo IAˆ O .
P
D
37. Sendo H o ortocentro de um triângulo acutângulo ABC e BHˆ C  150 , determine a
C
B
M
P
C
S
A
y
M
N
B
M
y
x
x
A
B
20°
A
B
AS é bissetriz
35. Se P é o incentro de um triângulo ABC e BPˆ C  125 , determine  .
36. Se H é o ortocentro de um triângulo isósceles ABC de base BC e BHˆ C  130 ,
determine os ângulos desse triângulo.
44. (MACK) Na figura, sendo
determine o valor de x.
a // b // c ,
E
B
F
D
C
45. Três terrenos têm frentes para a rua “A” e
para a rua “B”, conforme a figura. As
divisas laterais são perpendiculares à rua
“A”. Qual a medida de frente para a rua
“B” de cada lote, sabendo-se que a frente
total para essa rua é 120m?
50. Na figura, DE é paralelo a BC e AM é bissetriz interna. Calcule x e y.
Rua A
40
A
30
x
20
6
E
D
Rua B
5
2
B
M
4
C
y
46. Na figura, r // s // t . Calcule o valor de x.
51. Os três lados de um triângulo medem, respectivamente, 7m, 8m e 12m. Calcule a
medida do maior segmento que a bissetriz interna do triângulo determina sobre o
maior lado.
r
x–3
x
s
x+2
x–2
t
47. Se AB // DE , calcule x.
D
A
D
C
53. Na figura, se ABˆ C  AEˆ D , AD  8cm , DB  2cm e
AE  5cm , calcule a medida do segmento EC .
x
B
B
52. Na figura ao lado, as retas AB e CD são
paralelas. Sabendo-se que AB  136cm ,
CE  75cm e CD  50cm . Calcule a
medida do segmento AE .
A
E
1
3,5
E
D
C
2
E
B
A
48. Sendo    , calcular x.
54. (MACK) Na figura abaixo,
determine o valor de x.
5
3x+5

x+4

3

49. Na figura, CD é bissetriz interna do ângulo
de vértice C. Se AD  12cm , BD  20cm ,
AC  x e BC  2x  5 , calcule a medida do
C
x
55. Na figura abaixo, tem-se: AE  1cm ,
BC  3cm e CD  7cm . Determine a
medida de BE .
2x–5
lado BC .
A
12
D
20
B
C
56. Calcule o valor de x em cada uma das figuras.
a)
b)
A
61. Um triângulo cujos lados medem 24cm, 36cm e 40cm é semelhante a outro triângulo
de 30cm de perímetro. Calcule a medida do menor lado do segundo triângulo.
C
15
8
D
20

62. Determine o valor de x no trapézio ABCD da figura.
x
A

B
E
17
5
A
C
D
57. Determine x e y em cada caso:
a)

x
B
4
C
b)
4

y
y

5


x
x
24cm
63. Num retângulo ABCD, os lados AB e BC
medem 20cm e 12cm, respectivamente.
Sabendo-se que M é o ponto médio do lado
AB , calcular EF , distância do ponto E ao
lado AB , sendo E a intersecção da
diagonal BD com o segmento CM .
6
5
4
B
30cm
x

16cm
58. (FUVEST) Na figura, o triângulo ABC é
retângulo em A, ADEF é um quadrado,
AB  1 e AC  3 . Quanto mede o lado do
quadrado?
D
D
C
E
A
M
F
B
64. Na figura, o triângulo é isósceles e as circunferências têm raios 3m e 4m. Calcule a
altura h do triângulo.
h
59. A figura mostra um quadrado inscrito
num triângulo de base 20cm e altura
12cm. Calcule a medida do lado desse
quadrado.
65. O sol incide sobre uma pessoa de 1,60m de altura e sua sombra projetada sobre um
piso horizontal é de 2,40m.
Um poste vertical, situado no mesmo lugar, é projetado sobre o mesmo piso.
Algumas horas mais tarde, a sombra da pessoa, no mesmo piso e lugar é de 2,00m,
enquanto que o a sombra do poste recuou 2,50m. Calcule a altura do poste.
12cm
20cm
60. Os triângulos ABC e CDE da figura são
retângulos em B e em E. O segmento CD é
A
perpendicular a BC . Se AB  12cm ,
BC  16cm e DE  4cm , calcule a medida de
D
CE .
E
B
C
GABARITO
01. a) x  80; y  105
b) x  125; y  70
19. a) 35º
b) 70º
36. 65°, 65°, 50°
54. 11,25
37. 30°
55. 5cm
21. 125º
03. 40°
22. x  75º e y  30º
38. 55°
04. 50°; 130°; 50°; 130°
23. 40º
05. 24cm e 36cm
24. x  105º ; y  75º
25. a) 50°
b) 69°
07. 34cm
40. a) 10cm
09. 40º; 140°; 40°; 140°
10. 70°; 110°; 70°; 110°
b) 6
13. 4
14. 7cm
43. PB  20
59.
28. a) 36º
b) 142º
44. x  2
60. 3cm
29. a) 60º
b) 55º
45.
160
80
m, 40m,
m
3
3
31. 15º
46. 6
32. a) x  105; y  55
b) x  20
c) x  40; y  70
47. 7
48.
5
4
49. 25cm
b) 25º
c) 65º
15
cm ou 7,5cm
2
b) 48º
33. x  4; y  6
17. 40m
34. a)
b)
c)
d)
10
3
41. 80°
27. a) 75º
15. 19cm
16. 10m
57. a) 6 x ; y 
b) 96
42. 75°
30. 80°
12. 24
c) 25º
b) 25º
8
3
58. 0,75
26. 52º
08. x  10 e y  80
56. a)
39. 21°
06. 60°; 120°; 60°; 120°
18. a) 30º
52. 204cm
53. 11cm
20. 29º
02. 36° e 144°
11. a) 5
35. 70°
x  40; y  20
x  4; y  36
x  30; y  15
x  50; y  70
50. x  15; y  10
51. 6,4
61. 7,2cm
62. 12cm
63. 4cm
64. 32m
65. 10m
b) x 
15
;y5
2