1. (Espcex (Aman) 2014) Uma esfera é lançada com velocidade

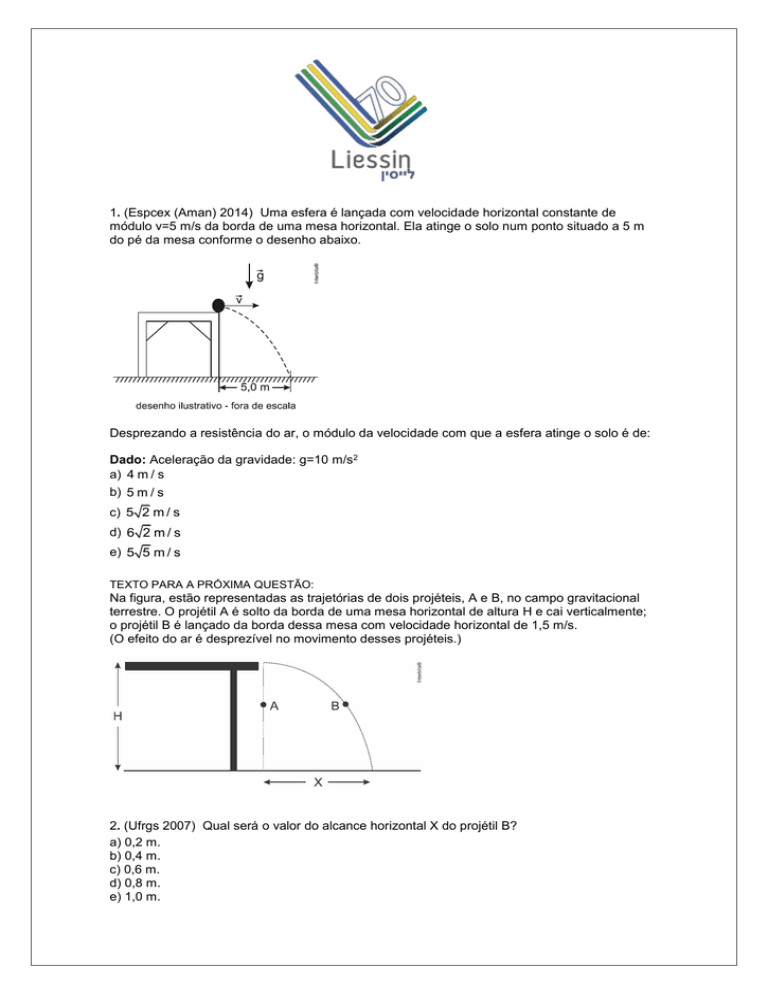
1. (Espcex (Aman) 2014) Uma esfera é lançada com velocidade horizontal constante de
módulo v=5 m/s da borda de uma mesa horizontal. Ela atinge o solo num ponto situado a 5 m
do pé da mesa conforme o desenho abaixo.
Desprezando a resistência do ar, o módulo da velocidade com que a esfera atinge o solo é de:
Dado: Aceleração da gravidade: g=10 m/s2
a) 4 m / s
b) 5 m / s
c) 5 2 m / s
d) 6 2 m / s
e) 5 5 m / s
TEXTO PARA A PRÓXIMA QUESTÃO:
Na figura, estão representadas as trajetórias de dois projéteis, A e B, no campo gravitacional
terrestre. O projétil A é solto da borda de uma mesa horizontal de altura H e cai verticalmente;
o projétil B é lançado da borda dessa mesa com velocidade horizontal de 1,5 m/s.
(O efeito do ar é desprezível no movimento desses projéteis.)
2. (Ufrgs 2007) Qual será o valor do alcance horizontal X do projétil B?
a) 0,2 m.
b) 0,4 m.
c) 0,6 m.
d) 0,8 m.
e) 1,0 m.
3. (Uft 2010) Um jogador de futebol chuta uma bola com massa igual a meio quilograma,
dando a ela uma velocidade inicial que faz um ângulo de 30 graus com a horizontal.
Desprezando a resistência do ar, qual o valor que melhor representa o módulo da velocidade
inicial da bola para que ela atinja uma altura máxima de 5 metros em relação ao ponto que
saiu?
Considere que o módulo da aceleração da gravidade vale 10 metros por segundo ao quadrado.
a) 10,5 m/s
b) 15,2 m/s
c) 32,0 m/s
d) 12,5 m/s
e) 20,0 m/s
4. (Fuvest 2011) Uma menina, segurando uma bola de tênis, corre com velocidade constante,
de módulo igual a 10,8 km/h, em trajetória retilínea, numa quadra plana e horizontal.
Num certo instante, a menina, com o braço esticado horizontalmente ao lado do corpo, sem
alterar o seu estado de movimento, solta a bola, que leva 0,5 s para atingir o solo. As
distâncias sm e sb percorridas, respectivamente, pela menina e pela bola, na direção horizontal,
entre o instante em que a menina soltou a bola (t = 0 s) e o instante t = 0,5 s, valem:
NOTE E ADOTE
Desconsiderar efeitos dissipativos.
a) sm = 1,25 m e sb = 0 m.
b) sm = 1,25 m e sb = 1,50 m.
c) sm = 1,50 m e sb = 0 m.
d) sm = 1,50 m e sb = 1,25 m.
e) sm = 1,50 m e sb = 1,50 m.
5. (G1 - ifce 2011) Numa pista circular de diâmetro 200 m, duas pessoas se deslocam no
mesmo sentido, partindo de pontos diametralmente opostos da pista. A primeira pessoa parte
com velocidade angular constante de 0,010 rad/s, e a segunda parte, simultaneamente, com
velocidade escalar constante de 0,8 m/s.
As duas pessoas estarão emparelhadas após (use π com duas casas decimais)
a) 18 minutos e 50 segundos.
b) 19 minutos e 10 segundos.
c) 20 minutos e 5 segundos.
d) 25 minutos e 50 segundos.
e) 26 minutos e 10 segundos.
6. (Ufrgs 2011) Um satélite geoestacionário está em órbita circular com raio de
aproximadamente 42.000 km em relação ao centro da Terra. Sobre esta situação, são feitas as
seguintes afirmações.
(Considere o período de rotação da Terra em torno de seu próprio eixo igual a 24h.)
Sobre esta situação, são feitas as seguintes afirmações.
I. O período de revolução do satélite é de 24h.
II. O trabalho realizado pela Terra sobre o satélite é nulo.
III. O módulo da velocidade do satélite é constante e vale 3500ð km/h.
Quais estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas I e III.
d) Apenas II e III.
e) I, II e III.
Gabarito:
Resposta da questão 1:
[E]
1ª Solução:
O tempo de queda da esfera é igual ao tempo para ela avançar 5 m com velocidade horizontal
constante de v0 = 5 m/s.
x
5
t
  1 s.
v0 5
A componente vertical da velocidade é:
v y  v0y  g t  v y  0  10 1  v y  10 m/s.
Compondo as velocidades horizontal e vertical no ponto de chegada:
v 2  v 02  v 2y  v  52  102
 v  125 
v  5 5 m/s.
2ª Solução:
Calculando a altura de queda:
1
2
h  g t 2  h  5 1
 h  5 m.
2
Pela conservação da energia mecânica:
m v02
m v2
m g h
2
2
v  5 5 m/s.
 v  v 02  2 g h  v  52  2 10 5   125 
Resposta da questão 2:
[C]
Como a componente horizontal da velocidade se mantém constante e o tempo de queda é o
mesmo para dos dois projéteis, temos:
x  vx t  1,5  0,4 
x  0,6 m.
Resposta da questão 3:
[E]
y
v0
v 0y
v = v 0x
5m
30°
v 0x
Aplicando Torricelli para o eixo y:
2
v2y  v0y
 2 g y .

v  v 0x  v y  0
No ponto mais alto: 

y  h
Substituindo:
x
2
02 = v0y
 2 g h  v0y =
2 g h  2(10)(5) = 10 m/s.
Mas:
v0y = v0 sen 30°  10 = v0
1
 v0 = 20 m/s.
2
Resposta da questão 4:
[E]
Dados: vx = 10,8 km/h = 3 m/s, tqueda = 0,5 s.
Durante a queda, a velocidade horizontal da bola é igual à velocidade da menina. Portanto:
sm = sb = vx tqueda = 3 (0,5) = 1,5 m.
Resposta da questão 5:
[E]
Dados: D = 200 m  r = 100 m; 2  0,01 rad/s;   3,14 .
A velocidade da pessoa mais rápida é:
v 2  2r  0,01 100  1 m / s.
Como partem de pontos diametralmente opostos, a distância (d) entre eles é meia volta.
d   r  3,14  100  314 m.
A pessoa mais rápida leva vantagem (velocidade relativa  vrel ) de 0,2 m/s.
O tempo para tirar essa diferença é:
t 
d
314

 1570 s
vrel 0,2

t  26 min e 10 s.
Resposta da questão 6:
[E]
I. Correto: para ser geoestacionário tem que ter período igual ao da Terra, isto é, 24hs.
II. Correto: a força de atração é perpendicular à velocidade em todo o movimento.
III. Correto:
2πr 2πx42.000
V

 3.500π km / h .
T
24