Múltiplos, Potências, Linhas e Pares de Ângulos

FICHA DE AVALIAÇÃO DE MATEMÁTICA
5.º ANO
Nome: _______________________________________________________________
Olá, Matemática! – 5.º Ano
ANO LETIVO 2013-2014
Ano / Turma: ______
N.º: _____
Data: ___ - ____ - ___
Avaliação
O Professor
Enc. de Educação
______________________
_____________________
______________________
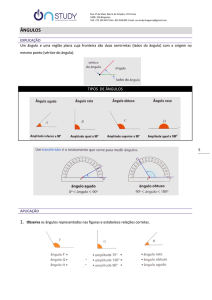
1. Com os algarismos 6 , 3 e 0 forma um número que seja:
1.1. ímpar;
1.2. múltiplo de 2 e de 5 ;
1.3. divisível simultaneamente por 3 e 4 .
2. No dia do seu aniversário, a Maria pretende oferecer a cada um dos seus 25 amigos
um saquinho com rebuçados e gomas. Se ela colocar em cada saquinho 5 rebuçados
e 3 gomas, quantas guloseimas ela vai precisar?
3. Calcula o valor das seguintes expressões numéricas.
3.1. (4 − 1) × 2 =
3.2. 4 × 6 − 2 × 2 =
3.3. 2 + 3 × 5 − 42 =
3.4. 5 × 2 − (32 − 2) =
3.5. 6 − 2 × ( 1 + 8 ∶ 2 ) ∶ 5 − ( 3 − 2 ) =
4.
Usando o algoritmo de Euclides:
4.1. simplifica a fração
30
84
.
4.2. calcula os divisores comuns dos números 30 e 84 .
Página 1 de 5
[email protected]
Ficha de Avaliação de Matemática - 5.o ano
Ano letivo 2013/2014
5. Um padeiro produz vários tipos de pão. Para rentabilizar a produção utiliza dois
fornos simultaneamente, durante todo o dia.
5.1. Num dos fornos coloca a cozer pão de centeio, de vinte
em vinte minutos, e no outro forno pão de trigo de
quinze em quinze minutos. Ao meio-dia, de hoje, o
padeiro colocou a cozer simultaneamente os dois tipos
de pão: passados quantos minutos voltará a acontecer
esta mesma situação?
5.2. Numa fornada o padeiro obteve 200 pães de centeio e 180 pães de trigo.
5.2.1. Qual o número máximo de clientes a que poderá fornecer estes dois tipos
de pão se tiver de vender exatamente a mesma quantidade de pães de
centeio e de trigo a cada cliente?
5.2.2. Quantos pães de centeio e de trigo venderá o padeiro a cada cliente?
6.
Considera a figura ao lado onde AB é paralela a CD .
Indica:
6.1. um ângulo reto;
6.2. um ângulo agudo;
6.3. um ângulo obtuso;
6.4. um segmento de reta;
6.5. uma reta perpendicular a AB ;
6.6. uma semirreta diretamente paralela a 𝐴̇𝐵 ;
6.7. uma semirreta inversamente paralela a 𝐴̇𝐵 .
Página 2 de 5
[email protected]
Ficha de Avaliação de Matemática - 5.o ano
7.
Faz corresponder as colunas A e B considerando as seguintes figuras.
COLUNA A
Ângulo giro 
Retas estritamente paralelas

Ângulos verticalmente opostos

Ângulo raso 
Ângulos complementares 
Retas concorrentes oblíquas 
Ângulos adjacentes 
8.
Ano letivo 2013/2014
COLUNA B
 Figura 1
 Figura 2
 Figura 3




Figura 4
Figura 5
Figura 6
Figura 7
Considera os ângulos 𝑎 e 𝑏 apresentados de seguida.
𝑏
𝑎
8.1.
Utilizando compasso e régua:
8.1.1. traça a bissetriz do ângulo 𝑎 ;
8.1.2. constrói o ângulo que é a soma de 𝑎 e 𝑏 .
8.2.
Utilizando um transferidor determina a amplitude do ângulo 𝑏 .
Página 3 de 5
[email protected]
Ficha de Avaliação de Matemática - 5.o ano
9.
Ano letivo 2013/2014
Considera a figura ao lado que representa duas retas r e s intersetadas por uma
secante t .
𝑡
9.1.
𝑏
Indica um par de ângulos:
9.1.1. alternos internos;
𝑐
𝑎
𝑟
𝑑
9.1.2. correspondentes;
𝑓
9.1.3. alternos externos;
𝑒
𝑠
𝑔
ℎ
9.1.4. suplementares.
Sendo 𝑎̂ = 40° , indica, justificando, qual a amplitude do ângulo:
9.2.
9.2.1. 𝑐
9.2.2. 𝑑
10. Completa os espaços em branco, apresentando todos os cálculos.
10.1.
30o = _____ '
10.2.
3500'' = _____ ' _____ ''
10.3.
5000'' = _____ o _____ ' _____ ''
11. Para cada uma das alíneas, determina a amplitude dos ângulos 𝑥 , 𝑦 e 𝑧 ,
justificando a tua resposta.
11.1.
Página 4 de 5
[email protected]
Ficha de Avaliação de Matemática - 5.o ano
Ano letivo 2013/2014
11.2.
11.3.
11.4.
11.5.
Página 5 de 5
[email protected]
PROPOSTA DE RESOLUÇÃO
Olá, Matemática! – 5.º Ano
5.º ANO
FICHA DE AVALIAÇÃO DE MATEMÁTICA
ANO LETIVO 2013-2014
1.
1.1. 603
1.2. 630 ou 360
1.3. 360
2. Rebuçados: 5
Gomas: 3
Número total de guloseimas:
25 × (5 + 3) = 25 × 8 = 200
A Maria vai precisar de 200 guloseimas.
3.
3.1. (4 − 1) × 2 =
=3×2=
=6
3.2. 4 × 6 − 2 × 2 =
= 24 − 4 =
= 20
3.3. 2 + 3 × 5 − 42 =
= 2 + 15 − 16 =
= 17 − 16 =
=1
3.4. 5 × 2 − (32 − 2) =
= 10 − (9 − 2) =
= 10 − 7 =
=3
3.5. 6 − 2 × ( 1 + 8 ∶ 2 ) ∶ 5 − ( 3 − 2 ) =
= 6 − 2 × (1 + 4) ∶ 5 − 1 =
=6−2×5∶ 5−1=
= 6 − 10 ∶ 5 − 1 =
=6−2−1 =
=4−1=
=3
Página 1 de 4
[email protected]
Proposta de resolução da Ficha de Avaliação de Matemática - 5.o ano
Ano letivo 2013/2014
4.
4.1.
84 30
24 2
30 24
6 1
24 6
0 4
m.d.c. (30 , 84) = 6
Dividindo cada um dos termos da fração pelo m.d.c. (30 , 84) , obtemos uma
fração irredutível equivalente à dada:
30
84
5
= 14 .
4.2. Os divisores comuns de 30 e 84 são os divisores de 6 , isto é, 1 , 2 , 3 e 6 .
5.
5.1.
M20 = {0 , 20 , 40 , 60 , ...}
M15 = {0 , 15 , 30 , 45 , 60 , ...}
O menor múltiplo comum entre 20 e 15 é 60 .
O padeiro voltará a colocar os dois tipos de pão no forno em simultâneo ao fim de
60 minutos.
5.2.
5.2.1.
200 180
20 1
180 20
0 9
m.d.c. (200 , 180) = 20
Vinte é o número máximo de clientes a que o padeiro poderá fornecer
estes dois tipos de pão se tiver de vender exatamente a mesma quantidade
de pão de centeio e de trigo a cada um.
5.2.2. Pão de centeio - 200 : 20 = 10
Pão de trigo 180 : 20 = 9
O padeiro venderá a cada cliente 10 pães de centeio e 9 pães de trigo.
Página 2 de 4
[email protected]
Proposta de resolução da Ficha de Avaliação de Matemática - 5.o ano
Ano letivo 2013/2014
6.
6.1. Ângulos BAE ou CAB
6.2. Por exemplo: ângulos EBA , ABC , DCB .
6.3. Ângulos DAE ou EBD
6.4. Por exemplo: [BD]
6.5. AC (também designável por AE ou CE)
6.6. 𝐶̇ 𝐷
6.7. 𝐷̇ 𝐶
7.
COLUNA A
Ângulo giro 
Retas estritamente paralelas

Ângulos verticalmente opostos

Ângulo raso 
Ângulos complementares 
Retas concorrentes oblíquas 
Ângulos adjacentes 
COLUNA B
 Figura 1
 Figura 2
 Figura 3




Figura 4
Figura 5
Figura 6
Figura 7
8.
8.1.
8.1.1.
8.1.2.
8.2.
𝑏̂ = 70°
Página 3 de 4
[email protected]
Proposta de resolução da Ficha de Avaliação de Matemática - 5.o ano
Ano letivo 2013/2014
9.
9.1.
9.1.1. Ângulos 𝑐 e 𝑒 ; ângulos 𝑑 e 𝑓 .
9.1.2. Ângulos 𝑎 e 𝑒 ; ângulos 𝑏 e 𝑓 ; ângulos 𝑐 e 𝑔 ; ângulos 𝑑 e ℎ .
9.1.3. Ângulos 𝑎 e 𝑔 ; ângulos 𝑏 e ℎ .
9.1.4. Por exemplo: ângulos 𝑎 e 𝑏 .
9.2.
9.2.1. 𝑐̂ = 40° porque os ângulos 𝑎 e 𝑐 são verticalmente opostos, logo são
geometricamente iguais.
9.2.2. 𝑑̂ = 140° porque os ângulos 𝑎 e 𝑑 são suplementares, logo a soma das
suas amplitudes é 180o .
10.
10.1.
30o = 1800 '
10.2.
3500'' = 58 ' 20 ''
10.3.
5000'' = 1 o 23 ' 20 ''
11. Por exemplo:
̂ = 90° − 25° = 65°
11.1. 𝑥
amplitude de
25o
.
11.2. ̂
𝑥 = 180° − 33° = 147°
amplitude de
33o
porque é ângulo complementar de um ângulo com
porque é ângulo suplementar de um ângulo com
.
̂ = 147° porque é ângulo correspondente do ângulo 𝑥 em relação a uma
𝑦
secante de duas retas paralelas .
̂ = 36° porque r é bissetriz do ângulo NOP e divide este ângulo em dois
11.3. 𝑦
ângulos geometricamente iguais.
̂ = 113° porque é um ângulo de lados paralelos dois a dois com um ângulo de
11.4. 𝑥
amplitude 113o da mesma espécie (ambos obtusos).
̂ = 180° − 113° = 67° porque é um ângulo de lados paralelos dois a dois com
𝑦
um ângulo de amplitude 113o de espécie diferente (um agudo e o outro obtuso).
̂ = 34° porque é um ângulo de lados perpendiculares dois a dois com o ângulo
11.5. 𝑦
CDB de amplitude 34o e são ângulos da mesma espécie (ambos agudos).
Página 4 de 4
[email protected]