Lista de Exercícios – Trigonometria e Triângulo Retângulo 1(Cefet

Lista de Exercícios – Trigonometria e Triângulo
Retângulo
1(Cefet – PR) A rua Tenório Quadros e a avenida Teófilo
Silva, ambas retilíneas, cruzam-se conforme um ângulo
de 30º. O posto de gasolina Estrela do Sul encontra-se
na avenida Teófilo Silva a 4 000 m do citado cruzamento.
Portanto, determine em quilômetros, a distância entre o
posto de gasolina Estrela do Sul e a rua Tenório
Quadros?(R:2,3km)
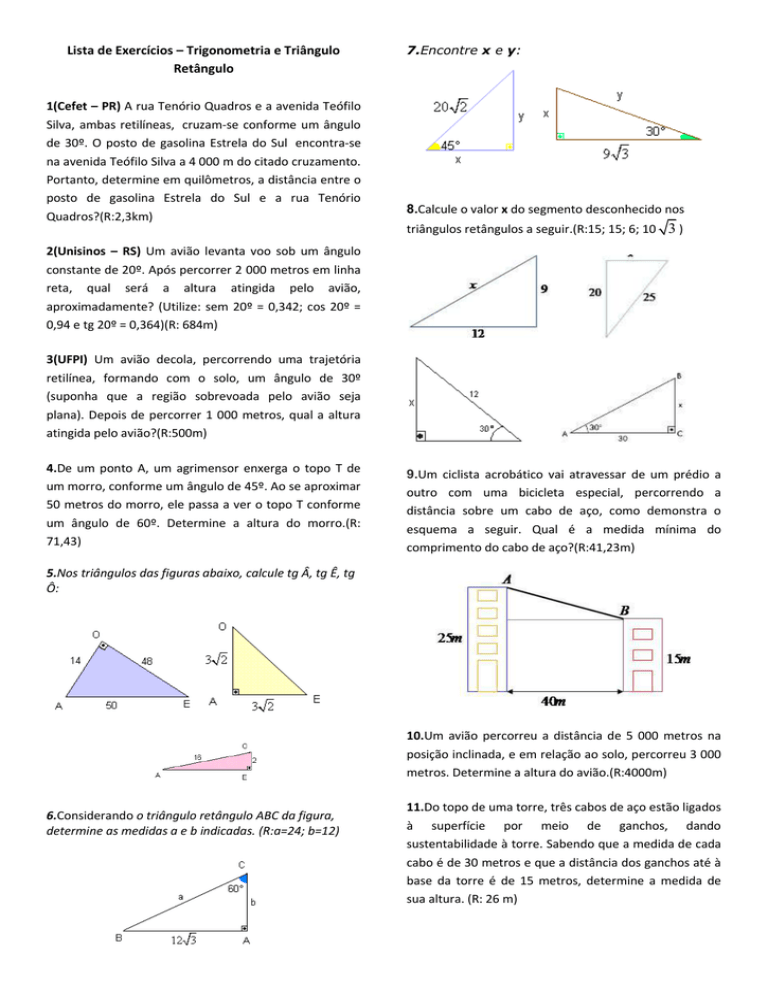
7.Encontre x e y:
8.Calcule o valor x do segmento desconhecido nos
triângulos retângulos a seguir.(R:15; 15; 6; 10 3 )
2(Unisinos – RS) Um avião levanta voo sob um ângulo
constante de 20º. Após percorrer 2 000 metros em linha
reta, qual será a altura atingida pelo avião,
aproximadamente? (Utilize: sem 20º = 0,342; cos 20º =
0,94 e tg 20º = 0,364)(R: 684m)
3(UFPI) Um avião decola, percorrendo uma trajetória
retilínea, formando com o solo, um ângulo de 30º
(suponha que a região sobrevoada pelo avião seja
plana). Depois de percorrer 1 000 metros, qual a altura
atingida pelo avião?(R:500m)
4.De um ponto A, um agrimensor enxerga o topo T de
um morro, conforme um ângulo de 45º. Ao se aproximar
50 metros do morro, ele passa a ver o topo T conforme
um ângulo de 60º. Determine a altura do morro.(R:
71,43)
9.Um ciclista acrobático vai atravessar de um prédio a
outro com uma bicicleta especial, percorrendo a
distância sobre um cabo de aço, como demonstra o
esquema a seguir. Qual é a medida mínima do
comprimento do cabo de aço?(R:41,23m)
5.Nos triângulos das figuras abaixo, calcule tg Â, tg Ê, tg
Ô:
10.Um avião percorreu a distância de 5 000 metros na
posição inclinada, e em relação ao solo, percorreu 3 000
metros. Determine a altura do avião.(R:4000m)
6.Considerando o triângulo retângulo ABC da figura,
determine as medidas a e b indicadas. (R:a=24; b=12)
11.Do topo de uma torre, três cabos de aço estão ligados
à superfície por meio de ganchos, dando
sustentabilidade à torre. Sabendo que a medida de cada
cabo é de 30 metros e que a distância dos ganchos até à
base da torre é de 15 metros, determine a medida de
sua altura. (R: 26 m)
12.Uma escada de 12 metros de comprimento está
apoiada sob um muro. A base da escada está distante do
muro cerca de 8 metros. Determine a altura do
muro.Use
13.Calcule a metragem de arame utilizado para cercar
um terreno triangular com as medidas perpendiculares
de 60 e 80 metros, considerando que a cerca de arame
terá 4 fios. (R: 960 m)
14.Na cidade de pisa, Itália, está localizada a Torre de
Pisa, um dos monumentos mais famosos do mundo.
Atualmente, a torre faz, na sua inclinação, um ângulo de
74º com o solo. Quando o sol está bem em cima da torre
(a pino) ela projeta uma sombra de 15 m de
comprimento. A que distância se encontra o ponto mais
alto da torre em relação ao solo?(dados: sen 74º =
a) 55 m
b) 15 m
c) 45 m
DC = x - 38
01. h = 2 m
02. h = 3 m
04. a = (1 + 3) m
08. O triângulo ACD
isósceles
16. O lado AC mede 6 m
é
19. Determine o valor de x e y na figura abaixo:
tg74º = 3,4)
d) 42 m
e) 51 m(R)
15.(UFSC)Na figura, abaixo, determine o valor de x.
AD = x
75o. Determine a largura do rio. (R: 10 20 m)
18.Com base na figura abaixo é correto afirmar:
5  2, 24 .(R: 8,94 m)
0,96¸ cos 74º = 0,28 e
modo que o ângulo CAB mede 75o e o ângulo ACB mede
20(ENEM) Na figura abaixo, que representa o projeto
de uma escada com 5 degraus de mesma altura, o
comprimento total do corrimão é igual a:
BD = y
16.(Unicamp-SP) Uma pessoa de 1,65 m de altura
observa o topo de um edifício conforme o esquema
abaixo. Para sabermos a altura do prédio, devemos
somar 1,65m a:
a) 1,8 m
a) b cos  b) a cos  c) a sen  d) b tg  e) b sen R)
17(FUVEST) Dois pontos, A e B, estão situados na
margem de um rio e distantes 40 m um do outro. Um
ponto C, na outra margem do rio, está situado de tal
b) 1,9 m c) 2,0 m
d) 2,1 m (R)
e) 2,2 m
Questão desafio(Experimento de Eratóstenes): O
filósofo grego Erastóstenes percebeu que, em certo dia
do ano, o sol não fazia sombra sobre a cidade de
Siena(estava exatamente acima dela). Porém, no mesmo
dia, em Alexandria, distante cerca de 5000 estádios de
Siena(cada estádio vale 157,5 metros), havia sombra. A
sombra projetada em Alexandria tinha um ângulo de
cerca de 7,2 graus(aproximadamente 1/50 de uma volta
completa). Com isso, ele determinou o comprimento da
Terra. Reproduza o resultado e determine o
comprimento da Terra(distância total percorrida ao se
dar uma volta no planeta).