Lista de exercícios – Função Trigonométrica - EaD

Lista de exercícios – Função Trigonométrica
1-
Um alpinista deseja calcular a altura de uma encosta que vai escalar.
Para isso, afasta-se, horizontalmente, 80 m do pé da encosta e visualiza o topo
sob um ângulo de 55º com o plano horizontal. Calcule a altura da encosta.
(Dados: sen 55º = 0,81, cos 55º = 0,57 e tg 55º = 1,42)
2-
Uma escada encostada em um edifício tem seus pés afastados a 50 m do
edifício, formando assim, com o plano horizontal, um ângulo de 32º. A altura do
edifício é aproximadamente: (sen 32º = 05299, cos 32′ = 0,8480 e tg 32º =
0,6249)
(A)
28,41m
(B) 29,87m
(C) 31,25 m
(D) 34,65 m
3-
Um avião levanta vôo sob um ângulo de 30º. Depois de percorrer 8 km, o
30° = 0,86, sen 30° = 0,50 e
avião se encontra a uma altura de: (dados:
30°=0,58)
(A)2 km
4-
(B)3 km
(C)4 km
(D)5 km
Uma pessoa de 1,50 m de altura, situada a 100 m de uma torre, avista o
seu topo sob um ângulo de 60° com a horizontal. Qual é a altura da torre? dados:
60° = 0,86, cos 60° = 0,50 e
5-
60°=1,73)
(Unesp-SP) Uma pessoa, no nível do solo, observa o ponto mais alto
de uma torre vertical, à sua frente, sob o ângulo de 30°. Aproximando-se 40 m
da torre, ela passa a ver esse ponto sob o ângulo de 45°. A altura aproximada
da torre, em metros, é:
(A)
6-
44,7
(B) 48,8
(C) 54,6
= sec 60° +
Simplifique o valor da expressão
(D) 60,0
30° −
30°
7-
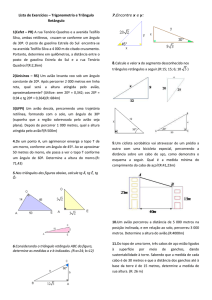
(UNICAMP) Um topógrafo deseja calcular a distância entre pontos
situados à margem de um riacho, como mostra a figura a seguir. O topógrafo
determinou as distâncias mostradas na figura, bem como os ângulos
especificados na tabela abaixo, obtidos com a ajuda de um teodolito.
Calcule a distância entre A e B:
8-
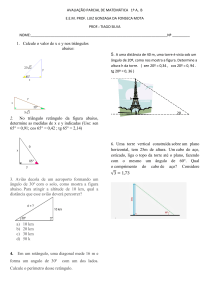
(UNICAMP) Um engenheiro precisa interligar de forma suave dois trechos
paralelos de uma estrada, como mostra a figura abaixo. Para conectar as faixas
centrais da estrada, cujos eixos distam d metros um do outro, o engenheiro
planeja usar um segmento de reta de comprimento x e dois arcos de
circunferência de raio r e ângulo interno α.
a) Se o engenheiro adotar α = 45°, o segmento central medirá
= √2 −
2 √2 − 1 . Nesse caso, supondo que d = 72 m, e r = 36 m, determine a
distância y entre as extremidades dos trechos a serem interligados.
b) Supondo, agora, que α = 60° , r = 36 m e d = 90 m, determine o valor de
x.
9 - Para alcançarmos o 1º andar de um edifício, subimos uma rampa de 6 m que
forma com o solo um ângulo de 30º. A altura desse 1º andar é:
(Considerando: cos 30° =
(A)
3√3
(B)
√!
!
(C)
(D)
√!
,
"
30° = 30° =
√!
)
!
√!
3
10 - Uma pessoa está a 30 m de um edifício e vê o ponto mais alto desse prédio
sob um ângulo de 60°. Sem levar em conta a altura do observador, determine a
altura do edifício. (Dados:sen60° =
(A)
30 3 m
(B)
15 3 m
(C)
15 m
(D)
30 m
√!
"
, cos 60° = 60° = √3).
11- Andar de skate é um esporte preferido de muitos adolescentes em Belo
Horizonte. Descer pelo corrimão de uma escada é um dos grandes desafios
enfrentados por esse público jovem. No desenho, qual é aproximadamente a
distancia que o garoto andou no corrimão, sabendo que o degrau mais alto está
a 2 m do solo, e que o ângulo da escada com o solo é de 30º. (Considerando:
"
30° = , cos 30° =
√!
e
30° =
√!
)
!
( A) 2 3m
( B) 1m
(C ) 4m
( D)
4 3
m
3
12 - Um avião levanta um voo fazendo um ângulo de 60# com o chão.
Considerando que o avião já tenha voado uma distância de 140%& mantendo
este mesmo ângulo, pode-se afirmar que a altura, em %&, que o avião se
encontra do chão neste instante é de: (Considerando:
e
60° =
√!
, cos 60° =
"
60° = √3)
(A) 140√3
(B)
'(
√!
(C) 70√3
(D) 70
13 - O principio da superposição afirma que quando duas ondas se encontram
elas se somam e amplitude resultante dependera da diferença de fase θ entre
-
elas segundo a expressão * = 2 ∙ *( ∙ cos , .. A amplitude resultante terá o maior
valor possível, em módulo, quando o ângulo θ entre as opções abaixo valer:
(A) /
(B)
0
(C) 2/
(D)
!0
1
14 - Um engenheiro fez um projeto para a construção de um prédio (andar térreo
e mais 6 andares), no qual a diferença de altura entre o piso de, um andar e o
piso do andar imediatamente superior é de 3,5 m. Durante a construção, foi
necessária a utilização de rampas para transporte de material do chão do andar
térreo até os andares superiores. Uma rampa lisa de 21 m de comprimento,
fazendo um ângulo de 30° com o plano horizontal, foi utilizada. Uma pessoa que
subir essa rampa inteira transportará material, no máximo, até o piso que se
encontra no: (Considerando:
30# ≅ 0,87,
30# = 0,50 e 30# ≅ 0,58).
(A) 2° andar
(B) 3° andar
(C) 4° andar
(D) 5° andar
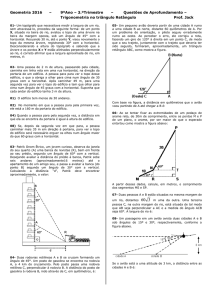
15 - Duas torres ficam de frente uma para a outra, separadas por uma
distância
= 20&. Conforme visto do topo da primeira torre, o ângulo de
depressão da base da segunda torre é 60o e o do topo é 30o (conforme as figuras
abaixo). Considerando:
60# ≅ 1,73e
60# =
30# ≅ 0,87,
30# =
60# = 0,50 e
30# ≅ 0,58; podemos afirmar que a altura da segunda torre é
aproximadamente:
Figura (1)
Figura (2)
(A) 35
(B) 12
(C) 23
(D) 16
16 - Dois participantes de um programa de TV estão na parte plana da Avenida
Afonso Pena, no centro de Belo Horizonte em lados opostos do edifício Acaiaca,
que possui 120 metros de altura. O programa informa a um dos participantes que
o ângulo de elevação do topo do edifício até ele é de 45o e informa também que
o ângulo de elevação do topo edifício ao segundo participante é de 30o. Para
ganhar o prêmio do programa eles precisam dizer qual a distância que existe
entre ambos em linha reta. Qual é este valor?
(A) 308,6 m.
(B) 409,7 m.
(C) 327,9 m.
(D) 189,3 m.
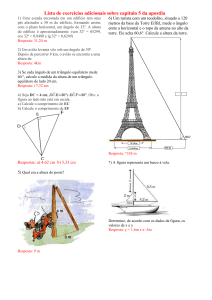
17 – Para determinar a altura de um morro, um topógrafo adotou o seguinte
procedimento:
- Escolheu dois pontos A e B, situados no mesmo plano vertical que passa por
C.
- Mediu a distância AB encontrando 162 m.
- Com auxílio de um teodolito mediu os ângulos 3, 4 5, encontrando
respectivamente, 60⁰, 90⁰ e 30⁰.
A figura ilustra o procedimento descrito
Qual a altura do morro (h), encontrada pelo topógrafo?
(Considerando:cos 30° =
√!
,
"
30° = ,
30° =
60° = √3)
(A)
81 m.
(B)
243 m.
(C)
46,7 m.
(D)
93,4 m.
Respostas
1 113,6&
2) 7
3) 7
4) 174,5&
5) 7
6) 1
7) 5√3
8) a) 72√2 m b) 36√3 m
9. D
√!
, sen 60°
!
=
√!
,
"
60° = ,
10. A
11. C
12. C
13. C
14. B
15. C
16. C
17. A