Aula 01_Tensões verticais.

30/04/2012
Controle de Obras
Mecânica dos solos
• Tensões verticais no solo
Prof. Ilço Ribeiro Jr
1
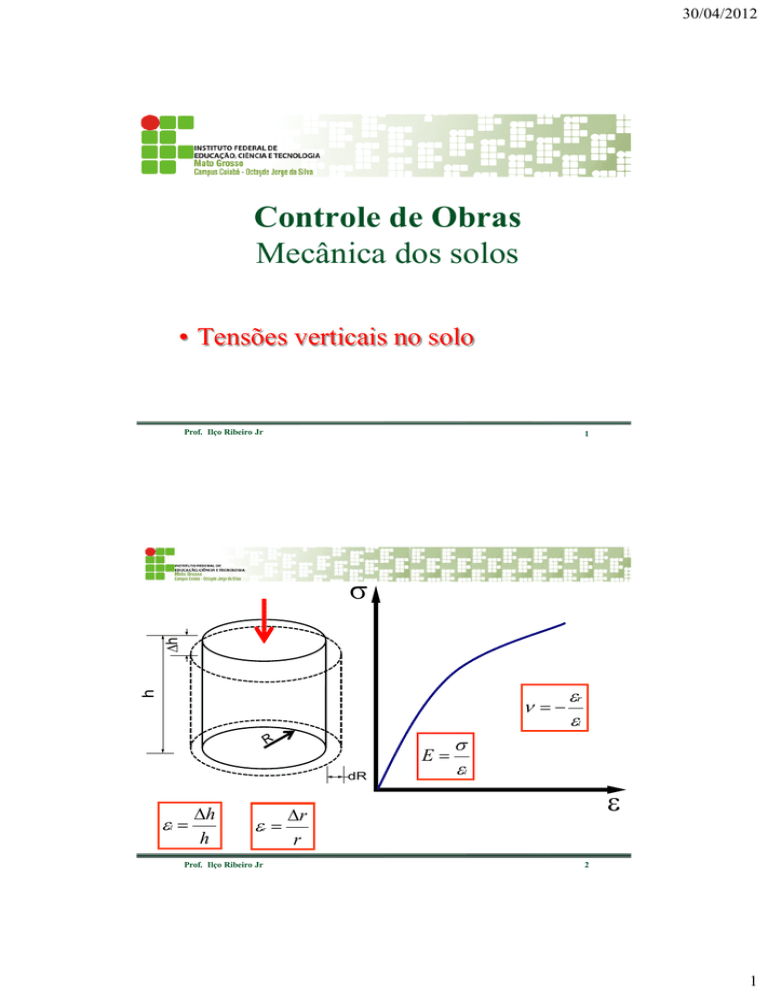
h
Dh
s
 
er
e
l
E
dR
Dh
el 
h
s
e
l
e
Dr
er 
r
Prof. Ilço Ribeiro Jr
2
1
30/04/2012
Prof. Ilço Ribeiro Jr
3
Tensões no Solo
• No solo a tensão vertical em uma determinada profundidade é
devida ao peso de tudo que se encontra acima.
• Ou seja, grãos de solo, água, fundações.
• Desta forma, a tensão normalmente aumenta com a profundidade.
Nível d’água
g  peso específico do solo
zw
z
sz
z
q
sz
Prof. Ilço Ribeiro Jr
sz
sh
sh
sz = gz
z
sz = gz + gwzw
sh
sz = gz + q
4
2
30/04/2012
Tensões no Solo
 Lembre-se que g é o peso de tudo (solo e água) por unidade de
volume.
 Como sz advém do peso total do solo ele é conhecido como tensão
total.
 Note que a água no “lago” mostrado anteriormente aplica uma
tensão total na superfície do solo da mesma forma que a água aplica
um tensão na base de um copo de água.
 O peso específico de solos varia aproximadamente entre 20kN/m3
para um solo saturado e 16kN/m3 para um solo seco. E o peso
específico da água vale 10kN/m3.
 Existem também as tensões horizontais sh, mas não existe uma
relação simples entre sz e sh.
Prof. Ilço Ribeiro Jr
5
Tensões nos solos
Os solos são compostos por partículas. As cargas aplicadas
são transmitidas partículas a partículas além das que são
suportadas pela água dos poros.
No caso de partículas maiores, como grãos de siltes e areias, a
transmissão das forças se dá pelo contato direto mineral com
mineral
Nas argilas as forças nos contatos são muito pequenas mas
pode ocorrer transmissão através da água adsorvida
quimicamente.
Prof. Ilço Ribeiro Jr
6
3
30/04/2012
Diversos grãos transmitirão forças à placa que podem ser
decompostas em normais e tangenciais à superfície da placa.
Porem, é impossível desenvolver modelos que representem
essa situação. Por isso, utiliza-se o conceito de tensões.
N
T
T
N
N
T
Prof. Ilço Ribeiro Jr
7
Fisicamente as tensões serão:
Tensão Normal – Soma das forças normais ao plano
dividida pela área total:
N

s
Area
Prof. Ilço Ribeiro Jr
8
4
30/04/2012
Tensão cisalhante – Soma das forças
tangenciais dividida pela área total:
T


Area
Prof. Ilço Ribeiro Jr
9
A tensão assim definida é muito menor do
que ocorrem nos contatos entre as partículas.
No solo
Nos contatos
Até 1 MPa
Até 700 Mpa
O estado de tensões em qualquer plano passando por um
ponto em um meio continuo é definido por tensões atuantes
em três planos mutuamente ortogonais passando pelo mesmo
ponto.
Prof. Ilço Ribeiro Jr
10
5
30/04/2012
Princípio das Tensões Efetivas
 As tensões em qualquer ponto de uma seção de uma
massa de solo pode ser definida a partir das tensões
principais totais σ1,σ2,σ3 que agem neste ponto.
 Se os vazios do solo estiverem preenchidos por
água, sob pressão u, as tensões totais são compostas
por 2 parcelas:
Prof. Ilço Ribeiro Jr
11
 Uma parcela u que atua na água e nos grãos
sólidos em todas as direções em igual intensidade,
denominada de pressão neutra ou poro pressão;
 A outra partícula é a tensão efetiva que representa
o excesso sobre a pressão neutra, e é suportado
exclusivamente pela parte solida do solo.
s'1  s 1  u
s' 2  s 2  u
s' 3  s 3  u
Prof. Ilço Ribeiro Jr
12
6
30/04/2012
Terzaghi escreveu a equação fundamental do princípio das
tensões efetivas como:
s ' s u
Prof. Ilço Ribeiro Jr
13
A segunda parte do princípio das tensões efetivas diz:
...”Todos os efeitos mensuráveis oriundos da
variação de tensões, tais como compressão,
distorções e mudança na resistência ao
cisalhamento, são exclusivamente devido as
variações da tensão efetiva”...
Prof. Ilço Ribeiro Jr
14
7
30/04/2012
Atkinson e Bransby (1978) apresentaram os seguintes
corolários sobre o princípio das tensões efetivas:
Corolário 1: O comportamento (em termos da engenharia)de 2
solos com a mesma estrutura e mineralogia será o mesmo se eles
tiverem a mesma tensão efetiva.
Corolário 2: Se um solo for carregado ou descarregado, sem
qualquer variação de volume ou distorção, não haverá variação da
tensão efetiva.
Corolário 3: Um solo expandirá em volume (enfraquecendo-se) ou
se comprimirá (tornando-se mais resistente) se a pressão neutra,
isoladamente for aumentada ou diminuída.
Prof. Ilço Ribeiro Jr
15
Tensões no Solo
Água no solo e pressão da água
• A água nos poros de um solo saturado possui uma
pressão conhecida como pressão de poro ou pressão
neutra - u.
Nível de água
Nível de água
hw
hw
u
u  g whw
u
Prof. Ilço Ribeiro Jr
16
8
30/04/2012
Tensão Efetiva
• É claro que a movimentação do solo e a instabilidade dele pode ser
causada por mudanças na tensão total, devida as cargas de fundações ou
escavações em geral.
• No entanto, não é tão obvio que os movimentos do solo possam ser
devido às variações de poro pressão (presão neutra).
• Desta forma, se existe indução de deformação por mudança na tensão
total ou da poro pressão, existe a possibilidade do comportamento do
solo ser governado por uma combinação entre s e u.
• Esta combinação é conhecida como tensão efetiva (s’), por que ela é
efetiva em determinar o comportamento do solo.
• O princípio das tensões efetivas foi estabelecido por Terzaghi em 1923.
s ' s u
Prof. Ilço Ribeiro Jr
17
Climas da Terra
Prof. Ilço Ribeiro Jr
18
9
30/04/2012
Ascenção Capilar
u  g whc
 g w hc
hc
Prof. Ilço Ribeiro Jr
hc
19
Ascenção Capilar
Prof. Ilço Ribeiro Jr
20
10
30/04/2012
Meniscos capilares independentes do nível d’água
A água existente no solo que não se comunica com o
lençol freático forma meniscos capilares como mostra na
figura – chamado de sucção.
T
T
P
P
T
T
Prof. Ilço Ribeiro Jr
21
Nesta situação diz-se que o solo está não-saturado.
A tensão superficial da água aproxima as partículas,
ou seja, aumenta a tensão efetiva.
Essa tensão efetiva confere ao solo uma coesão
aparente que permite construir castelos de areia na
praias. Muitos taludes são estáveis devido a coesão
aparente e por isso ocorrem escorregamentos na época
de chuvas
Prof. Ilço Ribeiro Jr
22
11
30/04/2012
Nesta situação diz-se que o solo
está não-saturado.
Efeito da capilaridade
A tensão superficial da água
aproxima as partículas, ou seja,
aumenta a tensão efetiva.
Essa tensão efetiva confere ao solo
uma coesão aparente que permite
construir castelos de areia na
praias. Muitos taludes são estáveis
devido a coesão aparente e por
isso ocorrem escorregamentos na
época de chuvas
Prof. Ilço Ribeiro Jr
23
Coesão aparente de areias
N.A.
Escavações em areia,
rebaixamento do N.A.
u<0
u=0
u>0
Prof. Ilço Ribeiro Jr
24
12
30/04/2012
solo
não saturado
A Zona Vadosa
poro pressão
negativa
saturado
hcmax.
hcmin.
N.A.
poro pressão
positiva
Prof. Ilço Ribeiro Jr
NA
25
Tensões no Solo
Diagrama de tensões
Diagrama de tensões
0m
argila orgânica mole preta
g = 15 kN/m3
-4m
Tensão Efetiva
areia fina argilosa medianamente compacta
-7m
g = 19 kN/m3
Tensão Total
Pressão Neutra
argila siltosa mole cinza escuro
g = 17 kN/m3
- 15 m
solo de alteração de rocha
Exemplo para a cota –7m
Exemplo para a cota –7m
0
50
100
150
200
250
300
kPa
s  15 * 4  19 * 3  117kPa
u  10 * 7  70kPa
s '  s  u  47kPa
Prof. Ilço Ribeiro Jr
26
13
30/04/2012
Exemplo: Determinação da tensão vertical
A
g=16kN/m³
B
1m
N.A
g=17kN/m³
2m
C
g=20kN/m³
3m
D
Prof. Ilço Ribeiro Jr
27
σv, σv’, u
1m
3m
6m
Prof. Ilço Ribeiro Jr
u
σv’
σv
28
14
30/04/2012
Pto Tensões Totais
Pressão Neutra
Tensões
Efetivas
A
σvA = 0
u A= 0
σ’vA= 0
B
σvB =16x1=
u B= 0
σ’vB=16-0=
16kPa
C
σvC =16+18x2= uC=10x2= 20kPa
52kPa
D
16kPa
σ’vC=52-20=
32kPa
σvD =52+20x3= uD=10x5= 50kPa σ’vD=112-50=
112kPa
Prof. Ilço Ribeiro Jr
62kPa
29
Transmissão de tensões no solo:
Aplicação da Teoria da
Elasticidade
Prof. Ilço Ribeiro Jr
30
15
30/04/2012
Prof. Ilço Ribeiro Jr
31
Aplicabilidade da Teoria da Elasticidade
Para cálculo de tensões
 Massa homogênea – Quando as condições de contorno do
problema analítico se aproxima das condições de contorno “in
situ”, a distribuição de tensões no campo são comparáveis
àquelas obtidas pela análise linear elástica.
Para cálculo de deslocamentos
 O cálculo de deslocamentos depende mais diretamente da
natureza da lei constitutiva e das magnitudes dos parâmetros
utilizados, desta forma, a habilidade da teoria da elasticidade em
prever deslocamentos depende, de forma mais marcante, da não
linearidade e da heterogeneidade do material “in situ”.
 Em outras palavras: quando não existe homogeneidade do
material a teoria da elasticidade não pode ser aplicada.
Prof. Ilço Ribeiro Jr
32
16
30/04/2012
O Problema de Boussinesq
 Espaço semi-infinito
 Material homogêneo
 Massa Isotrópica
 Relação tensão deformação linear
P
x
q
y
r
z
Espaço elástico
Semi-infinito
Prof. Ilço Ribeiro Jr
33
Variação da tensão vertical devida à carga em um ponto
(sz = plotado verticalmente)
(z = constante)
r
(z = constante)
r
(z = constante)
r
(r = 0)
(sz = plotado horizontalmente)
Prof. Ilço Ribeiro Jr
34
17
30/04/2012
Tensão devida à carga em um ponto
Boussinesq
Q
Fator de Influência




3  1 
Ip 


2   r  2 
1
  z  
z
sz
sr
sz 
r
sq
5/ 2
Q
I
2 p
z
Prof. Ilço Ribeiro Jr
35
Espraiamento das tensões
30o
z tg 30
sv 
Prof. Ilço Ribeiro Jr
2L
z tg 30
2L
so
2 L  2 ztg 30o
36
18
30/04/2012
Solução de Newmark
Tensão vertical no canto
de uma área retangular
uniformemente carregada
so
b=n.z
so
a=mz
Z
sz = so.Ir
σv 

sz

0,5
σ0 
2.m.n.(m²  n²  1
2m.n.(m²  n²  1) 0,5 
.
 arctg

4.π  (m²  n²  1  m².n²).(m²  n²  1)
m²  n²  1  m².n² 
Prof. Ilço Ribeiro Jr
37
0.25
0.24
2.0
a=mz
0.23 b=nz
1.5
0.22
1.2
0.21
Tensão vertical no
canto de uma área
retangular
uniformemente
carregada
SOLUÇÂO DE
NEWMARK
1.0
0.2
0.19
0.18
z
0.7
0.17
0.16
Ir
m
0.8
sz
0.6
0.15
0.14
0.5
0.13
0.12
0.4
0.11
0.1
0.3
0.09
0.08
0.07
0.2
0.06
0.05
0.04
0.1
0.03
0.02
0.01
0
0.1
Prof. Ilço Ribeiro Jr
n
1
10
38
19
30/04/2012
Tensão
Na borda
s z  q * Ir
sz
Prof. Ilço Ribeiro Jr
No centro
s z  4* q * Ir
sz
39
20