1) Calcule, em cada caso a seguir, a medida pedida

-
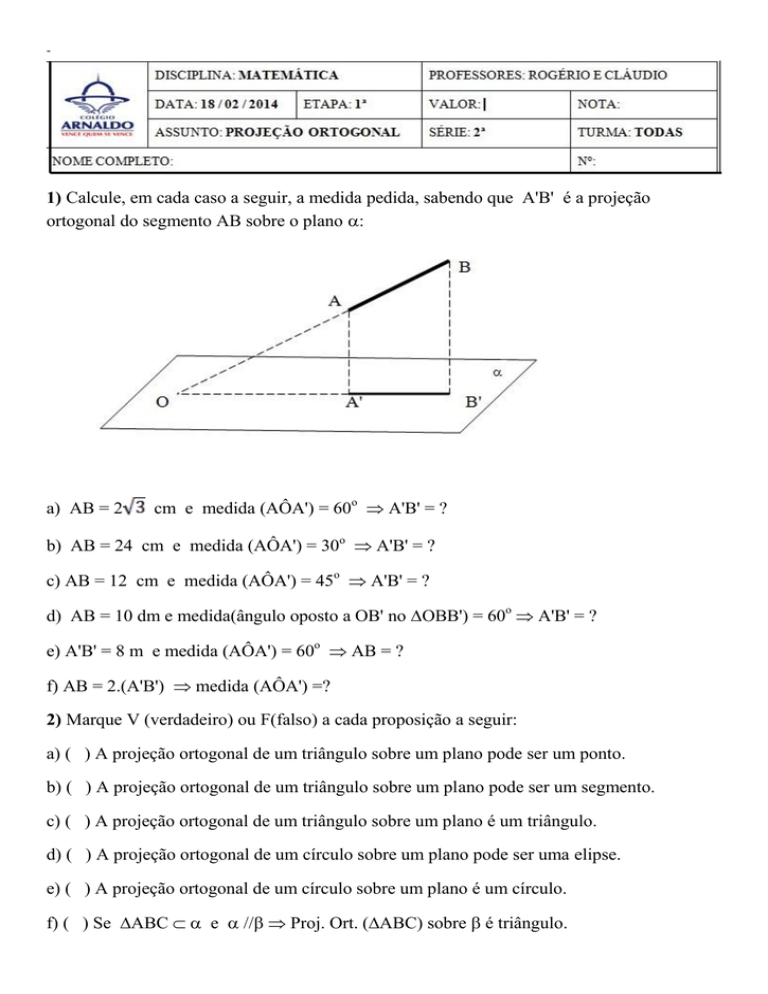
1) Calcule, em cada caso a seguir, a medida pedida, sabendo que A'B' é a projeção
ortogonal do segmento AB sobre o plano :
a) AB = 2
cm e medida (AÔA') = 60o  A'B' = ?
b) AB = 24 cm e medida (AÔA') = 30o  A'B' = ?
c) AB = 12 cm e medida (AÔA') = 45o  A'B' = ?
d) AB = 10 dm e medida(ângulo oposto a OB' no ∆OBB') = 60o  A'B' = ?
e) A'B' = 8 m e medida (AÔA') = 60o  AB = ?
f) AB = 2.(A'B')  medida (AÔA') =?
2) Marque V (verdadeiro) ou F(falso) a cada proposição a seguir:
a) ( ) A projeção ortogonal de um triângulo sobre um plano pode ser um ponto.
b) ( ) A projeção ortogonal de um triângulo sobre um plano pode ser um segmento.
c) ( ) A projeção ortogonal de um triângulo sobre um plano é um triângulo.
d) ( ) A projeção ortogonal de um círculo sobre um plano pode ser uma elipse.
e) ( ) A projeção ortogonal de um círculo sobre um plano é um círculo.
f) ( ) Se ∆ABC   e  //  Proj. Ort. (∆ABC) sobre  é triângulo.
) Se ∆ABC   e  //  Proj. Ort. (∆ABC) sobre  é um segmento.
h) ( ) Se ∆ABC   e    Proj. Ort. (∆ABC) sobre  é um segmento.
i) ( ) Se ∆ABC   e    Proj. Ort. (∆ABC) sobre  é um ponto.
3) Observe atentamente o triângulo ABC e sua projeção ortogonal A'B'C' sobre o plano .
Se med(AÔA') = 45o, med(AÎA') = 60o, med(BÊB') = 30o, calcule o perímetro do triângulo
A'B'C' e sua área, sabendo que os segmentos AB, BC e CA medem, respectivamente 2
cm , 6 cm e 2
cm.
A área de um triângulo com os lados medindo a,b e c é dada pela fórmula de Heron:
A=
em que p =
4) Uma estante tem duas prateleiras planas e paralelas dispostas horizontalmente de modo
que na prateleira superior tem uma lata de refrigerante. Como será a projeção ortogonal da
lata na prateleira inferior se a lata encontra-se
a) de pé na estante?
b) deitada na estante?
5) Observe a peça da figura abaixo:
Nesta peça, o bloco ABCDEFGH, que tem todos os ângulos retos, é colado a uma lata , de
modo que o fundo da lata esteja na face ABCD do bloco citado. Se posicionarmos esta peça,
entre dois planos perpendiculares  e , de modo
a) que o plano da face EFGHE do bloco fique paralelo ao plano , como serão as projeções
ortogonais da peça no plano  e no plano ?
b) que o plano da face EFGHE do bloco fique perpendicular ao plano , como serão as
projeções ortogonais da peça no plano  e no plano ?
6) Ainda no caso anterior, considere um plano , paralelo a , portanto, perpendicular a .
Como serão as projeções ortogonais no plano , em cada um dos posicionamentos do
exercício anterior?
7) Em cada caso a seguir, calcule a medida das projeções desconhecidas no triângulo
ABC, retângulo em A, sendo AH uma altura.
8) Observe o sólido abaixo e algumas de suas projeções ortogonais sobre um plano :
a) Use letras maiúsculas para nomear todos os pontos do sólido.
b) Como foi posicionado o sólido em relação aao plano  para gerar cada projeção
apresentada.
c) A face em primeiro plano do sólido apresenta um segmento inclinado ( de 45o) que mede
12 cm. Com que medida esse segmento terá sua projeção no plano  , se essa face for
perpendicular ao plano ?
9) Um objeto foi colocado entre dois planos perpendiculares  e , como na figura abaixo:
As projeções ortogonais desse objeto no plaano  e no plano  são dadas abaixo. Que
obbjeto é esse?
10) O polígono ABCDEFA é projetado ortogonalmente num plano, dando origem à projeção
A'B'C'D'E'F'A'. Sabe-se que os lados do polígono medem AB =4cm, BC = 6 cm, CD= 3 cm,
DE = 5 cm, EF = 6 cm e FA = 5 cm. por outro lado, os ângulos que os prolongamentos
desses lados formam com o plano de projeção são, respectivamente, 45 o, 30o, 45o, 60o, 60o
e 30o. Calcule o perímetro da projeção.
ÂNGULO FORMADO POR DUAS RETAS REVERSAS
Na figura abaixo, as retas r e s , pertencentes, respectivamente, aos planos  e 
são reversas. Portanto o ângulo formado por r e s é aquele formado por uma delas
e a projeção ortogonal da outra sobre o plano da primeira, observe .
Ângulo entre r e s = ângulo entre r' e s : medida m
Se o ângulo entre duas reversas é RETO (90o), então elas são ORTOGONAIS.
11) A figura abaixo, apresenta quatro planos distintos , ,  e . Sabe-se que  forma um
ângulo de 120o com , 150o com  e é perpendicular a ; por outro lado,  é perpendicular a
 e forma um ângulo de 60o com  e este forma um ângulo de 30o com .
Complete cada proposição abaixo, de modo que ela fique verdadeira:
a) Se r é paralela ao segmento BE e t é paralela ao segmento ED, então as retas r e t formam
um ângulo que mede .......................................
b) Se s é paralela ao segmento JE e t é perpendicular ao segmento JE, então as retas s e t
formam um ângulo que mede .......................................
c) Se r é paralela ao segmento BE e s é paralela ao segmento JE, então as retas r e s formam
um ângulo que mede .......................................
d) Se u e t são perpendiculares ao segmento IF, então as retas u e t formam um ângulo que
mede .......................................
RESPOSTAS :
1) a)
cm
b) 12
cm
c) 6
cm
d) 5
dm
e) 16 m
f) 60o
2) a) F b) V c) F d) V
e) F
3) Perímetro = 8 cm e Área = 2
f) V
g) F
h) V
i) F
cm2
4) a) um círculo ou disco. b) um retângulo.
5) a) Em : um retângulo de medidas iguais a EFGHE. Em : Um "T" invertido.
b) Em : Um "T" invertido. Em : um retângulo de medidas iguais a EFGHE.
6)
7)
8)
9)
a) um círculo dentro de um retângulo, b) Um "T" invertido.
a) CH = 3 cm e HB = 9 cm b) CH = 4 dm e HB = 16 dm
a) resposta pessoal b) resposta pessoal
c) 6 cm
um prisma triangular.
10)
11) a) 60o
cm.
b) 120o
c) 150o
d) 90o