MODELO MATEMÁTICO DO MOTOR DE INDUÇÃO ASSINCRONO

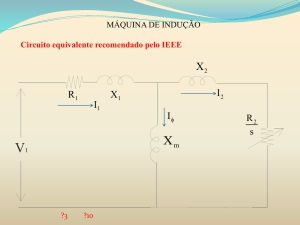
MODELO MATEMÁTICO DO MOTOR DE INDUÇÃO ASSINCRONO
Note que se trata de um modelo de transformador já visto no qual o rotor é o secundário o
qual esta operando a uma freqüência menor f2
Onde:
R1
= Resistência do fio estator
XL1
= Reatância de dispersão primaria ( das bobinas que forman o estator)
E1
= Tensão induzida no estator
E2
= Tensão induzida no rotor
XL2
= Reatância de dispersão secundaria ( no rotor)
R2/s
= Resistência do rotor equivalente a que depende do escorregamento
S=
s  a
s
sωs = ωs - ωa
A freqüência no secundário em função da freqüência primaria
f2 = f1s = f1 - fa
A impedância no secundário em função da freqüência primaria
Z2(f2) =
R22  2f 2 L2  ;
Z2(f2)=
R22  (2f1 sL2 ) 2
Z2(f1) =
R22  ( XL2 s ) 2
2
como f2 = f1s
A tensão induzida no secundário em função da freqüência primaria
E2(f2) = 4,44 f2 N2 Ф
(derivando o fluxo), com f2 = f1s
E2(f1) = 4,44 f1s N2 Ф ( tensão secundaria em função de f1)
E2(f2) = E2(f1) s
A corrente secundário em função da freqüência primaria
I2=
E2
Z2
=
E2 s
2
R 
2
s  2    XL2 
 s 
E2
=
2
 R2 
2
    XL2 
 s 
Assim expressando o modelo em função de uma única freqüência o modelo fica:
Refletindo os parâmetros do secundário a traves da relação a2 , obtemos o modelo
simplificado , onde temos a resistência equivalente e a reatância indutiva equivalente.
Obtenção dos parâmetros de um motor
Como se trata de um modelo similar ao um transformador os ensaios são os mesmos que
para um transformador, circuito aberto e em curto circuito.
Refletindo os parâmetros do secundário a traves da relação a2
, obtemos o modelo
simplificado , onde temos a resistência equivalente e a reatância indutiva equivalente.
Com o ensaio de circuito aberto isto é motor a trabalhando a vazio, obtemos as perdas do
núcleo, com o ensaio de curto circuito motor com rotor bloqueado, obtemos as perdidas do
cobre.
Ze =
Vcc
= impedância equivalente ( do ensaio de rotor bloqueado)
Icc
Onde:
Vcc = tensão aplicada no estator com o rotor bloqueado
Icc = Corrente medida no estator com o rotor bloqueado
Wcc = Potencia ativa na condição de rotor bloqueado
Wcc = Icc2 Re
= > Re = resistência equivalente
A reatância equivalente XLe = Ze 2  Re 2
Como
Z1
= a2 => Z1 = a2Z2
Z2
Refletindo os parâmetros do secundário a traves da relação a2, obtemos o modelo
simplificado , onde temos a resistência equivalente e a reatância indutiva equivalente
Re = R1+ a2
R2
s
XLe = XL1 + a2XL2
Igualando
Z1 = a2Z2
R1 = a2
R2
s
( Pelo teorema da máxima transferência de potencia )
( da igualdade entre números complexos)
Por tanto
Re = R1+ a2
R2
s
Re = 2R1 = 2 a2
Assim R1 =
R2
s
Re
,
2
R2 =
Re s
2a 2
Da mesma forma com a parte reativa
XL1 =a2XL2
( da igualdade entre números complexos)
XLe = XL1 + a2XL2
XLe = 2 XL1 = 2 a2XL2
Assim XL1 =
XLe
,
2
XL2 =
XLe
2a 2