Apresentação do PowerPoint

MÁQUINA DE INDUÇÃO
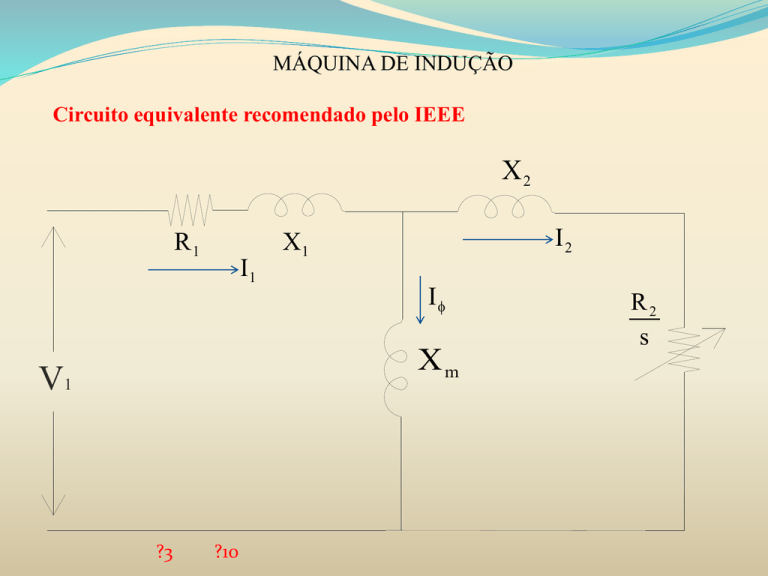
Circuito equivalente recomendado pelo IEEE
X2
R1
I1
I2
X1
I
Xm
V1
?3
?10
R2
s
MÁQUINA DE INDUÇÃO
1.
A corrente de excitação IΦ (corrente que circula pela reatância de
magetização) é alta, da ordem de 30% a 50 % da corrente de plena
carga.
2.
A reatância de dispersão X1 é alta.
3.
A resistência de perdas Rc é omitida e as perdas no núcleo são
concentradas com as perdas por atrito e ventilação.
MÁQUINA DE INDUÇÃO
Circuito Equivalente de Thevenin
X2
X th
R th
I2
R2
s
Vth
V1
?
Air gap
MÁQUINA DE INDUÇÃO
A tensão e a impedância de Thevenin podem ser calculadas da seguinte
maneira:
Vth 
Xm
 R 12   X1  X m 2 


jX m (R1  jX1 )
Z th 
R1  j  X1  X m 
1
2
 V1
MÁQUINA DE INDUÇÃO
TESTE A VAZIO, TESTE A ROTOR BLOQUEADO E PARÂMETROS
DO CIRCUITO EQUIVALENTE
Os parâmetros do circuito equivalente podem determinados do resultado do
teste a vazio, do teste a rotor bloqueado e da medição da resistência cc do
enrolamento do estator.
TESTE A VAZIO
O teste a vazio em uma máquina de indução, assim como o teste de circuitoaberto no transformador fornece informação sobre a corrente de excitação e as
perdas rotacionais.
1.
Teste executado pela aplicação de tensões polifásicas equilibradas no
enrolamento trifásico do estator na frequência nominal.
2.
O rotor é mantido desacoplado de qualquer carga mecânica.
MÁQUINA DE INDUÇÃO
3.
A perda de potência mecânica na máquina operando em vazio é devido à
perda no núcleo e as perdas por atrito e ventilação.
4.
A perda rotacional total na tensão e frequência nominais em carga é
considerada constante e igual ao valor da perda rotacional sem carga.
TESTE A ROTOR BLOQUEADO
O teste a rotor bloqueado na máquina de indução, assim como o teste de curtocircuito no transformador fornece informação sobre as impedâncias de
dispersão.
1.
O rotor é mantido bloqueado (sem girar)
2.
O teste a rotor bloqueado deve ser executado nas mesmas condições de
corrente e frequência que prevalecem na operação normal da máquina.
MÁQUINA DE INDUÇÃO
3. Quando a máquina está funcionando em condição normal, ela opera com
valor de escorregamento baixo, o que significa que a resistência efetiva e a sua
reatância possuem valores diferentes dos valores na frequência nominal.
4. O teste deve ser executado com tensão reduzida e corrente nominal. A
frequência também deve ser reduzida.
5. O IEEE recomenda um valor de frequência de 25% da frequência nominal.
O exemplo a seguir ilustra o procedimento de cálculo para encontrar os
parâmetros do circuito equivalente do motor de indução trifásico recomendado
pelo IEEE.
Os seguintes resultados foram obtidos de motor de indução trifásico, 60 hp,
2200 V, 6 pólos, 60 Hz, do tipo gaiola de esquilo.
MÁQUINA DE INDUÇÃO
1. Teste a vazio
1.1 Frequência: 60 Hz
1.2 Tensão de linha: 2200 V
1.3 Corrente de linha:4,5 A
1.4 Potência de entrada: 1600 w
2. Teste a rotor bloqueado
2.1 Frequência: 15 Hz
2.2 Tensão de linha: 270 V
2.3 Corrente de linha: 25 A
2.4 Potência de entrada: 9000 w
3. Teste de medição da resistência cc do enrolamento do estator por fase:
R = 2,8 Ω
MÁQUINA DE INDUÇÃO
Determine:
a) Perda rotacional sem carga
b) Determine os parâmetros do circuito equivalente recomendado pelo IEEE
c) Determine os parâmetros do circuito equivalente de Thevenin
SOLUÇÃO:
a)
Do teste sem carga, a potência sem carga é:
PNL  1600w
A perda rotacional sem carga é:
PR  PNL  3R 1I12
PR  1600  3  2,8  4,52
PR  1429,9w
MÁQUINA DE INDUÇÃO
b) Para a condição sem carga, R2/s é muito elevada, pois o escorregamento é
baixo.
R NL
X1
I1
Xm
V1
?
MÁQUINA DE INDUÇÃO
Para essa condição, a reatância de magnetização está em paralelo com um ramo
com resistência muito elevada. Pode-se considerar, como o valor resultante
igual ao Xm.
O valor da tensão de entrada por fase no circuito representando o
comportamento em vazio do motor de indução trifásico:
2200
V1 
 1270,2V
3
A impedância sem carga é igual a:
V1 1270,2
Z1 

 282,27
I1
4,5
MÁQUINA DE INDUÇÃO
O valor da resistência sem carga é:
R NL
PNL
1600
 2 
 26,34
2
3I1 3  4,5
A reatância sem carga é:
X NL 
2
2
Z

R
 NL NL 
X NL 
2
2
282,27

26,34

  281
Assim,
X1  X m  X NL  281
?
MÁQUINA DE INDUÇÃO
Para o teste a rotor bloqueado, jXm está em paralelo com ramo que
contém a impedância jX2+R2 .
X2
R1
I2
X1
I1
I
V1
Xm
X m  R 2  jX 2
O ramo central é
desprezado
R2
s
MÁQUINA DE INDUÇÃO
O circuito equivalente adaptado para a condição de rotor bloqueado.
R1
X1
X2
I1
R2
V1
MÁQUINA DE INDUÇÃO
A resistência a rotor bloqueado é:
R BL
PBL
9000


 4,8
2
2
3  I1 3  25
Como a resistência do enrolamento do estator já foi encontrada a partir do teste
de medição de resistência (cc), então:
R BL  R 1  R 2
R 2  R BL  R 1  4,8  2,8
R 2  2
Para o cálculo da impedância, deve-se considerar que a frequência é igual a 15
Hz. Então a reatância que encontrada é com referência a esta frequência.
MÁQUINA DE INDUÇÃO
A impedância a rotor bloqueado é:
Z BL
V1


I1
270
25
3  6,24
A reatância a rotor bloqueado na frequência de 15 Hz é:
X BL 
2
2
Z

R
 BL BL 
X BL 
2
2
6,24

4,8


X BL  3,98
MÁQUINA DE INDUÇÃO
O valor da reatância é 60 Hz:
X BL
60
 3,98   15,92
15
Assim,
X BL 15,92
X1  X 2 

 7,96
2
2
Na frequência de 60 Hz.
Sabemos que X1 + Xm=XNL
X m  X NL  X1  281  7,96  273,04
MÁQUINA DE INDUÇÃO
Características de desempenho
1.
2.
3.
4.
5.
Eficiência
Fator de potência
Corrente
Torque de partida
Torque máximo
O torque mecânico desenvolvido por fase é dado por:
Pmec
R2
 Tmec  I
(1  s)
s
2
2
Onde: (velocidade mecânica)
2n

60
MÁQUINA DE INDUÇÃO
Sabe-se também que:
  (1  s)s
 ns 
   2  (1  s)
 60 
120f
4f1
s 
2 
p60
p
Onde ωs é a velocidade síncrona em rad/s.
MÁQUINA DE INDUÇÃO
Cálculo do torque mecânico (por fase) em função da velocidade síncrona:
R2
Tmec (1  s)s  I
(1  s)
s
 2 R2 
Tmecs   I 2
 Pag

 s 
1
1
Tmec 
Tmec  Pag
s
s
2
2
Do circuito equivalente de Thevenin:
[3]
 2 R2 
 I 2 s 
MÁQUINA DE INDUÇÃO
Do circuito equivalente de Thevenin:
Tmec
1

s 
R2
 R th  s

2
th
V
2
  X X 2
  th
2

R2
s
O torque acima é por fase. Para encontrar o torque total trifásico é
preciso multiplicar por três.
Para valores baixo de escorregamento, tem-se que:
MÁQUINA DE INDUÇÃO
Para valores baixo de escorregamento, tem-se que:
R2
R th 
X th  X 2
s
R2
R th
s
1 Vth2
Tmec 
s
s R 2
MÁQUINA DE INDUÇÃO
TORQUE MÁXIMO – COMO ENCONTRAR?
Uma expressão para o torque máximo pode ser encontrada derivando a fórmula
do torque mecânico em relação ao escorregamento.
R2
s T max

R
2
th
  X th  X 2 
2

escorregamento correspondente ao torque máximo
MÁQUINA DE INDUÇÃO
TORQUE MÁXIMO
Tmax
1
Vth2

2s R  R 2   X  X 2
th
th
th
2