Aula 5-Pitágoras-trigonometria[1]

1
CENTRO UNIVERSITÁRIO NOSSA SENHORA DO PATROCÍNIO
Faculdade: INSEAD
Curso: Engenharia da Produção
Disciplina: Introdução ao cálculo
Prof. Paulo César Oliveira
Aula 5-Pitágoras-trigonometria.doc1
TRIÂNGULO DE PITÁGORAS
Pitágoras, matemático, filósofo, profeta, nasceu na ilha de Samos, na Grécia, no século
VI a.C. Existem muitos pontos obscuros sobre a sua história, mas, segundo alguns relatam,
ele teria viajado pelo Egito e Babilônia, período durante o qual assimilou informações sobre
Matemática e Astronomia, juntamente com várias idéias religiosas. Após retornar à Grécia
fundou a Escola Pitagórica.
É atribuída a ele a elaboração da primeira demonstração geral de uma propriedade
muito especial presente num tipo de triângulos também especial – o triângulo retângulo, que
contém um ângulo de 90º. “O quadrado da hipotenusa é igual à soma dos quadrados das
medidas dos catetos”, tanto é que hoje tal propriedade é conhecida como “Teorema de
Pitágoras”. Mas existem documentos históricos demonstrando que casos particulares desse
teorema já eram do conhecimento dos egípcios e babilônios muito antes dos gregos.
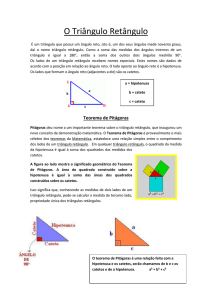
Vejamos uma representação gráfica, com os respectivos nomes de cada lado de um
triângulo retângulo.
Como vemos nas figuras acima, catetos são os dois lados (lados menores do triângulo)
que formam um ângulo de 90º, enquanto a hipotenusa (lado maior) é o lado oposto a esse
mesmo ângulo, e que liga as duas extremidades dos catetos.
A seguir, apresentamos um exemplo cuja hipotenusa (a) mede 5cm, um cateto (b) mede 4
cm e o outro cateto (c) que mede 3 cm:
1
A partir desta aula vou colocar o mesmo título tanto na nota de aula quanto na nomeação do arquivo.
2
Uma maneira de demonstrar o Teorema de Pitágoras é observar que dada uma unidade
de medida de área, podemos construir sobre cada lado do triângulo retângulo um quadrado
correspondente. Então podemos perceber que, ao somamos o resultado do quadrado do
cateto b com o resultado do quadrado do cateto c encontramos 25, que é exatamente igual
ao quadrado da hipotenusa a (escreva esta relação matemática):
ATIVIDADES
1) Se três números inteiros positivos a, b e c tornarem verdadeira a relação a2=b2 +c2, os
mesmos são chamados de números pitagóricos. O menor deles é chamado de áureo
pitagórico (identifique-o). Dê dois outros exemplos.
2) Um carpinteiro quer construir uma escada, de modo que, afastada, no máximo, 2 m de uma
parede, alcance uma janela a 3 m do chão. Qual deve ser o comprimento mínimo dessa
escada?
3) Vamos designar a letra a como a unidade de comprimento das arestas de um cubo. Em
função de a, escreva a relação matemática da medida da diagonal do cubo.
4) Este problema consta do livro Lilavati, escrito pelo matemático hindu Bháskara (século
XII). Se um bambu de 32 m de altura é quebrado pelo vento, de modo que a ponta encontre
o chão a dezesseis metros da base, a que altura a partir do chão ele foi quebrado?
3
5) Calcule a distância entre A (2, 3) e B(6, 6).
6
B
y
A
3
x
2
6
6) (COTUCA 2002) A hipotenusa de um triângulo retângulo mede 13 cm e um de seus
catetos, 5 cm.
a) Calcule o perímetro do triângulo.
b) Determine a sua área.
Relações trigonométricas
O Teorema de Pitágoras deve ser interpretado como uma relação métrica, enquanto
seno, cosseno, tangente, cotangente, cossecante e secante devem ser tratadas como
relações trigonométricas (qual a diferença?). Estas últimas relações serão abordadas
tanto no triângulo retângulo quanto no ciclo trigonométrico.
Com base nesse triângulo de hipotenusa = a, cateto oposto = b e cateto adjacente = c,
temos:
b
op
=
a
hip
c
adj
cotg  =
=
b
op
sen  =
c
adj
=
a
hip
a
hip
sec  =
=
c
adj
cos  =
b
op
=
c
adj
a
hip
csc  =
=
b
op
tg  =
Se elevarmos ao quadrado o sen  e cos  e somarmos seus resultados, formamos uma
equação que representa a relação fundamental da trigonometria (mostre isto).
Antes de passarmos para o ciclo trigonométrico, vamos mostrar como determinamos o
valor de cada uma destas relações, dado os seus ângulos notáveis (300, 450 e 600).
No caso dos ângulos de 300 e 600 vamos levar em conta o triângulo eqüilátero de lado
12. No caso do ângulo de 450 vamos levar em conta um quadrado de lado 2.
Vale ainda ressaltar que neste momento é conveniente trabalhar com os ângulos nas
unidades graus (0 ) ou radianos. Na conversão das unidades temos a seguinte relação: 1800
equivale a  radianos.
2
Note que poderíamos levar em conta o valor genérico l (vamos discutir isto em sala de aula)
4
Com o auxílio das figuras acima, complete os valores da tabela a seguir:
Radianos
Graus
Seno
Cosseno
Tangente
Secante
Cossecante
Cotangente
30
45
60
Passamos agora para o ciclo trigonométrico:
Sen = OB (ordenada do ponto P)
Cos = OA (abcissa do ponto P)
Tg = CE
Cotg = DF
OE = OF representa o raio unitário do
cilo trigonométrico
Na figura a seguir apresentamos os múltiplos dos ângulos de 30, 45, 60 e 90 graus,
distribuídos ao longo dos 4 quadrantes. Em função dos eixos que compõem o plano
cartesiano, o valor das relações trigonométricas são influenciadas pelo estudo de sinal de
cada uma delas.
5
7) (COTUCA 2005) Nas Olimpíadas de Atlanta/1996, o vôlei de praia fez sua estréia em
Olimpíadas. No feminino, duas duplas brasileiras fizeram a final. Um campo de vôlei tem o
formato retangular com dimensões 16m por 8m.
a) Calcule a área desse campo.
b) Duas jogadoras, A e B, em um
determinado momento de um jogo, estão
posicionadas como na figura acima. Calcule
a distância “d” que a jogadora A deve
percorrer para se deslocar paralelamente
à linha lateral, colocando-se à mesma
distância da rede em que se encontra a
jogadora B. (Dados: sen40º = 0,64; cos40º
= 0,77 e tg40º = 0,843).
8) Considere uma volta completa (3600) e determine os possíveis valores do ângulo  :
a) sen  = 1
b) cos  = 0
c) tg  = -1
d) sec  = 0
e) sen  = -
3
2
f) cos  = -
2
2
9) Qual o maior valor que a função seno pode assumir?
10) Qual o menor valor que a função seno pode assumir?
11) De acordo com a resposta da questão 9 e 10, como podemos expressar matematicamente
a variabilidade da função seno?
12) Faça o mesmo para a função cosseno.
13) Calcule o valor de x para cada equação trigonométrica:
a) x- sen1350 + tg
3

=2
6
b) cos
5
- 2x+ csc2700 = 1
4
c) 3.tg

x
+ cotg 1500 +
= -1
3
4
Qualquer ângulo diferente daqueles notáveis será fornecido o valor de suas relações trigonométricas.