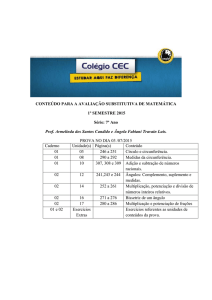
ROTEIRO DE RECUPERAÇÃO DO 1º BIMESTRE – MATEMÁTICA
Nome:
Nº
Data:
/_
Nota:
/_
6ºAno
Professores: Décio e Leandro
(Valor 2,0)
1. Apresentação:
Prezado aluno,
A estrutura da recuperação bimestral paralela do Colégio Pentágono pressupõe uma revisão
dos conteúdos essenciais que foram trabalhados neste ano.
O roteiro de recuperação vai auxiliá-lo a planejar e organizar seus estudos. Para isso,
sugerimos que:
Anote tudo o que tiver para fazer. Fazer um esquema pode ajudar.
Faça um planejamento de estudos, estabelecendo um horário para desenvolver
as diversas tarefas. Planejar significa antecipar as etapas que você precisa fazer
e entregar; não deixe para depois o que pode ser feito hoje...
Estabeleça prioridades: onde você tem mais dúvidas? Como se organizar para
resolvê-las?
Para que você aproveite essa oportunidade, é necessário comprometimento:
resolva todas as atividades propostas com atenção, anote em um caderno suas
dúvidas e leve-as para as aulas de recuperação.
Sempre que possível, aproveite a monitoria de estudos. Procure esclarecer
todas as dúvidas que ficaram pendentes no bimestre que passou.
Tudo o que for fazer, faça bem feito!
2. Conteúdos:
Para ajudar na sua organização dos estudos, vale lembrar quais foram os conteúdos
trabalhados neste ano:
I.
Números naturais e sistemas de numeração (Capítulo 1);
II.
Operações fundamentais com números naturais (Capítulo 2);
III.
Potenciação, raiz quadrada e expressões numéricas (Capítulo 4) e
IV.
Sólidos geométricos, regiões planas e contornos (Capítulo 3 – itens 1, 2 e 7).
3. Objetivos:
Números
naturais e
sistemas de
numeração
Operações
fundamentais
com números
naturais
Perceber o uso social dos conhecimentos matemáticos;
Reconhecer os números naturais em diferentes contextos cotidianos e históricos;
Conhecer antigos Sistemas de Numeração.
Associar ideias, algoritmos e propriedades às operações com números naturais;
Analisar, interpretar, formular e resolver situações-problema envolvendo as
operações com números naturais.
Associar ideias, algoritmos e propriedades à potenciação e à raiz quadrada de
números naturais;
Analisar, interpretar, formular e resolver situações-problema envolvendo as
potenciação e raiz quadrada de números naturais;
Calcular o valor de uma expressão numérica.
Reconhecer e diferenciar as diferentes figuras geométricas, planas e espaciais;
Reconhecer e diferenciar os diferentes poliedros, bem como identificar seus
elementos: vértices, faces e arestas;
Associar poliedros às respectivas planificações;
Reconhecer e aplicar regularidades existentes entre o número de vértices, faces e
arestas dos poliedros;
Reconhecer e diferenciar os diferentes corpos redondos;
Associar os corpos redondos às respectivas planificações;
Reconhecer e classificar regiões planas e contornos;
Relacionar formas geométricas com objetos do cotidiano;
Analisar e discutir quais são as características que permitem classificar os
polígonos em regulares ou irregulares.
Potenciação,
raiz quadrada e
expressões
numéricas
Sólidos
geométricos,
regiões planas e
contornos
4. Materiais que devem ser utilizados e/ou consultados durante a recuperação:
Livro didático: caps. 1, 2, 3 e 4;
Caderno de Atividades;
Listas de estudos;
Anotações de aula feitas no próprio caderno;
Provas mensais 1 e 2;
Prova bimestral.
5. Etapas e atividades que fazem parte do processo de recuperação:
a) refazer as provas mensais e bimestral para identificar as dificuldades encontradas e
aproveitar os momentos propostos para esclarecer as dúvidas com o professor ou
monitor da disciplina;
b) refazer as listas de estudos;
c) revisar as atividades realizadas em aula, bem como as anotações que você fez no
caderno;
d) fazer os exercícios do roteiro de recuperação.
6. Trabalho de recuperação e forma de entrega:
i.
Após fazer as atividades sugeridas para o processo da recuperação paralela,
entregue os exercícios do roteiro de estudos em folha de bloco.
ii.
O Trabalho de recuperação vale 2 pontos.
iii.
Para facilitar a correção, organize suas respostas em ordem numérica. Não apague
os cálculos ou a maneira como você resolveu cada atividade; é importante saber
como você pensou!
iv.
É muito importante entregar o Trabalho na data estipulada.
7. Seguem abaixo as revisões e os exercícios de recuperação:
A primeira parte da revisão trata das 6 operações vistas nesse bimestre (adição,
subtração, multiplicação, divisão, potenciação e radiciação).
Trataremos desse assunto em 4 etapas:
- Aprendendo as operações;
- Expressões numéricas com as operações;
- Problemas com as operações;
- Sólidos geométricos, regiões planas e contornos.
Etapa 1 – Aprendendo as operações
No momento trabalharemos uma revisão para aprimorarmos os métodos para realizar
as operações de multiplicação e divisão. Além disso, seguiremos com as definições de
potência e raiz quadrada.
1.1 Multiplicação
A multiplicação nada mais é do que a soma sucessiva de uma certa parcela. Por
exemplo, 3x4 é o mesmo do que 4 + 4 + 4 + 4 = 12.
Você pode encontrar uma explicação também na Academia Khan https://pt.khanacademy.org/math/arithmetic/multiplication-division/mult-divconcept/v/multiplication-intro
Exercício 1 – Realize as multiplicações de acordo com a ideia acima.
a)
5x12
b)
2x93
c)
4x107
d)
13x15
Ao realizarmos a multiplicação do item e do exercício anterior podemos perceber que,
embora a ideia por trás de uma multiplicação seja muito simples, a execução nem sempre é
fácil. Para esses casos, e outros ainda mais complexos, podemos utilizar um algoritmo
(sequência de passos) que facilite nosso trabalho.
A sequência de passos a seguir trabalha a propriedade distributiva da multiplicação
(Recordar na página 50).
Por exemplo, no caso de 13x15, posso encarar a multiplicação da seguinte forma:
10 x 15 + 3 x 15, pois podemos escrever 13 como 10 + 3. Então 13 x 15 = 10x15 + 3
x15 = 150 + 45 = 195.
Você provavelmente já viu essa mesma ideia em outra disposição.
Repare que as contas são as mesmas. Na figura abaixo destacaremos os passos.
Vamos deixar mais um exemplo. Mas com uma multiplicação de três casas decimais.
A conta que faremos será 124 x 587.
Exercício 2 - A partir do algoritmo visto realize as multiplicações abaixo.
a)
97 x 44
b)
176 x 23
c)
14 x 1091
1.2 Divisão
Quando pensamos em dividir automaticamente pensamos em distribuir quantidades
iguais. Por exemplo, quando pensamos em 20: 4, podemos pensar em 20 repartido em 4
partes igualmente, ficando 5 em cada parte.
Mas nem sempre será tão fácil. Existem casos em que os números envolvidos são
muito grandes, e outros em que a distribuição não é exata, sobrando algum resto.
Antes de prosseguir, vamos relembrar a nomenclatura em uma divisão a partir de um
exemplo.
Seguem três ideias para auxiliar nesses casos. (os trechos a seguir foram tirados do
material didático Telaris páginas 55 até 57)
Aqui utilizaremos o método de estimativa para realizar a divisão de 532 por 14.
Como visto nos casos acima, algumas divisões são exatas e outras não, sobrando
algum resto ao final.
Exercício 3 – Efetue as divisões propostas e identifique quais são divisões exatas.
a) 196 : 4
b) 297 : 3
c) 595 : 7
d) 348 : 6
Exercícios 4 – Efetue as divisões. Identifique o quociente e o resto.
Pensando um pouco mais sobre o resto, podemos dizer que ele sempre será menor
que o divisor.
Pense em uma divisão por 2. Os possíveis restos são 0 ou 1, pois se sobrasse 2
poderíamos continuar a divisão.
Vejamos na prática.
Temos 8 bolinhas vermelhas e as dividiremos em dois recipientes.
Supondo que eu tivesse percebido que teremos apenas 3 para cada lado.
Sobrariam duas ainda, que eu poderia distribuir nos dois recipientes, ficando no total
com 4 em cada recipiente.
Exercício 5 – De acordo com as ideias vistas, responda as questões abaixo.
a)
Quais são os possíveis restos de uma divisão por 13?
b)
Quantos são os possíveis restos de uma divisão por 9?
c)
Somando os possíveis restos de uma divisão por 4, obterei
qual resultado?
1.3 Potenciação
A potência nada mais é do que a multiplicação sucessiva de um mesmo fator. Mas
antes de vermos alguns exemplos, vamos nos focar na nomenclatura.
Base: fator que será repetido na multiplicação.
Expoente: indica a quantidade de vezes que repetiremos a base.
Potência: resultado.
Exemplos:
72 = 7x7 = 49
123 = 12x12x12 = 1728
Perceba que no segundo exemplo, que não é tão imediato, podemos fazer as contas
aos poucos, como na parte de baixo.
A base (o número 12) aparece duas vezes na primeira multiplicação e mais uma vez na
segunda, totalizando 3 repetições, que é o número que aparece no expoente.
LEMBRE - SE
Todo número (diferente de zero) elevado a 0 é igual a 1
Todo número elevado a 1 é igual a ele mesmo.
90 = 1
130 = 1
121670 = 1
1
9 =9
131 = 13
121671 = 12167
Exercício 6 - Calcule as potências
�
) 8³ =
�
) 31² =
�) 400 =
�
) 012 =
Exercício 7 - Sobre o exercício anterior, identifique a base, o expoente e a potência em
cada caso.
Exercício 8 - Escreva em forma de potenciação e calcule.
a) 6 elevado a 3
b) 11 elevado a 2
d) 29 elevado ao quadrado
e) 10 elevado ao cubo
1.4 Raiz quadrada
Obter a raiz quadrada de um determinado número é o mesmo que obter o número que
elevado ao quadrado resulta no número inicial.
Vejamos um exemplo.
√25 = 5, pois 5² = 5x5 = 25
Nem sempre a raiz será imediata. Nesses casos podemos ver algumas dicas que nos
ajudarão no processo de encontrar a raiz quadrada.
Dica 1 - Rastreando o número
Tentaremos achar a raiz de √169
169 é um número próximo de 100, e sabemos que √100 = 10.
Portanto o número que procuramos é maior que 10.
Vamos ver se é maior ou menor que 20.
Como 20x20 = 400 e 400 é maior que 169, podemos concluir que o número que
procuramos é menor que 20.
Então queremos um número entre 10 e 20.
Veremos se é maior ou menor do que 15.
Como 15x15 = 225, temos que o número que queremos está entre 10 e 15.
Tentaremos o 13.
13x13 = 169.
Logo √169 = 13.
Você não precisa escrever todos os passos, podendo somente utilizar essa estrutura
para o seu raciocínio.
Dica 2 - Refinar seu rastreamento.
No caso anterior, quando decidimos que o número está entre 10 e 20, poderíamos ter
pensado que 169 termina com 9, deixando apenas como possibilidade os números 13 ou 17.
Vejamos por exemplo porque não consideraríamos 14 como possível raiz.
Multiplicando 14 por 14 sabemos que resultará em um número terminado em 6 mesmo
antes de fazer a conta. Observe a conta incompleta abaixo.
Não importa o que venha a seguir na conta, sabemos que começaremos a primeira
linha com 6 e a segunda linha com 0, fazendo com que o último número seja 6.
Dessa forma para que o número termine em 9 temos que as únicas opções são 3 ou 7.
Observe a tabela abaixo para conferir a informação.
0x0 = 0
1x1 = 1
2x2 = 4
3x3 = 9
4x4 = 16
5x5 = 25
6x6 = 36
7x7 = 49
8x8 = 64
9x9 = 81
Vamos praticar:
Exercício 9 - Encontre as raízes quadradas dos números abaixo.
a)
b)
c)
d)
√49
√324
√625
√361
Exercício 10 - Utilizando as dicas para diminuir os cálculos, descubra a raiz quadrada
nos itens abaixo.
a)
b) Calcule
Calcule √289
sabendo que
que está
está entre
entre 10
10 e
e 20
20
√196 sabendo
Etapa 2 - Expressões numéricas com as operações.
Agora que já praticamos as operações, treinaremos expressões numéricas.
Para realizar uma expressão numérica, basta respeitar as prioridades listadas abaixo.
1 - Parênteses
2 - Colchetes
3 - Chaves
4 - Potência e Raiz
5 - Multiplicação e Divisão
6 - Adição e Subtração
Faremos dois exemplos a seguir, sempre respeitando as prioridades.
OBS: Se aparecem duas operações com mesmo grau de prioridade, por exemplo
adição e subtração, siga a ordem em que aparecem.
Exercício 11 – Resolva as expressões abaixo.
a) 40 – [25 + (2³ - 7)] =
b) 5² + 2³ - 2 x (3 + 9) =
3
c) (√225 − √64) + (3² - 2⁰ ) =
2
d) (√36 + √64 − √169 + √196) :5 =
Etapa 3 - Problemas
3.1 Problemas envolvendo as operações estudadas
Para resolver um problema é importante que tenhamos em mente um roteiro que
estruture nosso pensamento. Dessa forma é importante pontuar algumas etapas.
Quais informações o problema me dá?
O que está sendo perguntado?
Estratégia
Execução da estratégia
Validação da resposta
Vamos expor essa estrutura de pensamento no problema abaixo como modelo.
Exemplo - Gilson possui um terreno de forma quadrada que tem 169 m² de área. Um
belo dia ele resolveu cercar este terreno com 4 fios de arame em cada lado. Sabendo que em
um dos lados há um portão de 5 m de comprimento, quantos metros de arame ele precisará
comprar?
Quais informações o problema me dá?
O que está sendo perguntado?
O problema pergunta quantos metros de fio Gilson precisa para cercar o
terreno em questão, sabendo que daremos quatro voltas.
Estratégia
Primeiro precisamos descobrir qual é a medida do lado do quadrado Calcularemos a raiz quadrada de 169.
Lembre-se que a área do quadrado é calculada elevando o lado do
quadrado a potência de 2. Portanto precisamos encontrar o número que
multiplicado por ele mesmo resulta em 169, ou seja a raiz quadrada de 16.
Depois precisamos descobrir o perímetro do quadrado, mas precisamos
lembrar de tirar a medida do portão, pois não colocaremos fio no portão Multiplicaremos o valor do lado do quadrado por 4 e subtrairemos 5.
Lembre-se que o perímetro do quadrado é a soma de todos os lados.
Como os lados são iguais, basta multiplicar por 4.
Por fim, devemos multiplicar novamente por 4, pois no passo anterior
descobrimos o comprimento do fio para uma volta apenas.
Execução da estratégia
Agora basta seguir o plano traçado.
√169 = 13. Portanto o lado do quadrado é 13.
Como o lado é 13, temos que o perímetro é 4x13 = 52.
Não podemos esquecer o portão que mede 5 m.
52 - 5 = 47.
Assim precisaremos de 74 metros de fio para uma volta. Mas queríamos quatro
voltas.
4x47 = 188
Logo precisaremos de 188 metros de comprimento de fio.
Validação da resposta
Para validar primeiro temos de ler o problema e ver se a resposta não está fora
do contexto.
Depois podemos realizar as operações contrárias para ver se encontramos
alguma falha na resolução.
Se eu tenho 188 metros de fio para cercar um terreno que tem 52 metros de
perímetros menos 5 metros de portão, tenho que ver quantas voltas conseguirei dar
utilizando 47 metros de fio por volta.
Ao efetuarmos a divisão 188 por 47 temos 4 como quociente e 0 como resto.
Portanto conseguimos dar 4 voltas nessas condições, o que faz sentido de acordo com
nossa situação.
Quando você for resolver um problema, não precisa explicitar cada passo
dessa resolução como no modelo, mas é importante que seu raciocínio fique claro na
resolução. A estrutura anterior tem a intenção apenas de ajudar a direcionar seu
pensamento.
Exercício 12 - Um fazendeiro possui 10 vacas leiteiras. Cada vaca leiteira produz 5 litros
de leite por dia. Se o fazendeiro vender esse leite em garrafas de 1 litro, quantas garrafas podem
ser vendidas em 1 mês?
Exercício 13 - O dono da Pousada Beira – Rio tem 700 reais para comprar frutas para
um café da manhã. Foram gastos 200 reais com pães, 150 reais com frutas, 120 reais com sucos
e 100 reais com frios (queijo, presunto, salame...). Para essa compra, qual será o troco para o
dono da pousada?
Exercício 14 - Comprei um carro por R$ 2.500,00 de entrada mais 24 prestações mensais
de R$ 630,00. Ao final dos 24 meses, quanto terei pago pelo carro?
Exercício 15 - Duas dúzias de estojos custam R$ 384,00. Quanto custa 11 estojos?
Exercício 16 - Qual é a medida do lado de um quadrado que possui 529m² de área?
Exercício 17 - Com a ideia de fazer exercícios físicos Cascão e Magali decidiram limitar
o uso do elevador por semana. Cascão poderia utilizar o elevador 5 vezes por semana enquanto
Magali utilizaria 11 vezes por semana, isso porque Magali mora 5 andares acima de Cascão que
mora no 4º andar. Ambos sempre utilizavam o elevador o número máxi mo de vezes por semana.
a) Em 203 dias, quantas vezes cada um utilizará o elevador?
b) Sabendo que em um determinado período de tempo Cascão utilizou o elevador 25 vezes.
Quantas vezes Magali utilizou o elevador nesse mesmo período de tempo?
c) A diferença do número de vezes que Magali pode usar o elevador para o número de vezes
que Cascão pode usar é 6. Se dobrarmos a quantidade de vezes dos dois, qual será a
diferença? E se triplicarmos?
3.2 Problemas envolvendo raciocínio combinatório
O raciocínio combinatório tem a função de nos auxiliar a descobrir quantas opções
temos de fazer uma determinada combinação de escolhas.
Como exemplo, pense na seguinte situação:
Em uma sorveteria existem 3 sabores de sorvete. O cliente pode escolher entre 2 tipos
de casquinha e ao fim existe 2 tipos de cobertura. De quantas formas alguém que escolha 1
sabor, 1 tipo casquinha e 1 cobertura pode tomar seu sorvete?
Para isso vamos separar os dados.
Sabores - 3 (representaremos por S1, S2, S3)
Casquinha - 2 (representaremos por C1, C2)
Cobertura - 2 (representaremos por K1, K2)
Agora montaremos todas as possíveis combinações
Combinação 1
Combinação 2
Combinação 3
Combinação 4
Combinação 5
Combinação 6
Combinação 7
Combinação 8
Combinação 9
Combinação 10
Combinação 11
Combinação 12
Portanto temos um total de 12 combinações.
Nem sempre será necessário fazer essa árvore que exibe todas as combinações>
Quando tratamos de situações com um número grande de opções fica muito trabalhoso
descrever todas.
Perceba que para cada S temos duas opções de casquinha (C1 e C2), e para cada C
temos duas opções de cobertura (K1 e K2).
Como tenho duas opções de casquinhas e para cada uma tenho duas opções de
cobertura, posso dizer que tenho 2x2 = 4 combinações para uma casquinha e uma cobertura.
Repetindo o mesmo raciocínio, tenho 3 opções de sabores, e para ada sabor tenho 3
combinações de cobertura e casquinha, totalizando 3x4 = 12 combinações.
Esse raciocínio pode ser representado da seguinte forma:
Exercício 18 - Há quatro estradas ligando as cidades A e B, e três estradas ligando as
cidades B e C. De quantas maneiras distintas pode-se ir de A a C, passando por B?
Exercício 19 - Para ir ao Clube, Geraldo deseja usar uma camisa, uma bermuda e um
par de tênis. Sabendo que ele dispõe de seis camisas, quatro bermudas e três pares de tênis.
De quantas maneiras distintas poderá vestir-se?
Exercício 20 - Com os algarismos 1, 2, 3, 4, 5 e 6,
a) Quantos números de três algarismos podemos formar?
b) E se não pudermos repetir algarismos, quantos números de 3 algarismos poderemos
formar?
Exercício 21 - Um restaurante oferece, no período do almoço, cinco opções de entrada,
seis opções de prato principal e três opções de sobremesas. Além disto, este
estabelecimento promove um combo, em que o cliente escolhe uma entrada, um prato
principal e uma sobremesa. Agora responda:
a) Quantas opções de combos existem neste restaurante?
b) Arnaldo não gosta de duas das opções de pratos principais. Então quantas opções
de combos ele possui?
c) Joana não pode comer produtos à base de leite. Sabendo que três entradas, um
prato principal e duas sobremesas possuem produtos à base de leite em suas
receitas, quantas opções de combos ela terá?
3.1 Problemas envolvendo operações inversas
Duas operações são inversas quando aplicadas em seguida retornam ao número
inicial. Como exemplo tomaremos 5 como número inicial.
5+2=7e7-2=5
Se somarmos um número e em seguida subtrairmos o mesmo número, sempre
retornaremos ao número inicial. Portanto adição e subtração são operações inversas. Outras
duas operações inversas são a divisão e multiplicação.
Faremos uso das operações inversas para resolver os dois exemplos abaixo.
Exemplo 1 - Quero descobrir o número que multiplicado por 15 resulta em 105.
Solução
Podemos representar o número que queremos por um triângulo.
∆ x 15 = 105
Dessa forma para descobrir o número em questão basta aplicar a operação inversa
105 : 5 = 21.
Exemplo 2 - No meio do campeonato regional o time de vôlei União Pentagonal trocou
de técnico. O novo comandante, técnico Sami, assumiu o time com uma determinada
pontuação e após 5 rodadas conquistou mais 12 pontos. Desse momento até o fim do
campeonato o time União Pentagonal triplicou sua pontuação chegando aos incríveis 60 pontos
e encerrando com o título tão almejado.
Sabendo dessas informações descubra com quantos pontos Sami assumiu a direção
do time União Pentagonal.
Solução
Podemos pensar da seguinte forma:
Um determinado número somado a 12 e multiplicado por 3 resultou em 60.
Utilizando a ideia de operação inversa, descobriremos o número do meio.
Continuaremos utilizando a ideia de operação inversa para descobrirmos o número
inicial.
Portanto Sami assumiu o time de vôlei com 8 pontos.
Exercício 22 - Descubra o valor do ∆.
a) ∆ + 121 = 873
b) ∆ - 89 = 237
c) 135 - ∆ = 55
d) ∆ x 23 = 92
Exercício 23 - Pensei em um número. Somei 17 e dividi por 11 obtendo 7 como
resultado. Em que número pensei?
Exercício 24 - Maurício foi assistir a um jogo de basquete do Los Angeles Lakers. No
caminho, o pneu do seu carro furou, fazendo com que ele chegasse atrasado. Depois que
Maurício chegou o time marcou mais 15 pontos antes do intervalo e quando voltou para o
último tempo duplicou essa quantidade de pontos atingindo 110 pontos.
Quantos pontos o Lakers possuía quando Maurício chegou ao estádio?
Etapa 4 – Sólidos geométricos, regiões planas e contornos
Estudamos também este bimestre a diferença entre sólidos geométricos, regiões
planas e contornos.
Veja a seguir as definições e exemplos, depois faça os respectivos exercícios.
4.1 Sólidos geométricos
Sólidos geométricos são aquelas figuras de três dimensões: comprimento, largura e
altura. Os sólidos estão divididos em duas principais categorias: poliedros e corpos redondos.
Poliedros são os sólidos que possuem apenas faces planas (não rolam facilmente),
enquanto os corpos redondos possuem uma parte não plana (rolam facilmente).
Os poliedros são divididos em grupos: os prismas e as pirâmides. Os prismas são os
poliedros que possuem duas bases e suas faces laterais são de formato retangular, enquanto
as pirâmides possuem apenas uma base e suas faces laterais são de formato triangular. Veja
abaixo alguns exemplos de prismas, pirâmides e corpos redondos:
Prismas:
O nome do prisma é dado de acordo com a quantidade de arestas de sua base.
Pirâmides:
O nome da pirâmide é dado de acordo com a quantidade de arestas de sua base.
Corpos redondos:
Exercício 25 – Complete a tabela abaixo com a quantidade de vértices, faces e arestas de cada
sólido:
Sólido geométrico:
Quantidade de
Quantidade de
Quantidade de
vértices:
faces:
arestas:
4.2 Regiões planas e contornos
As regiões planas são aquelas figuras de duas dimensões: comprimento e largura. Seu
interior é sempre preenchido (se tentássemos, não conseguiríamos atravessar nossa mão).
Já os contornos são as figuras de apenas uma dimensão: o comprimento. Seu interior
é sempre vazado, isso quer dizer, a figura só possui a borda (se tentássemos, conseguiríamos
atravessar nossa mão).
Veja abaixo alguns exemplos:
Exercício 26 – Na planificação de cada item abaixo, diga quais regiões planas
encontraremos e a quantidade de cada uma delas:
a) Cilindro;
b) Prisma de base hexagonal;
c) Pirâmide de base pentagonal;
d) Prisma de base heptagonal;