Problemas

FÍSICA
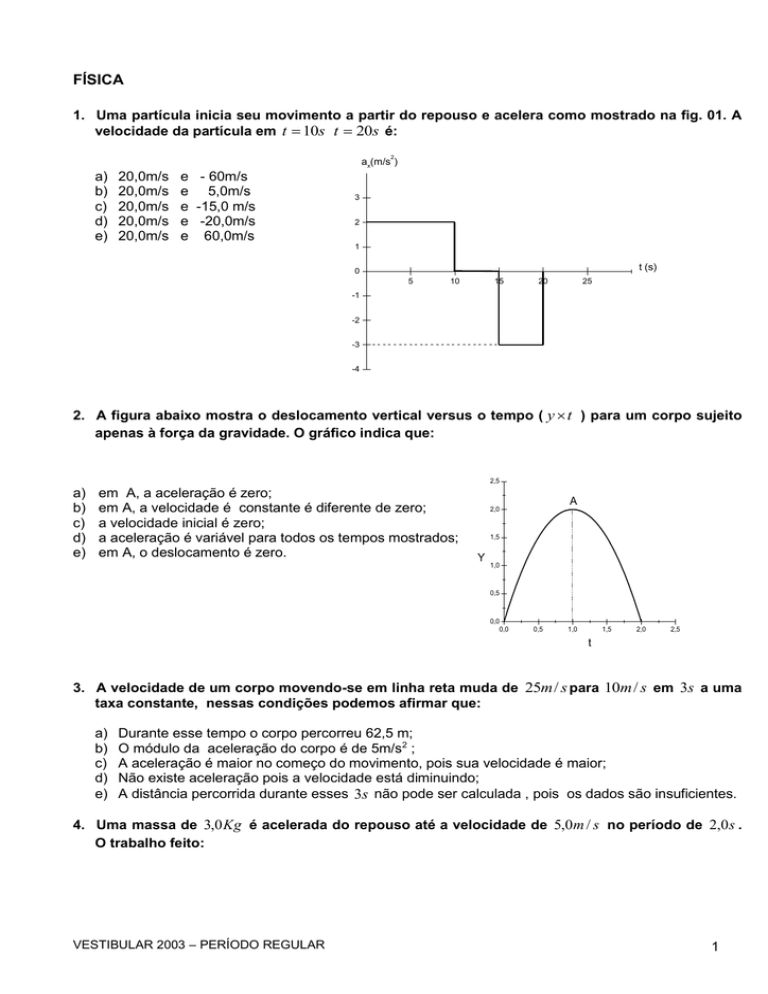
1. Uma partícula inicia seu movimento a partir do repouso e acelera como mostrado na fig. 01. A
velocidade da partícula em t  10s t  20s é:
2
ax(m/s )
a)
b)
c)
d)
e)
20,0m/s
20,0m/s
20,0m/s
20,0m/s
20,0m/s
e - 60m/s
e 5,0m/s
e -15,0 m/s
e -20,0m/s
e 60,0m/s
3
2
1
t (s)
0
5
10
15
20
25
-1
-2
-3
-4
2. A figura abaixo mostra o deslocamento vertical versus o tempo ( y  t ) para um corpo sujeito
apenas à força da gravidade. O gráfico indica que:
2,5
a)
b)
c)
d)
e)
em A, a aceleração é zero;
em A, a velocidade é constante é diferente de zero;
a velocidade inicial é zero;
a aceleração é variável para todos os tempos mostrados;
em A, o deslocamento é zero.
A
2,0
1,5
Y
1,0
0,5
0,0
0,0
0,5
1,0
1,5
2,0
2,5
t
3. A velocidade de um corpo movendo-se em linha reta muda de 25m/ s para 10m/ s em 3s a uma
taxa constante, nessas condições podemos afirmar que:
a)
b)
c)
d)
e)
Durante esse tempo o corpo percorreu 62,5 m;
O módulo da aceleração do corpo é de 5m/s2 ;
A aceleração é maior no começo do movimento, pois sua velocidade é maior;
Não existe aceleração pois a velocidade está diminuindo;
A distância percorrida durante esses 3s não pode ser calculada , pois os dados são insuficientes.
4. Uma massa de 3,0 Kg é acelerada do repouso até a velocidade de 5,0m / s no período de 2,0 s .
O trabalho feito:
VESTIBULAR 2003 – PERÍODO REGULAR
1
a) para acelerar a massa não pode ser determinado a menos que a força seja conhecida como
função da posição;
b) para acelerar a massa não pode ser determinado a menos que a força seja conhecida como
função do tempo;
c) é 37,5 J ;
d) pode ser zero, uma vez que não existe necessariamente uma força resistiva;
e) não pode ser calculado de forma alguma.
5. Sobre um objeto de massa igual a 0,3kg atua uma força resultante igual a 6 N por um período
de 0,6 s . Pode-se dizer com certeza que:
a)
b)
c)
d)
e)
A força não realiza trabalho;
A força só realiza trabalho se ela for uma força centrípeta;
A força realiza um trabalho aproximadamente igual a 29,4 J ;
A força realiza um trabalho igual a 22,0 J ;
A energia cinética da massa é conservada;
6. A força centrípeta
a)
b)
c)
d)
e)
é qualquer força força que acelera um corpo;
não produz mudança na velocidade;
produz uma mudança em ambos, direção e velocidade de um corpo em movimento;
não produz mudança nem na velocidade e nem na direção do movimento de um corpo;
é sempre uma força elástica.
7. A Terra exerce uma força de 850N em um astronauta quando ele trabalha fora da espaçonave.
A força que o astronauta exerce na Terra é:
a)
b)
c)
d)
e)
350N ;
850N ;
720 N
0( zero ) ;
100N .
8. Uma escala uniforme de comprimento l e peso W = 50 N está encostada numa parede vertical,
lisa. O coeficiente de atrito estático, entre o pé de escala e o solo, é  = 0,40. A tangente do
ângulo mínimo  min tal que a escala não escorregue é aproximadamente igual a:
a)
b)
c)
d)
e)
2,00
1,03
2,50
3,10
1,25
9. Sobre propagação de ondas, podemos afirmar que:
a) As ondas que se propagam em uma corda podem ser consideradas ondas longitudinais;
b) Quando duas ou mais ondas movem-se através de um meio, a função de onda resultante em
qualquer ponto é a soma algébrica das funções de onda das ondas individuais;
VESTIBULAR 2003 – PERÍODO REGULAR
2
c) Duas ondas não podem passar uma pela outra, sem serem destruídas ou mesmo alteradas;
d) Um sólido pode transportar apenas ondas longitudinais;
e) Um fluido pode transportar ambos ondas longitudinais e ondas transversais.
10. Uma onda senoidal propagando-se na direção positiva do eixo dos x tem uma amplitude de
15,0cm , um comprimento de onda de 40,0cm , e uma freqüência de 8,0 Hz .O deslocamento
vertical do meio em t  0 e x  0 também é igual a 15,0cm . O número de onda k , o período T
e a freqüência angular  são respectivamente iguais a:
a)
b)
c)
d)
e)
15,4 rad/cm , 0,125 s e 50,3  rad/s
0,157 rad/cm , 0,125 s e 50,3  rad/s
0,05 rad/cm , 0,125 s e 50,3  rad/s
0,05 rad/cm , 0,125 s e 16  rad/s
0,5 rad/cm , 0,125 s e 50,3  rad/s
11. Duas ondas podem ser representadas em um mesmo ponto pela expressão
E1  E0 sin (t ) e
E2  E0 sin (t   )
Existirá interferência destrutiva nesse ponto se:
a)
b)
c)
d)
e)





0
  /2

 2
 3
12. Quando uma substância, na forma líquida, com a temperatura abaixo da temperatura de
solidificação, mantém seu estado, podemos dizer que ocorreu um:
a) Fenômeno de super-aquecimento;
b) Fenômeno de sobrefusão;
c) Fenômeno de superliquefação;
d) Fenômeno de super-sodilicação;
e) Nenhuma das alternativas acima.
13. O volume de um gás ideal é dobrado em uma expansão livre adiabática. De acordo com a
segunda lei da termodinâmica
a)
b)
c)
d)
e)
Sua energia interna não muda;
a temperatura após a expansão é a mesma que antes da expansão;
sua entropia aumenta;
sua pressão após a expansão é a metade de seu valor inicial;
todas as afirmações acima são corretas.
14. Podemos afirmar que nenhuma compressão adiabática:
a)
b)
c)
d)
e)
A temperatura e a pressão diminuem;
A quantidade de calor trocado com o meio externo aumenta;
A temperatura e a pressão aumentam;
A temperatura diminui e a pressão aumenta;
O volume e a temperatura diminuem.
VESTIBULAR 2003 – PERÍODO REGULAR
3
15. João queria comprar um condicionador de ar, mais no entanto não dispunha de dinheiro. João
então pensou, “se eu colocar a minha geladeira dentro do quarto e abrir a porta com ela
funcionando terei o meu sonhado condicionador de ar”. Do ponto de vista da física, podemos
afirmar que:
a)
b)
c)
d)
e)
A temperatura não diminuirá, João está maluco;
A temperatura diminuirá, João é um excelente físico;
A temperatura permanecerá constante;
A temperatura será nula pois o motor aquece na mesma taxa que o refrigerador retira calor;
Seria duas geladeiras para resfriar o quarto.
16. O Trabalho feito para expandir um fluido do ponto i ao ponto f é igual a :
10 7 J
12  106 J
8  106 J
6  106 J
18  106 J
i
6
Pressão
a)
b)
c)
d)
e)
6x10
6
4x10
2x10
6
f
0
1
2
3
4
5
6
3
Volume (m )
17. N moles de um gás ideal é aquecido de 0º C a Tº C dentro de uma caixa plana (bidimensional),
podemos dizer que sua energia interna será:
3
NRT
2
1
b)
NRT
2
a)
VESTIBULAR 2003 – PERÍODO REGULAR
4
c)
1
RT
2
d)
NRT
3
e)
NT
2
18. O organismo humano pode ser submetido sem conseqüências danosas a uma pressão de no
máximo 4x105 N/m2 e uma taxa de variação de pressão de no máximo 104 N/m2 por segundo.
Nestas condições, qual a máxima velocidade de movimentação na vertical recomendada para um
mergulhador?
Dados: Patm = 105 N/m2
 = 103 Kg/m3
g = 10 m/s2
a)
b)
c)
d)
e)
v = 1,5 m/s
v = 1,0 m/s
v= 0,5 m/s
v = 2,0 m/s
Nenhuma das respostas acima.
19. O elemento ativo de um certo laser é um bastão de vidro de 30cm de comprimento e 1,5cm de
diâmetro. Se a temperatura do bastão se elevar de 65 C, o aumento do volume é:
(Dado: vidro =9 x10-6 ºC-1 p/ o vidro comum)
a) 64,0mm3
b) 93,0mm3
c) 85,0mm3
d) 78,0mm3
e) 64,0mm3
20. Seu olho contém uma lente convergente e uma superfície sensitiva à luz, a retina. Seu olho se
assemelha a uma câmara fotográfica porque:
a)
b)
c)
d)
e)
Ambos formam imagens reais de objetos em superfícies sensitivas à luz;
Ambos formam imagens virtuais de objetos em superfícies sensíveis à luz;
Ambos formam imagens virtuais e invertidas de objetos;
Ambos formam imagens nítidas de objetos situados em determinadas distâncias;
Ambos utilizam um dispositivo para controlar o tempo de interação da luz com as lentes.
21. Dentro da água, uma pessoa sente-se mais leve em virtude da força exercida pela água sobre o
corpo imerso. Esta força é chamada de empuxo e é descrita pela lei de Arquimedes. Com
relação ao empuxo pode-se afirmar que:
a)
b)
c)
d)
e)
É proporcional ao volume de água descolocado;
A direção do empuxo pode ser horizontal;
É igual ao peso do corpo;
Não depende da gravidade ou campo gravitacional;
É sempre menor que o peso do corpo imerso.
VESTIBULAR 2003 – PERÍODO REGULAR
5
22. O índice de refração da água é 1,33 e do ar 1,00. Um feixe de luz incide sobre a superfície da
água fazendo um ângulo de 50° com a horizontal. Sob essas condições
a)
b)
c)
d)
e)
Ele é totalmente refletido;
A parte refletida faz um ângulo de 40° com a horizontal pois 50 ° + 40° = 90°;
A intensidade do feixe refratado é a mesma do raio incidente;
o feixe refratado faz um ângulo cujo seno é igual 0,87;
o feixe refratado faz um ângulo de 50° com a horizontal.
23. A luz proveniente do Sol chega a Terra, isto prova que:
a)
b)
c)
d)
e)
Ela se propaga em linha reta;
Ela se propaga no vácuo;
Ela tem caráter ondulatório;
Ela se propaga em grandes velocidades;
Ela necessita de um meio para se propagar.
24. O valor da carga elementar foi calculado no experimento de:
a)
b)
c)
d)
e)
Coulomb;
Faraday;
Millikan;
Gauss;
Newton;
25. A lei da conservação da carga elétrica:
a) Aplica-se somente a fenômenos macroscópicos;
b) Aplica-se a fenômenos diversos tais como um bastão de borracha carregado por contato e no
decaimento radioativo;
c) Requer que o módulo da carga do próton seja igual à do elétron;
d) Falha no caso de corpos grandes tais como as galáxias;
e) Foi estabelecida por Coulomb.
26. A figura abaixo mostra as linhas de campo elétrico para duas cargas pontuais separadas por
uma pequena distância . A razão
q2
q1
é:
a) 2,0
b) 0,5
5
12
11
d)
6
c)
e) 1,0
27. Observa-se que um próton tem uma energia cinética de 2,0MeV ( 3,6  106 J ). Ele pode ter
adquirido essa energia da seguinte maneira:
VESTIBULAR 2003 – PERÍODO REGULAR
6
a) “caindo” através de uma diferença de potencial de 2 milhões de volts;
b) em uma colisão frontal, quando em repouso, com um outro próton que tinha uma energia cinética
de 2,0MeV ;
c) quando acelerado até uma distância de 0,5 m por um campo elétrico de módulo igual a
4,0  106V / m ;
d) quando acelerado até uma distância de 0,01 m por um campo elétrico de módulo igual a
2,0  108V / m ;
e) todas as afirmativas acima são verdadeiras.
28. Quando um resistor de resistência R  20 é conectado a uma fonte cuja fem é 1,5V , a ddp é
encontrada com sendo igual a 1,0V ; entretanto,
a) a corrente é 75mA ;
b) a resistência interna r é 10,0 ;
c) calor é produzido pela fonte a uma taxa de 5,2  102W ;
d) se a resistência R fosse menor a ddp seria maior;
e) se a resistência r fosse menor a ddp seria menor
29. A capacitância equivalente da combinação abaixo é igual a:
Considere : C1  10F , C1  5,0F e C1  4,0F
a)
b)
c)
d)
e)
7,8F
18,7 F
12,6 F
6,6F
7,3F
VESTIBULAR 2003 – PERÍODO REGULAR
C1
C3
V
C2
7
30. Um capacitor com espaço livre entre suas placas está carregado a uma diferença de potencial
de 200V . Ele então é desconectado de um circuito externo e o espaço entre as placas é
preenchido com um dielétrico. A diferença de potencial agora é de 40V . Podemos então,
afirmar que:
a) A capacitância não foi alterada;
b) A carga foi reduzida a 1
5
de seu valor original;
c) A quantidade de energia armazenada é invariável;
d) A quantidade de energia armazenada aumentou;
e) A capacitância é cinco vezes maior que antes.
MATEMÁTICA
31. Seja o conjunto A, abaixo,
A = 0, 0, 1 , 
1 , 0,1
É correto afirmar que
a) 0  A
b) 0,1  A
c) 0,1  A
d) os elementos de A são 0 e 1
e) o número de subconjuntos de A é 22 = 4
VESTIBULAR 2003 – PERÍODO REGULAR
8
32. Os conjuntos A e B, não vazios, têm, respectivamente, x – 1 e x + 1 elementos. Se o conjunto A x B
tem 6x – 6 elementos, então é verdade que o conjunto
a)
b)
c)
d)
e)
A tem um único elemento
B tem 4 elementos
A tem 4 elementos
B tem mais de 6 elementos
A tem mais de 6 elementos
33. Seja X o conjunto complementar de um conjunto X qualquer, em
Universo U. Então, parte hachuriada do diagrama abaixo corresponde a:
relação
ao conjunto
A
a)
B  C  A
d)
A  B   A  B 
e)
A B C
b) A - B  C 
c)  A  B  C     A  B  C 
34. O número de divisores do inteiro 1800, é:
a)
b)
c)
d)
e)
24
36
48
60
72
35. Sendo a = 1,666..., b = 1,333... e c = 3, então o valor da expressão ( a – b ) . c , é:
1
9
1
b)
3
4
c)
9
a)
VESTIBULAR 2003 – PERÍODO REGULAR
9
d)
8
9
e) 1
36. O valor da expressão abaixo
74 3 .
a)
b)
c)
d)
e)
74 3
é:
Um irracional NEGATIVO
Um irracional POSITIVO
Um racional POSITIVO
Igual a 1
Um inteiro POSITIVO, maior que 1.
37. Dividindo-se o número 22 em partes inversamente proporcionais a 1, 2 e 3, obtem-se os
valores x , y e z, respectivamente. Assim, é correto afirmar que:
a)
b)
c)
d)
e)
O valor de z é maior que tanto o de x como o de y ;
O valor de y é a metade da soma dos dois outros;
O valor de x é igual a soma dos outros dois;
O produto ( x.y.z ) é um número maior que 200;
A soma ( x + y + z ) é diferente de 22.
38. Após um reajuste de 15%, o salário bruto de um empregado passou a ser R$ 862,50.
Sabendo-se que, sobre o salário bruto incide, a todo tempo, um desconto de 10% referente ao INSS,
pode-se afirmar que o salário líquido deste empregado, antes do reajuste, era de:
a)
b)
c)
d)
e)
R$ 800,00
R$ 770,25
R$ 750,00
R$ 675,00
R$ 645,50
39. A função f definida por f ( x ) =
a)
b)
c)
d)
e)
1
x  3 2  x
tem por Conjunto Domínio o intervalo real:
] 2, 3 ]
] 2, 3 [
[ 2, 3 [
( -  , 2 [  ] 3, +  )
(  , 2 ]  [ 3, +  )
40. Seja f uma função real definida por f : |R
VESTIBULAR 2003 – PERÍODO REGULAR
|R
10
Tendo-se que f ( -1 ) = 3, então, f
a)
b)
c)
d)
e)
–1
x
f( x ) = a . x + 2 (a  |R )
(10) tem valor
0
–2
–4
–6
–8
41. O lucro mensal de uma fábrica é dado por L ( x ) =  x2 + 60x – 10 onde x é a quantidade
mensal de unidades fabricadas e vendidas de um certo bem, produzido por esta empresa
e L é expresso em Reais (Obs. : Real  unidade monetária).
O maior lucro mensal possível que a empresa poderá ter é dado por
a)
b)
c)
d)
e)
R$ 890,00
R$ 910,00
R$ 980,00
R$ 1.080,00
R$ 1.180,00
42. O gráfico dado abaixo é o da função real f definida por f ( x ) = a . 2x + b
O valor de a2 + b2 , é, então, dado por:
Y
a)
b)
c)
d)
e)
y=f
3
5
7
9
11
(x)
3
2
1
X
43. A equação exponencial dada por
 
 3 x


x 1
=1
admite duas soluções, x1 e x2 . O valor da soma ( x1 + x2 ) , é:
a) – 1
b) 0
c) 1
d) 2
e) 3
44. Para determinados valores de a e b, reais, tem-se que log ( a + b ) = 10 e log ( a – b ) = 6.
VESTIBULAR 2003 – PERÍODO REGULAR
11
Então, o valor de log
a)
b)
c)
d)
e)
a b
2
2
corresponde a :
30
16
8
4
2

45. O valor do real y definido por
tg ( )  cos(  )
4
y=

sec ( )
3
é dado pelo número
a)
b)
c)
d)
e)
2
1
1/2
1/4
1/8
46. Acerca da função definida pela lei f : |R
x
|R
y = sen2 x – cos2 x
Assim, pode-se afirmar que:
a)
b)
c)
d)
e)
é certamente não periódica
é periódica, de período 2 π
é periódica, de período π
é periódica, de período π / 2
pode ser periódica ou não periódica
47. A igualdade tg x = 1, é válida para:
a)
b)
c)
d)
e)
x
x
x
x
x
=
=
=
=
=
π/4+2kπ (kZ)
π/4+ kπ (kZ)
π/2+2kπ (kZ)
π/2+ kπ (kZ)
3π/4+2kπ (kZ)
48. A igualdade definida pela equação matricial
3 1
 7 2 

 . A  

 2  1
  3  2
é válida se, e somente se, a matriz A for igual a:
VESTIBULAR 2003 – PERÍODO REGULAR
12
 2 0

 1 2
  2 0


 1 2
 2 0


  1 2
  2 0


1 2 
  2  1


2 
 0
a) 
b)
c)
d)
e)
49. Para determinados valores de a, b e c vale a igualdade
1 2 3
6 9 12
a b c
= –21
Então, a matriz A dada por
a b c
2 3 4
1 2 3
tem Determinante de valor
a)
b)
c)
d)
e)
–7
7
–9
12
21
50. O Conjunto-verdade da equação na variável x
3-x
-1
2
x-4
3
-3
VESTIBULAR 2003 – PERÍODO REGULAR
-1
-2
x-5
=0
13
é o conjunto V dado por:
a)
b)
c)
d)
e)
V = {2, 8 }
V = {- 2, 8 }
V = {2, - 8 }
V = {- 2 }
V={8}
51. Em um campeonato nacional de judô, existem 10 (dez) inscritos, cada um de uma cidade diferente do
país. O regulamento do campeonato estipula que cada atleta lutará com cada um dos outros
competidores duas vezes, sendo cada uma das duas lutas na cidade natal de cada lutador.
O número total de lutas do campeonato será de:
a)
b)
c)
d)
e)
45
50
72
90
100
52. Adicionando-se todas as raízes reais da equação ( 1 + x )4 = 16 x2, obtém-se como resultado o número
real :
a)
b)
c)
d)
–6
–5
–4
–5+2
e) – 5
2
2
53. A seqüência ( s – 1, 3s – 1, s – 3 ), onde s é um real, é, nesta ordem, uma Progressão Aritmética de 3
termos. A soma dos termos extremos de tal P.A. é igual a :
a)
b)
c)
d)
e)
5
3
0
–3
–5
54. A seqüência infinita
S = ( 1,
 2 1 1 1 1 1 1
, ,
,
,
, ,
, ...) tem soma de valor
3 2 3
4 6 8 12
a) Zero
1
3
1
c)
2
b)
VESTIBULAR 2003 – PERÍODO REGULAR
14
d)
2
3
e) Infinito
55. Em um paralelogramo, os lados não paralelos medem 10 cm e 10 2 cm, tendo o maior dos ângulos
medida de 135º. A menor de suas duas diagonais, mede, então:
a)
b)
c)
d)
e)
5 2 cm
10 cm
10 2 cm
20 cm
20 2 cm
56. Uma pirâmide de base quadrangular tem esta base com área de 64 cm2. Efetuando-se nesta pirâmide
um corte a 6 cm de altura da base obtém-se uma seção transversal com área de 16 cm2.
A altura da pirâmide, então, é de :
a) 8 cm
b) 10 cm
c) 12 cm
d) 14 cm
e) 16 cm
57. A reta que, no plano cartesiano, passe pelos pontos A ( 1, 1 ) e B ( 2, -1 ) intercepta os eixos das
Ordenadas e das Abscissas, respectivamente, nos pontos :
5
3
)e( ,0)
2
2
3
(0,3)e( ,0)
2
5
(0, )e(3,0)
2
3
(0,
)e(3,0)
2
3
(0,5)e( ,0)
2
a) ( 0 ,
b)
c)
d)
e)
58. A distância entre o ponto P ( 2 , 1) e a reta r de equação
r : 6 x – 8y + 16 = 0
tem o valor de:
a) 1
b) 2
c) 2
d) 3
e) 5
2
2
2
59. Sendo a um número real qualquer dado, então acerca do resultado do limite
Lim
VESTIBULAR 2003 – PERÍODO REGULAR
x + 2a
15
xa
x+a
o mais correto é afirmar que
a)
b)
c)
d)
e)
será sempre um número inteiro;
valerá, sempre, 3/2, qualquer que seja a ;
será de valor 3/2, se a for não nulo;
será indeterminado se a for nulo;
as alternativas c) e d) estão, ambas, corretas.
60. A derivada segunda da função
f ( x ) = x3 + sen x + ex
é a função:
a) f ( x ) = 3x2 + cosx + ex
b) f ( x ) = 6x – cosx + ex
c) f ( x ) = 6x + senx - ex
d) f ( x ) = 6x – senx + ex
e) f ( x ) = 6x + senx + ex
VESTIBULAR 2003 – PERÍODO REGULAR
16