Inequações polinomiais. Gráficos de funções - Imecc

Roteiro da aula
MA091 – Matemática básica
Aula 29 – Inequações polinomiais. Gráficos de funções polinomiais.
1
Inequações polinomiais
Francisco A. M. Gomes
2
Gráficos de funções polinomiais
3
Exercı́cios
UNICAMP - IMECC
Maio de 2017
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
1 / 18
Inequações polinomiais
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
2 / 18
Inequações polinomiais
Inequações polinomiais
Inequações polinomiais
Sinal de uma função contı́nua
Se f é uma função contı́nua, então sempre que f passa de positiva
para negativa, ou de negativa para positiva, ela passa por um ponto em
que f (x) = 0.
Roteiro para a solução de inequações polinomiais
Para resolver uma inequação na forma p(x) ≤ 0 ou p(x) ≥ 0,
1. Determine as raı́zes da equação associada.
Determine as raı́zes da equação p(x) = 0.
2. Crie intervalos.
Divida o problema em intervalos, de acordo com as raı́zes.
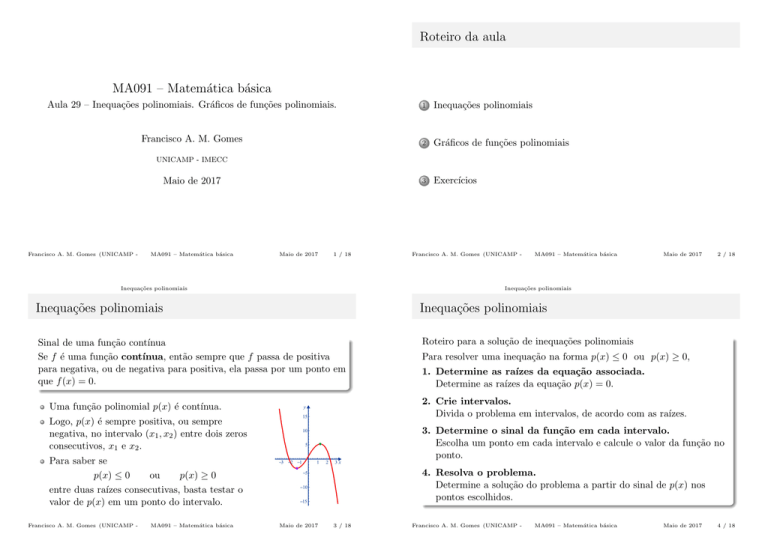
Uma função polinomial p(x) é contı́nua.
Logo, p(x) é sempre positiva, ou sempre
negativa, no intervalo (x1 , x2 ) entre dois zeros
consecutivos, x1 e x2 .
3. Determine o sinal da função em cada intervalo.
Escolha um ponto em cada intervalo e calcule o valor da função no
ponto.
Para saber se
p(x) ≤ 0
ou
p(x) ≥ 0
entre duas raı́zes consecutivas, basta testar o
valor de p(x) em um ponto do intervalo.
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
4. Resolva o problema.
Determine a solução do problema a partir do sinal de p(x) nos
pontos escolhidos.
Maio de 2017
3 / 18
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
4 / 18
Inequações polinomiais
Inequações polinomiais
Exemplo 1
Exemplo 1
x3 + 2x2 − 11x − 12 ≤ 0
Problema
Resolva a inequação
Ponto em cada intervalo:
Em (−∞, −4) : −5
Em (−1, 3) : 0
x3 + 2x2 − 11x − 12 ≤ 0,
sabendo que x = 3, x = −1 e x = −4 são os zeros de
p(x) = x3 + 2x2 − 11x − 12.
Zeros em ordem crescente de valor: −4, −1 e 3
x
p(x)
-5
-2
0
4
-32
10
-12
40
Em (−4, −1) : −2
Em (3, ∞) : 4
Sinal de p(x) = x3 + 2x2 − 11x − 12 em cada
intervalo:
Intervalos:
Solução: {x ∈ R | x ≤ −4 ou − 1 ≤ x ≤ 3}
(−∞, −4), (−4, −1), (−1, 3) e (3, ∞)
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
5 / 18
Gráficos de funções polinomiais
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
Gráficos de funções polinomiais
Caracterı́sticas dos gráficos de funções polinomiais
Caracterı́sticas dos gráficos de funções polinomiais
Continuidade
O gráfico de uma função polinomial é contı́nuo, ou seja, não contém
buracos, saltos (descontinuidades verticais) ou falhas
(descontinuidades horizontais)
Suavidade
O gráfico de uma função polinomial é suave, ou seja, ele não possui
quinas ou bicos (mudanças bruscas de direção ou inclinação).
Com buraco e salto
Com falha
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
6 / 18
Com quina e bico
Contı́nua
Maio de 2017
7 / 18
Definida por partes
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Suave
Maio de 2017
8 / 18
Gráficos de funções polinomiais
Gráficos de funções polinomiais
Comportamento extremo
Comportamento extremo
Tender ao infinito
x tende ao infinito quando x cresce arbitrariamente (assume
valores grandes no sentido positivo do eixo-x):
Teste do coeficiente dominante
Seja an xn o termo de maior grau de p(x). Se
n (grau de p) é ı́mpar
x → ∞.
1
x tende a menos infinito quando x decresce arbitrariamente (se
afasta do zero no sentido negativo do eixo-x):
Se an > 0, então
p → −∞ quando x → −∞
p → ∞ quando x → ∞
x → −∞.
2
A mesma notação pode ser usada para y, se tomamos como referência
o eixo vertical:
y→∞
e
y → −∞.
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
9 / 18
Se an < 0, então
p → ∞ quando x → −∞
p → −∞) quando x → ∞
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Gráficos de funções polinomiais
Maio de 2017
Gráficos de funções polinomiais
Comportamento extremo
Exemplo 2
Teste do coeficiente dominante
Seja an xn o termo de maior grau de p(x). Se
n (grau de p) é par
Problema
Determine o comportamento extremo de cada uma das funções.
1
10 / 18
a) g(x) = −x4 + 3x3 + 16
b) h(x) = x5 + x4 − 10x3 − 4
Se an > 0, então
p → ∞ quando x → −∞
p → ∞ quando x → ∞
2
Se an < 0, então
p → −∞ quando x → −∞
p → −∞) quando x → ∞
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
g(x)
Maio de 2017
11 / 18
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
h(x)
Maio de 2017
12 / 18
Gráficos de funções polinomiais
Gráficos de funções polinomiais
Máximos e mı́nimos locais
Máximos e mı́nimos locais
Pontos extremos de funções polinomiais
Uma função polinomial de grau n tem, no máximo, n − 1 extremos
locais (que podem ser máximos ou mı́nimos).
Pontos extremos e raı́zes de funções polinomiais
Entre dois zeros distintos de uma função polinomial há, ao menos, um
ponto extremo.
Seja dada a função p(x) = 2x3 + 3x2 − 18x + 8.
Os zeros de são x = −4, x =
1
2
e x=2
p(x) possui um ponto extremo em (−4, 21 ) e outro em ( 12 , 2)
p(x) = x3
Embora uma função polinomial possa ter mais de um máximo ou
mı́nimo, as aplicações práticas costumam envolver intervalos só um
ponto extremo faz sentido.
p(x) = −x3 + 5x + 1
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
13 / 18
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Exercı́cios
Maio de 2017
14 / 18
Exercı́cios
Exercı́cio 1
Exercı́cio 2
Problema
Qual é a solução da desigualdade (x + 1)(x − 2)x ≥ 0?
Problema
Relacione as funções aos gráficos.
A) a-2, b-4, c-1, d-3
a) f (x) = x3 − 5x + 1
B) a-4, b-2, c-1, d-3
b) f (x) = −2x3 − x2 + 4x + 6
C) a-3, b-1, c-2, d-4
c) f (x) = x4 − 3x3 − 2x2 + 4x − 4
D) a-1, b-3, c-4, d-2
d) f (x) = 1 − 4x2 − 4x3 + 3x4 + 2x5 − x6
A) x ≤ −2 ou 0 ≤ x ≤ 1
B) x ≤ −1 ou 0 ≤ x ≤ 2
1
2
3
4
C) −2 ≤ x ≤ 0 ou x ≥ 1
D) −1 ≤ x ≤ 0 ou x ≥ 2
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
15 / 18
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
16 / 18
Exercı́cios
Exercı́cios
Exercı́cio 3
Exercı́cio 4
Problema
Determine o número de pontos
√ extremos da função
f (x) = x(x − 3)(x + 2)(x − 2). Indique os intervalos que contêm os
máximos.
√
A) 4 pontos extremos. Máximos nos intervalos (−2, 0) e ( 2, 3)
√
B) 3 pontos extremos. Máximos nos intervalos (−2, 0) e ( 2, 3)
C) 2 pontos extremos. Um máximo em (−2, 0)
D) 3 pontos extremos. Um máximo em (0,
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
√
Problema
Você vai fabricar uma caixa com uma folha de 56 × 32 cm.
1
Escreva as dimensões da caixa em função de x.
2
Escreva V (x) que fornece o volume da caixa em relação a x.
3
Determine o domı́nio de V (x). (Dica: lado ≥ 0).
4
Esboce o gráfico de V (x) usando x = 0, 2, 4, 6, 8, 10, 12, 14.
5
Do gráfico, determine o valor de x que maximiza o volume.
2)
Maio de 2017
17 / 18
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Maio de 2017
18 / 18