Aula 14 - Assíntotas

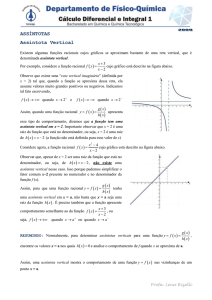
1. Assíntotas verticais e limites infinitos
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
Os limites infinitos para
a função f(x) = 3/(x – 2) podem
escrever-se como
Assíntotas
lim
x → 2−
3
= −∞
x−2
e
lim
x → 2+
3
=∞
x−2
Prof.: Rogério Dias Dalla Riva
4
Assíntotas
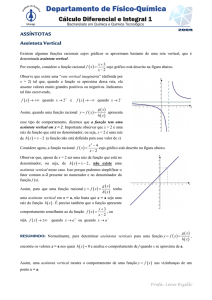
1. Assíntotas verticais e limites infinitos
1.Assíntotas verticais e limites infinitos
Um dos casos mais comuns de assíntota
vertical é o gráfico de uma função racional – isto é,
uma função da forma f(x) = p(x)/q(x), onde p(x) e
q(x) são polinômios. Se c é um número real tal que
q(c) = 0 e p(c) ≠ 0, então o gráfico de f tem uma
assíntota vertical em x = c.
2.Assíntotas horizontais e limites no infinito
3.Assíntotas inclinadas
5
1. Assíntotas verticais e limites infinitos
1. Assíntotas verticais e limites infinitos
Recorde que, a função
f(x) = 3/(x – 2) é não-limitada
quando x → 2. Descrevemos
esse tipo de comportamento
dizendo que a reta x = 2 é uma
assíntota vertical do gráfico
de f. O tipo de limite em que
f(x) → ∞ (ou -∞) quando x → c
pela esquerda ou pela direita é
um limite infinito.
3
Exemplo 1: Determinação de limites infinitos
Limite à esquerda
1
lim
= −∞
x →1− x − 1
Limite à direita
lim
x →1+
1
=∞
x −1
6
1
1. Assíntotas verticais e limites infinitos
1. Assíntotas verticais e limites infinitos
Exemplo 1: Determinação de limites infinitos
Limite à esquerda
−1
lim
=∞
x →1− x − 1
Cada um dos gráficos do Exemplo 1 tem
apenas uma assíntota vertical. Porém, o gráfico de
uma função racional pode ter mais de uma
assíntota vertical.
Limite à direita
lim
x →1+
−1
= −∞
x −1
7
1. Assíntotas verticais e limites infinitos
1. Assíntotas verticais e limites infinitos
Exemplo 1: Determinação de limites infinitos
Limite à esquerda
−1
lim
= −∞
2
x →1− ( x − 1)
10
Exemplo 2: Determine as
verticais do gráfico de f ( x ) = x2 + 2 .
assíntotas
x − 2x
Limite à direita
As assíntotas verticais correspondem aos
valores de x para os quais o denominador é zero.
−1
lim
= −∞
2
x →1+ ( x − 1)
x 2 − 2x = 0
x ⋅ ( x − 2) = 0
x=0 e x =2
11
8
1. Assíntotas verticais e limites infinitos
1. Assíntotas verticais e limites infinitos
Exemplo 1: Determinação de limites infinitos
Limite à esquerda
Limite à direita
Como o numerador de f(x)
1
lim
=∞
2
x →1− ( x − 1)
1
lim
=∞
2
x →1+ ( x − 1)
não se anula em nenhum desses
valores, concluímos que o gráfico
de f tem duas assíntotas verticais
– uma em x = 0 e uma em x = 2.
9
12
2
1. Assíntotas verticais e limites infinitos
2. Assíntotas horizontais
limites no infinito
Exemplo
3:
Determine
verticais do gráfico de f ( x ) =
as
x 2 + 2x − 8
.
x2 − 4
Outro tipo de limite, chamado limite no
infinito, dá um valor finito para o qual tende uma
função quando x aumenta (ou diminui) sem limite.
assíntotas
Fatore primeiro o numerador
denominador, e cancele os fatores comuns.
e
x 2 + 2 x − 8 ( x + 4) ⋅ ( x − 2) ( x + 4) ⋅ ( x − 2) ( x + 4)
f (x) =
=
=
=
,
x2 − 4
( x + 2) ⋅ ( x − 2) ( x + 2) ⋅ ( x − 2) ( x + 2)
e
o
Definição de assíntota horizontal
x≠2
Se f é uma função e L1 e L2 são números
reais, as afirmações
lim f ( x ) = L1
x →∞
e
lim f ( x ) = L2
x →−∞
denotam limites no infinito. As retas y = L1 e
y = L2, são assíntotas horizontais do gráfico de f.
13
1. Assíntotas verticais e limites infinitos
16
2. Assíntotas horizontais
limites no infinito
e
A figura ao lado mostra duas
maneiras como o gráfico de uma
função pode tender para uma ou mais
assíntotas horizontais. Note que o
gráfico de uma função pode cortar
suas assíntotas horizontais.
Para todos os valores de
x ≠ 2, o gráfico desta função
simplificada é o mesmo que o
gráfico
de
f. Podemos, assim,
concluir que o gráfico de f tem
Ao determinar assíntotas horizontais, podemos utilizar a propriedade
apenas uma assíntota vertical, que
ocorre em x = -2.
lim
x →∞
1
= 0, r > 0
xr
e
lim
x →−∞
1
= 0, r > 0
xr
14
17
2. Assíntotas horizontais
limites no infinito
1. Assíntotas verticais e limites infinitos
Exemplo 5: Ache o limite: lim  5 − 22 
x →∞
x
Exemplo 4: Ache os limites
x 2 − 3x
lim
x →1−
x −1
e
e


2
2
1


lim  5 − 2  = lim 5 − lim 2 = lim 5 − 2 ⋅  lim 2  = 5 − 2 ⋅ 0 = 5
x →∞
x →∞ x
x →∞
x  x →∞

 x →∞ x 
x2 − 3x
lim
x →1+
x −1
Como o denominador é zero quando x = 1, mas o
Note que o gráfico tem
numerador não o é, decorre que o gráfico da
y = 5 como assíntota horizontal
à direita. Calculando o limite
de f(x) quando x → -∞, vê-se
que esta reta também é
assíntota
horizontal
à
esquerda.
função tem uma assíntota vertical em x = 1. Isto
implica que cada um dos limites dados é +∞ ou -∞.
lim
x →1−
x 2 − 3x
= +∞
x −1
e
lim
x →1+
x 2 − 3x
= −∞
x −1
15
18
3
2. Assíntotas horizontais
limites no infinito
e
2. Assíntotas horizontais
limites no infinito
e
Exemplo 6: Ache as assíntotas horizontais
dos gráficos das funções
Há uma forma fácil de determinar se o
gráfico de uma função racional tem assíntota
horizontal. Esse processo prático se baseia em
uma comparação dos graus do numerador e do
denominador da função racional.
a. y =
−2 x + 3
3x2 + 1
b. y =
−2 x 2 + 3
3x 2 + 1
c. y =
−2 x 3 + 3
3x 2 + 1
Como
o
grau
do
numerador é igual ao grau do
denominador,
a
reta
y = -2/3 é assíntota horizontal.
19
2. Assíntotas horizontais
limites no infinito
e
22
2. Assíntotas horizontais
limites no infinito
Assíntotas horizontais de funções racionais
e
Exemplo 6: Ache as assíntotas horizontais
dos gráficos das funções
Seja f(x) = p(x)/q(x) uma função racional.
1. Se o grau do numerador é inferior ao grau do denominador, então y = 0 é assíntota horizontal do gráfico de f
(à esquerda e à direita).
a. y =
−2 x + 3
3x2 + 1
2. Se o grau do numerador é igual ao grau do denominador,
então y = a/b é assíntota horizontal do gráfico de f
(à esquerda e à direita); a e b são os coeficientes dos
termos de maior grau de p(x) e q(x), respectivamente.
e
−2 x + 3
3x2 + 1
c. y =
−2 x 3 + 3
3x 2 + 1
23
3. Assíntotas inclinadas
Exemplo 6: Ache as assíntotas horizontais
dos gráficos das funções
a. y =
−2 x 2 + 3
3x 2 + 1
Como o grau do numerador é superior ao grau do
denominador, o gráfico não
tem assíntota horizontal.
3. Se o grau do numerador é superior ao grau do denominador, então o gráfico de f não tem assíntota
20
horizontal.
2. Assíntotas horizontais
limites no infinito
b. y =
b. y =
−2 x 2 + 3
3x 2 + 1
c. y =
Algumas curvas têm assíntotas que são
oblíquas, isto é, não são horizontais nem verticais.
Se
−2 x 3 + 3
3x 2 + 1
lim f ( x ) − ( mx + b )  = 0
x →∞
Como
o
grau
do
numerador é inferior ao grau
do denominador, y = 0 é
assíntota horizontal.
21
então a reta y = mx + b é chamada de
assíntota inclinada, pois a distância vertical entre
a curva y = f(x) e a reta y = mx + b tende a 0, como
na figura seguinte. (Uma situação análoga existe
quando fazemos x → -∞.)
24
4
3. Assíntotas inclinadas
3. Assíntotas inclinadas
Assim sendo
lim  f ( x ) − ( mx + b )  = 0
x →∞ 

x 
1



2

x
x 



lim  x − 2
− x  = lim  − 2
= lim  − 2x  = lim  − x

x →∞ 
x +1
 x →∞  x + 1 x →∞  x + 1  x →∞  1 + 1

x2

x 2 
quando x → ±∞


0
=− =0
1


Logo, a reta y = x é uma assíntota inclinada.
25
3. Assíntotas inclinadas
28
3. Assíntotas inclinadas
Para as funções racionais, as assíntotas
inclinadas ocorrem quando a diferença entre os
graus do numerador e do denominador é 1. Nesse
caso a equação da assíntota inclinada pode ser
encontrada por divisão de polinômios, como no
exemplo a seguir.
Derivada primeira:
f ′( x ) =
f ′( x ) =
(x
2
)
(x
+ 1 ⋅ 3x 2 − x 3 ⋅ 2x
2
)
+1
2
3 x 4 + 3 x 2 − 2x 4
(x
2
)
+1
2
=
=
3 x 4 + 3 x 2 − 2x 4
(x
x 4 + 3x2
(x
2
)
+1
2
=
2
)
+1
(
2
x2 x 2 + 3
(x
2
)
+1
)
2
Pontos críticos: x = 0
26
3. Assíntotas inclinadas
29
3. Assíntotas inclinadas
Exemplo 7: Ache a assíntota inclinada da
função
f (x) =
x
Derivada segunda:
f ′′( x ) =
3
2
) ⋅ ( 4x
2
+1
3
)
(
)
)
(
)
+ 6x − x 2 ⋅ x 2 + 3 ⋅ 2 ⋅ x 2 + 1 ⋅ 2x
(
)
(
)
( x + 1)
2 x ⋅ ( x + 1) ⋅ ( 2 x + 3 ) − 2 x ⋅ ( x + 3 ) 


f ′′( x ) =
( x + 1)
x2 + 1
x2 + 1
(x
f ′′( x ) =
A divisão de polinômios fornece:
(
(x
2
)
(
+ 1 ⋅ 2x ⋅ 2x 2 + 3 − 4 x 3 ⋅ x 2 + 3
3
2
2
)
x ⋅ x2 + 1
x3
x
x
f (x) = 2
=
− 2
=x− 2
x +1
x2 + 1
x +1
x +1
2
2
f ′′( x ) =
27
4
2
2
3
(
2
2 x ⋅  2 x 4 + 3 x 2 + 2 x 2 + 3 − 2 x 4 − 6 x 2 

 ⇒ f ′′( x ) = 2 x ⋅ 3 − x
3
3
2
2
x +1
x +1
(
)
(
)
)
30
5
3. Assíntotas inclinadas
Pontos de inflexão:
2x = 0 ⇒ x = 0
3 − x2 = 0 ⇒ x = ± 3
Os pontos de inflexão são:


3 3
3 3
 − 3; −
 , ( 0, 0 ) e  3;

4
4 



31
3. Assíntotas inclinadas
Intervalo
f(x)
( −∞, − 3 )
−3 3 4
x=− 3
(−
3, 0
)
x=0
0
(0, 3 )
x= 3
(
3, + ∞
3 3 4
)
f’(x)
f‘’(x)
Forma do
gráfico
+
+
Cresc.; CC
+
0
PI
+
-
Cresc.; CB
0
0
PI
+
+
Cresc.; CC
+
0
PI
+
-
Cresc.; CB
32
3. Assíntotas inclinadas
33
6