simulado - Rede La Salle

SIMULADO 1
1
Física
3
(Fuvest-SP)
No estádio do Morumbi, 120 000 torcedores assistem a
um jogo. Através de cada uma das 6 saídas disponíveis,
podem passar 1 000 pessoas por minuto. Qual é o tempo
mínimo necessário para esvaziar o estádio?
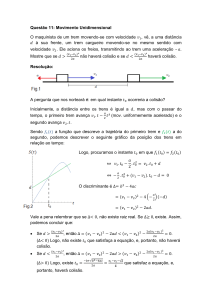
O esquema abaixo representa uma pista de corrida na
qual os competidores 1, 2 e 3, em um determinado instante, encontravam-se alinhados, na reta X, a 100 m da linha
de chegada Y. A partir dessa reta X, a velocidade de cada
um permaneceu constante. Quando o corredor 1 cruzou,
em primeiro lugar, a linha de chegada, os corredores 2 e
3 estavam, respectivamente, a 4 m e a 10 m dessa linha.
a) 1 hora
b)
1
hora
2
c)
1
de hora
4
(UERJ)
1
de hora
3
3
e)
de hora
4
d)
No instante em que o corredor 2 cruzar a linha de chegada Y, o corredor 3 estará a uma distância dessa linha,
em metros, igual a:
Resolução
Cada saída do estádio do Morumbi tem uma vazão de 1 000 torcedores por minuto. Se há 6 saídas no estádio, temos a vazão
de 6 000 torcedores por minuto.
Para determinar o tempo mínimo para esvaziar o estádio, pode-se fazer a seguinte regra de três:
6 000 torcedores  1 minuto
120 000 torcedores  x minutos
x = 20 minutos
Como 20 minutos equivalem a
a) 6,00
b) 6,25
c) 6,50
d) 6,75
Resolução
1
de hora, a alternativa correta
3
O competidor 1 corre os 100 m em um intervalo de tempo ∆t1;
já os competidores 2 e 3 correm, no mesmo intervalo de tempo,
96 m (100 − 4) e 90 m (100 − 10), respectivamente.
Assim, suas velocidades são dadas por:
é a d.
2
(UFPA)
Maria saiu de Mosqueiro às 6 horas e 30 minutos, de um
ponto da estrada onde o marco quilométrico indicava quilômetro 60. Ela chegou à Belém às 7 horas e 15 minutos, no
marco quilométrico da estrada que indicava quilômetro 0.
A velocidade média, em km/h, do carro de Maria, em sua
viagem de Mosqueiro até Belém, foi de:
v1 =
100
∆t1
v2 =
96
∆t 2
v3 =
90
∆t3
Como ∆t é o mesmo para todos, podemos encontrar a relação
entre as velocidades v2 e v3:
∆t 2 = ∆t3
a) 45
96 90
=
⇒ v 3 = 0, 9375 v 2
v2
v3
b) 55
Decorrido um novo intervalo de tempo, ∆tî, o competidor 2 cruza a linha de chegada. Nessa situação, o competidor 2 percorre
a distância de 4 m, e o competidor 3 percorre uma distância
menor, 10 − x, no mesmo intervalo de tempo ∆tî.
Como novamente ∆tî é comum a ambos, temos:
∆tî2 = ∆tî3
c) 60
d) 80
e) 120
Resolução
3
h. A distância per4
corrida foi de 60 km. Assim, a velocidade média desenvolvida
no percurso foi de:
4
10 − x
=
v2
v3
∆s 60
=
3
∆t
4
Vm = 80 ⇒ Vm = 80 km / h
⇒ x = 6, 25 m
Quando o competidor 2 cruza a linha de chegada, o competidor 3
encontra-se a 6,25 m dela.
A viagem de Maria durou 45 minutos ou
4
10 − x
=
⇒ 10 − x = 3,75 ⇒ x = 10 − 3,75 = 6, 25 ⇒
v2
0, 9375 v 2
Vm =
1
SIMULADO 1
4
Física
5
(Ufla-MG)
Um móvel se desloca em trajetória retilínea, sendo
S = 2 + 16t − 4t2 a sua equação horária. Se S é medido em
metros e t em segundos, podemos afirmar que:
a) o movimento é acelerado, sendo a aceleração igual a
8 m/s2.
(PUC-PR)
No instante em que a luz verde de um semáforo acende,
um veículo A, ali parado, parte com aceleração constante
de 2 m/s2. Um outro veículo B, que se movimenta na mesma direção e no mesmo sentido, só que com velocidade
constante de 10 m/s, passa por ele no exato momento
em que ele arranca.
Considerando os dados fornecidos pode-se afirmar que:
a) o veículo A ultrapassa o veículo B a 200 m do semáforo.
b) o movimento é uniformemente retardado até t = 2 s,
sendo a velocidade inicial igual a 16 m/s.
c) o móvel estava em repouso quando foram iniciadas as
observações.
b) o veículo A não alcança o veículo B.
d) o movimento é retardado com aceleração 8 m/s2 e posição inicial de 2 m.
c) os dois veículos seguem sempre juntos.
e) o movimento é uniformemente acelerado até o instante
2 s, sendo 8 m/s2 a aceleração e 16 m/s a velocidade
inicial.
e) o veículo A ultrapassa o veículo B a 100 m do semáforo.
d) o veículo A ultrapassa o veículo B a 40 m do semáforo.
Resolução
Resolução
Escrevendo as funções horárias das posições para cada veículo, temos:
1
sA = s0A + v0At + at2
2
1
⋅ 2 ⋅ t2 ⇒ sA = t2
sA =
2
1
sB = s0B + vBt + at2
2
sB = 10t
Para obter a posição de encontro, igualamos as funções horárias. Assim:
s A = sB
t2 = 10t
t(t − 10) = 0 ⇒ t = 0 s ou t = 10 s
Portanto, a posição de encontro é:
s = 10t
s = 10 ⋅ 10
s = 100 ⇒ s = 100 m
A aceleração do móvel é −8 m/s2, a velocidade inicial é 16 m/s
e a posição inicial é 2 m. Assim, o movimento é uniformemente
variado, progressivo e retardado (a função horária da posição é
uma função do 2.º grau), até o instante 2 s, quando a velocidade
é nula.
v = v0 + at
0 = 16 − 8t
t=2⇒t=2s
A partir desse instante, a velocidade torna-se negativa e o movimento passa a ser acelerado.
2
SIMULADO 1
6
Física
Considerando que os trechos AR e SB do gráfico II são
arcos de parábola, e o trecho RS é um segmento de reta,
os valores de SR e SS são, respectivamente:
a) 125 m e 775 m
(UFSM-RS)
Ao preparar um corredor para uma prova rápida, o treinador observa que o desempenho dele pode ser descrito,
de forma aproximada, pelo seguinte gráfico:
b) 200 m e 700 m
c) 225 m e 675 m
d) 250 m e 650 m
e) 300 m e 600 m
Resolução
Como a velocidade escalar média é vm = 54 km/h = 15 m/s, podemos determinar o intervalo de tempo total do trem do Metrô
entre as duas estações:
A velocidade média desse corredor, em m/s, é de:
a) 8,5
∆s
900
⇒ 15 =
⇒ ∆t = 60 ⇒ ∆t = 60 s
∆t
∆t
Como o intervalo de tempo é 60 s, as frações do intervalo de
tempo para a execução dos movimentos são: 20 s e 40 s.
Sabendo que o trem parte do repouso, para os primeiros 20
segundos de movimento uniformemente acelerado, podemos
escrever as funções horárias:
v = v0 + at
v = a ⋅ 20
v = 20a
1
s = s0 + v0t + at2
2
1
s = a ⋅ (20)2 ⇒ s = 200a ➀
2
Nos 20 segundos posteriores, durante o movimento uniforme,
os valores finais para a velocidade e a posição são:
v = 20a
sî = s0 + v0t
sî = 200a + 20a ⋅ 20 ⇒ sî = 600a ➁
Finalmente, para os 20 segundos finais de movimento uniformemente retardado, temos as velocidades e as posições finais
dadas por:
v = v0 + at
v = 20a − a ⋅ 20
v=0
1
sì = s0 + v0t + at2
2
1
sì = 600a + 20a ⋅ 20 − ⋅ a ⋅ (20)2
2
vm =
b) 10,0
c) 12,5
d) 15,0
e) 17,5
Resolução
O deslocamento do corredor equivale à área do trapézio. Assim:
∆s = A
(b + b 2 ) ⋅ h
∆s = 1
2
(10 + 6 ) ⋅ 12, 5
∆s =
2
∆s = 100
∆s 100
vm =
=
= 10 ⇒ v m = 10 m / s
∆t
10
7
(Mack-SP)
sì = 1 000a − 200a ⇒ sì = 800a
Como s = 900 m, temos que:
sì = 800a = 900
a = 1,125 m/s2
Entre duas determinadas estações de uma das linhas do
Metrô de São Paulo, o trem percorre o espaço de 900 m
no intervalo de tempo t, com velocidade escalar média de
54,0 km/h. O gráfico I representa a velocidade escalar do
trem nesse percurso, em função do tempo, e o gráfico II,
o espaço percorrido em função do tempo.
Substituindo em ➀, temos:
s = 200a
s = 200 ⋅ 1,125 = 225 ⇒ s = 225 m
Substituindo em ➁, temos:
sî = 600a
sî = 600 ⋅ 1,125 = 675 ⇒ sî = 675 m
3
SIMULADO 1
8
Física
9
(Ufla-MG)
Um veículo (A) vem trafegando por uma rua, quando,
inadvertidamente, um ciclista (B) entra nessa rua, a certa
distância à frente do veículo, no mesmo sentido e com
velocidade constante. Imediatamente, para evitar o choque, o motorista aciona os freios, de forma a desacelerar o
veículo uniformemente, até alcançar o ciclista sem tocá-lo,
o qual continua com sua velocidade constante. Considerando como instante inicial (t0 = 0) o instante em que o
motorista aciona o freio, o gráfico que melhor representa
o movimento do veículo (A) e do ciclista (B) é:
(UFPR)
Um trem de passageiros executa viagens entre algumas
estações. Durante uma dessas viagens, um passageiro
anotou a posição do trem e o instante de tempo correspondente e colocou os dados obtidos no gráfico abaixo:
a)
Com base no gráfico, considere as seguintes afirmativas:
I. Nessa viagem, o trem para em quatro estações diferentes.
II. O trem retorna à primeira estação após oito horas de
viagem.
III. O trem executa movimento uniforme entre as estações.
b)
IV. O módulo da velocidade do trem, durante a primeira hora
de viagem, é menor do que em qualquer outro trecho.
Assinale a alternativa correta.
a) Somente as afirmativas II e III são verdadeiras.
b) Somente as afirmativas I e II são verdadeiras.
c)
c) Somente as afirmativas I e III são verdadeiras.
d) Somente as afirmativas II e IV são verdadeiras.
e) Somente as afirmativas III e IV são verdadeiras.
Resolução
I.
d)
Errada. Considerando que a parada em uma estação ocorre
durante determinado intervalo de tempo, os trens têm duas
paradas. Os pontos de x = 0 não significam uma parada; o
trem pode estar passando pela origem das posições.
II. Correta. Ao final de oito horas de percurso, o trem passa por
duas estações e retorna à primeira estação.
III. Correta. O trem executa movimentos uniformes, pois sua posição varia linearmente com o tempo.
IV. Errada. Durante a primeira hora de viagem, o módulo da
velocidade do trem é maior que em qualquer outro trecho
(v = 200 km/h).
Resolução
O gráfico do ciclista (B), por executar um movimento uniforme
progressivo, deve ser uma reta crescente.
O gráfico do veículo (A), por executar um movimento uniformemente variado, progressivo e retardado, deve ser um arco de
parábola com concavidade voltada para baixo.
Essas duas curvas são mostradas corretamente no item a.
4
SIMULADO 1
Física
10 (UFF-RJ)
Resolução
Consideremos a queda livre de todos os corpos, independentemente e simultaneamente. Para o arranjo I, determinamos os
valores de T e Tî:
1
d
s2 = s0 + v 0 t + at 22 ⇒ 0 = d − 5t 22 ⇒ t 2 =
2
5
Em um dos seus projetos, o Grupo de Ensino do Instituto
de Física da UFF desenvolve atividades que permitam a
alunos com deficiências visuais terem experiências sensoriais diretas de fenômenos físicos.
Numa dessas atividades, objetos pesados são presos
a um barbante separados por distâncias bem definidas.
Inicialmente, o conjunto é mantido na vertical, segurando-se o objeto mais alto e mantendo-se o mais baixo no
chão. Em seguida, o conjunto é solto, permitindo que o
aluno ouça os sons emitidos ao fim da queda de cada
objeto. Dois destes arranjos, chamados I e II, são mostrados na figura abaixo.
s3 = s0 + v 0 t +
s 4 = s0 + v 0 t +
1 2
at ⇒ 0 = 4d − 5t32 ⇒ t3 =
2 3
4d
d
=2
5
5
1 2
7d
=
at ⇒ 0 = 7d − 5t 24 ⇒ t 4 =
2 4
5
7⋅
d
d
 2, 64
5
5
Assim, determinamos T e Tî pela diferença dos tempos:
T = t3 − t 2 =
d
5
Tî = t4 − t3 = 0,64
d
5
d > 0,64 d .
5
5
Realizando o mesmo procedimento para o arranjo II, temos:
Ou seja: T > Tî, pois
s 2 = s0 + v 0 t +
1 2
at ⇒ 0 = d − 5t 22 ⇒ t 2 =
2 2
s3 = s0 + v 0 t +
1 2
at ⇒ 0 = 4d − 5t32 ⇒ t3 =
2 3
s 4 = s0 + v 0 t +
1 2
at ⇒ 0 = 9d − 5t 42 ⇒
2 4
d
5
4d
d
=2
5
5
9d
d
=3
5
5
Assim, determinamos T e Tî pela diferença dos tempos:
T = t3 − t 2 =
d
5
d
5
Ou seja: T = Tî.
Tî = t4 − t3 =
Em ambos os arranjos as distâncias entre os objetos 1 e 2
e 2 e 3 são, respectivamente, iguais a d e 3d. No arranjo I a
distância entre os objetos 3 e 4 é 3d, enquanto no arranjo
II a distância entre eles é 5d.
Escolha a alternativa que exibe corretamente a relação
entre os intervalos de tempo decorridos entre os sons
emitidos pela chegada ao chão dos objetos 2 e 3 (T) e
3 e 4 (Tî) nos 2 arranjos.
arranjo I
arranjo II
a) T , Tî
T = Tî
b) T = Tî
T , Tî
c) T = Tî
T . Tî
d) T . Tî
T , Tî
e) T . Tî
T = Tî
5