Aula 1: Definição de Fluído, Objetivos da Mecânica dos Fluídos

Exercícios Segunda Prova FTR
g=9,81 m/s2=32,2 ft/s2
ρH2O=999 kg/m3=1,94 slug/ft3
Dados gerais:
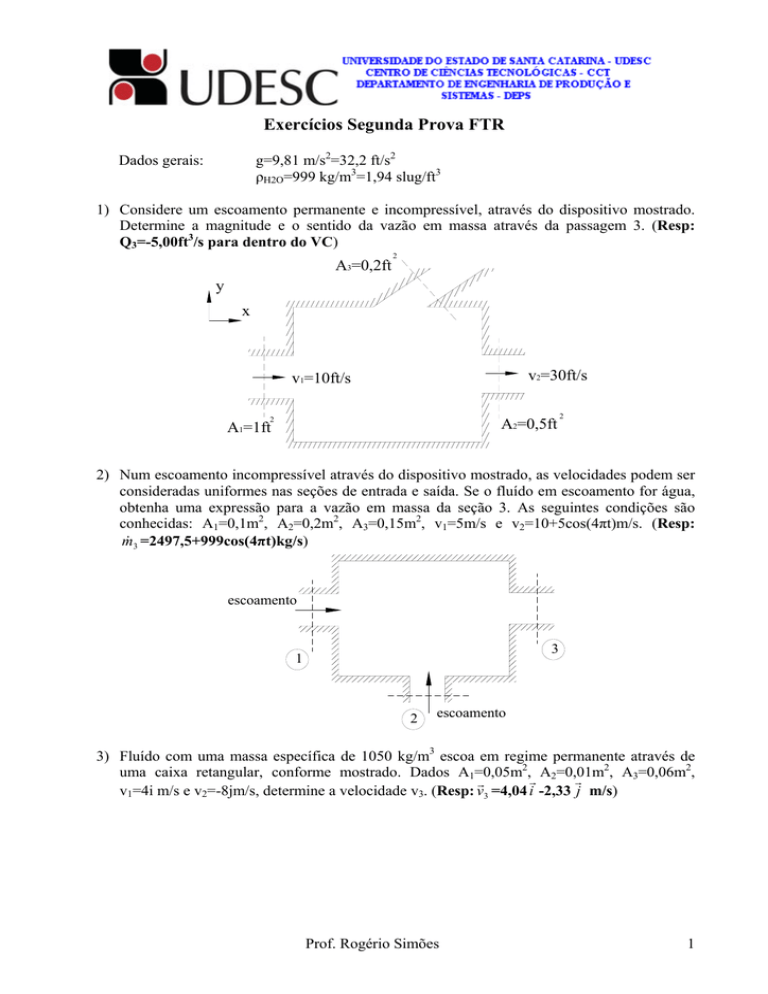
1) Considere um escoamento permanente e incompressível, através do dispositivo mostrado.
Determine a magnitude e o sentido da vazão em massa através da passagem 3. (Resp:
Q3=-5,00ft3/s para dentro do VC)
A3=0,2ft
2
y
x
v2=30ft/s
v1=10ft/s
2
A2=0,5ft
A1=1ft
2
2) Num escoamento incompressível através do dispositivo mostrado, as velocidades podem ser
consideradas uniformes nas seções de entrada e saída. Se o fluído em escoamento for água,
obtenha uma expressão para a vazão em massa da seção 3. As seguintes condições são
conhecidas: A1=0,1m2, A2=0,2m2, A3=0,15m2, v1=5m/s e v2=10+5cos(4πt)m/s. (Resp:
m& 3 =2497,5+999cos(4πt)kg/s)
escoamento
3
1
2
escoamento
3) Fluído com uma massa específica de 1050 kg/m3 escoa em regime permanente através de
2
uma caixa retangular, conforme mostrado. Dados A1=0,05m2,r A2=0,01m
, A3=0,06m2,
r
r
v1=4i m/s e v2=-8jm/s, determine a velocidade v3. (Resp: v3 =4,04 i -2,33 j m/s)
Prof. Rogério Simões
1
A2
x
A3
A1
60°
4) Fluído incompressível escoa através do dispositivo mostrado. Na entrada, o escoamento é
uniforme com velocidade v1=2,0 ft/s. O perfil de saída é linear, v2=ky. O dispositivo tem
largura w=1,25 ft. Determine k, considerando o escoamento permanente. (Resp: k=14,55s-1)
y
x
h=0,275 ft
60°
5) Água entra num tubo bidimensional de largura constante, h, com velocidade uniforme, U. O
tubo faz uma curva de 90° que distorce o escoamento, de modo a produzir o perfil de
velocidade linear mostrado na saída, com vmax=2vmin. Avalie vmin, se U=7,5m/s. (Resp:
vmin=5m/s)
y
vmax
vmin
v=vmin[2 -x/h]
U
h
x
6) Considere um escoamento de água através do dispositivo mostrado. Sabendo que a seção 1 é
circular de diâmetro 7in, as seções 2 e 3 são quadradas de dimensões 4in e 5in
respectivamente. A seção 1 possui uma distribuição de velocidades na forma de um

r2 
parabolóide de equação: v1 = v1 max 1 − 2  , a seção 2 possui distribuição linear de

R1 

velocidades como apresentado na figura e a seção 3 a velocidade é uniforme ao longo da
Prof. Rogério Simões
2
seção. Dados v1max=12ft/s e v2max=15ft/s, determine as componentes de v3 em relação ao
sistema de coordenadas apresentado. Apresente as hipóteses necessárias para a solução do
problema.
v3
y
3
x
v1max=12ft/s
v2max=15ft/s
2
1
7) Um jato de água sai de uma tubulação a uma velocidade constante média de 6m/s, choca-se
com uma placa plana, que está em repouso e orientada normalmente a direção do jato. A
seção da área de saída da tubulação tem 7cm2. Qual é a força horizontal total que os fluídos
em contato com a placa exercem sobre ela? (Resp: F=-2,57 kgf)
8) Um jato de água de vazão Q0 e velocidade v0, incide sobre uma placa e é defletido conforme
a figura. Se a placa está parada, calcule as componentes Fx e Fy da força devido ao jato
sobre a placa. Faça as hipóteses necessárias para a resolução do problema. (Resp:
Fx=-0,9ρv0Q0, Fy=31/2 ρv0Q0/10)
Q1=0,6 Q
0
Q
v
60°
0
0
Q2
9) Um grande tanque está fixo a um carrinho, como mostrado. Água jorra do tanque através de
um bocal de 600 mm2 a uma velocidade de 10m/s. O nível da água no tanque é mantido
constante, por adição, mediante um tubo vertical. Determine a tração no cabo que mantém o
carrinho estacionário. (Resp: 59,94N)
Prof. Rogério Simões
3
v
10) Um jato de gasolina (DR=0,8) com seção de 0,08m2 e velocidade v0=50m/s, incide sobre
uma placa e é defletido conforme a figura, mantendo o valor das velocidades em ambas as
direções. Se a placa está em movimento contrário ao fluxo de gasolina com velocidade de
v=15m/s, calcule as componentes Fx e Fy da força devido ao jato sobre a placa. Faça as
hipóteses necessárias para a resolução do problema.
Q1=0,7 Q
0
50°
y
x
v
0
v
Q2
11) Um jato de água que sai de um bocal estacionário a 15m/s (A=0,05m2) atinge uma aleta
curva montada num carrinho, conforme mostrado. A aleta desvia o jato de um ângulo θ=50°.
Determine o valor de M, necessário para manter o carrinho estacionário. (Resp:
M=409,24kg)
v
=50°
M
12) Um jato de água de vazão Q0=3m3/s e velocidade v0=15m/s, incide sobre uma placa e é
defletido conforme a figura. Se a placa está parada, calcule as componentes Fx e Fy da força
devido ao jato sobre a placa. Faça as hipóteses necessárias para a resolução do problema.
(Resp.: FRx=-40459,5N , FRy=7786,4N)
Prof. Rogério Simões
4
Q1=0,6 Q
0
Q
v
60°
0
0
Q2
13) Um prato raso e circular tem um orifício de bordas vivas no seu centro. Um jato d’água, de
velocidade V, atinge o prato concentricamente. Obtenha uma expressão para a força externa
necessária a fim de manter o prato no lugar, se o jato que sai pelo orifício também
r tem
velocidade V. Avalie a força para V=5m/s, D=100mm e d=20mm. (Resp: F=-321,5 i N)
14) Um jato de água é dirigido contra uma aleta, que poderia ser uma pá de turbina ou de
qualquer outra máquina hidráulica. A água sai do bocal estacionário, de 50 mm de
diâmetro, com uma velocidade de 20m/s e entra na aleta tangente a superfície, em A. A
superfície interna da aleta, em B, faz um ângulo θ=150° com o sentido do x. Calcule a força
que deve
para manter a velocidade da aleta constante em U=5m/s. (Resp.: F=r ser aplicada
r
823,56 i +220,67 j N)
15) Água proveniente de um bocal estacionário atinge uma aleta móvel com curvatura de θ
=120°. A aleta move-se com velocidade constante, afastando-se do bocal, com velocidade
U=30ft/s, e recebe um jato que sai do bocal com velocidade V=100ft/s. O bocal tem uma
Prof. Rogério Simões
5
área de saída de 0,04ft2. Determine a rforça que rdeve ser aplicada para manter a velocidade
da aleta constante. (Resp.: F=-570,36 i +329,30 j lbf)
16) Um jato d’água saindo de um bocal estacionário, encontra uma aleta com curvatura θ=90°
que se move afastando-se do bocal a uma velocidade constante de 15m/s. O jato tem área de
seção de 600 mm2 a uma velocidade de 30m/s. Determine a força querdeve ser aplicada para
r
manter a velocidade da aleta constante. (Resp.: F=-134,87 i +134,87 j N)
17) Um jato de óleo (DR=0,8) atinge uma aleta que altera a direção do fluído de θ=180°. A área
do jato é 1200 mm2 e sua velocidade relativa ao bocal estacionário é 20m/s. A aleta move-se
aproximando do bocal a 10m/s. Determine a força
que deve ser aplicada para manter a
r
velocidade da aleta constante. (Resp.: F=-1,726 i kN)
18) O disco circular, cuja seção reta é mostrada, tem um diâmetro externo de 0,15m. Um jato
d’água o atinge concentricamente e em seguida flui para fora, ao longo da superfície do
disco. A velocidade do jato é 45m/s e o disco move-se para a esquerda a 10m/s. Determine a
espessura da lâmina d’água no raio de 75mm a partir do eixo do jato. Que
força horizontal é
r
necessária para manter esse movimento? (Resp.: t=4,17mm, F=4243,6 i N)
Prof. Rogério Simões
6
19) Um duto com área de 5ft2 se contrai gradualmente para uma área de 2,5ft2 conforme a figura
abaixo. A queda de pressão entre as duas seções é medida com um manômetro de mercúrio
com deflexão de h=20in. Calcule a vazão através do duto. (Resp: Q=106,16ft3/s)
20) A água que flui através de um grande reservatório aberto, conforme indicado na figura
abaixo, descarrega-se horizontalmente na atmosfera. Calcule a velocidade v3 e a velocidade
v2. (Resp: v2=16,05ft/s, v3=4,01ft/s)
21) Uma tubulação inclinada de diâmetro igual a 6in é ligada por meio de um redutor a um tubo
de diâmetro igual a 4in. A água se escoa através do tubo, conforme indicado a figura abaixo.
Calcule a velocidade média v2. (Resp: v2=31,8ft/s)
Prof. Rogério Simões
7
22) Um bocal de 2in de diâmetro é instalado na extremidade de um tubo de 6in de diâmetro. Se
a pressão no tubo for de 20psig, calcule a descarga da água em pés por segundo. (Resp:
v=54,83ft/s)
23) Um sifão de 1in de diâmetro é usado para drenar gasolina (DR=0,75) de um grande tanque,
conforme ilustrado na figura abaixo. O ponto mais elevado do sifão está situado a 4ft acima
da superfície da gasolina e o sifão descarrega num ponto a 9ft abaixo da superfície. Calcule
a vazão em ft3/s e a pressão no ponto mais elevado do sifão. (Resp: Q=0,131ft3/s, p2=4,23psig)
24) Uma vazão de 5ft3/s de água escoa sem atrito através da expansão indicada na figura abaixo.
A pressão na seção 1 é igual a 12psig. Suponha escoamento unidimensional. Encontre a
pressão em 2. (Resp: p2=12,22psig)
Prof. Rogério Simões
8