Estados de Tensão

1
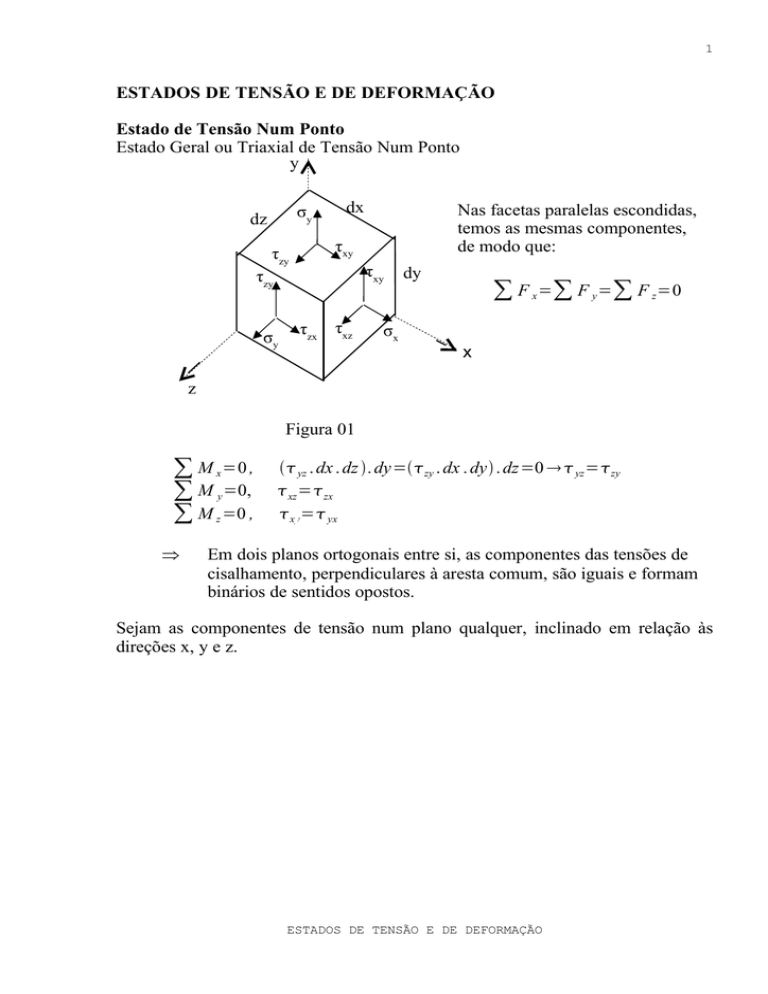
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
Estado de Tensão Num Ponto
Estado Geral ou Triaxial de Tensão Num Ponto
y
σy
dz
dx
τxy
τzy
τxy
τzy
σy
Nas facetas paralelas escondidas,
temos as mesmas componentes,
de modo que:
τzx
τxz
σx
dy
∑ F x =∑ F y =∑ F z=0
x
z
Figura 01
∑ M x =0 ,
∑ M y =0,
∑ M z =0 ,
⇒
 yz . dx . dz . dy=zy . dx . dy . dz=0   yz =zy
xz =zx
xy = yx
Em dois planos ortogonais entre si, as componentes das tensões de
cisalhamento, perpendiculares à aresta comum, são iguais e formam
binários de sentidos opostos.
Sejam as componentes de tensão num plano qualquer, inclinado em relação às
direções x, y e z.
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
2
y
dAz
dAx
dA: área do triângulo inclinado
x
dAx
Figura 02
z
Componentes de tensão num plano qualquer:
y
ρy
ρx
ρz
x
z
Figura 03
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
3
Componentes da tensão nos planos ⊥ a x, y e z:
y
τxz
σx
σz
τzx
τzy
τxy
τyz
τyx
x
σy
z
Figura 04
Equilíbrio de Forças:
∑ F x =0 ,
∑ F y =0 ,
∑ F z=0 ,
x . dA= x . dA x  xy . dA y  zx . dAz
 y . dA=xy . dA x  y . dA y zy . dA z
 z . dA= xz . dA x yz . dA y  z . dAz
ou, matricialmente,
[ ][
][ ]
x
 x  yz zx dA x
dA⋅  y =  xy  y zy ⋅ dA y
z
xz  yz  z dA z
Obs.: A matriz das componentes da tensão nos planos perpendiculares a x, y e z é
simétrica (τxy = τyx, τyz = τzy, τzx = τxz)
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
4
Escrevendo
dAx = nx.dA,
dAy = ny.dA e dAz = nz.dA,
onde nx, ny e nz são os cossenos diretores da normal n ao plano inclinado,
relativos às direções x, y e z, respectivamente, temos:
[ ][
][ ]
x
 x  yz zx n x
 y = xy  y zy ⋅ n y
z
xz  yz  z n z
⇒
O estado de tensão num ponto fica determinado pelas seis
componentes σx, σy, σz, τxy = τyx, τyz = τzy, τzx = τxz, medidas em três planos
ortogonais entre si, que contenham o ponto. As componentes em qualquer outro
plano são obtidas a partir dessas seis componentes.
A tensão resultante no plano inclinado é
=  2x  2y 2z
e pode ser decomposta numa componente normal σ e outra tangencial τ, tais que
=   22
com
 = x . n x  y . n y  z . n z
ou
 = x . n 2x  y . n 2y  z . n 2z 2.  xy . n x . n y 2 . yz . n y . n z 2. zx . n z . n x
Considerando que nx, ny e nz são as variáveis em questão (cada conjunto nx, ny, nz
define um plano que contem o ponto), a expressão acima é a equação de uma
superfície central de 2a ordem. Assim sendo, girando-se o sistema de coordenadas
(nx, ny, nz), pode-se obter uma equação onde são nulos os coeficientes dos
produtos de coordenadas.
Se assim o fizermos, teremos
 = 1 . n12 2 . n 22 3 . n32
e
12=23=31 =0 ,
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
5
onde as novas direções 1, 2 e 3 são chamadas de direções principais.
Os planos normais a estas direções são os chamados planos principais e as tensões
normais σ1, σ2 e σ3 são as tensões principais. Designa-se σ1 ≥ σ2 ≥ σ3.
σ2
σ1
σ3
Figura 05
Tomando como referência as direções principais, as componentes da tensão num
plano qualquer seriam:
][ ]
[] [
1
 1 0 0 n1
2 = 0  2 0 ⋅ n2
3
0 0  3 n3
{
1= 1 . n1
 2= 2 . n 2
3= 3 . n3
ou
}
Como n 2x n 2y n 2z =n 21n 22n32=1 , temos:
2
2
   
2
1


 2  3 =1
1
2
3
Interpretando as componentes ρ1, ρ2 e ρ3 como um conjunto de variáveis, a
expressão acima representa um elipsóide cujos semi-eixos são as tensões
principais σ1, σ2 e σ3. É o chamado elipsóide das tensões.
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
6
2
σ2
ρ
σ1
σ3
3
1
=  212223
Figura 06
Daí se conclui que σ1 = σmáx e que σ3 = σmin (não há coordenada da superfície do
elipsóide maior do que σ1 nem menor do que σ3).
Determinação das Tensões Principais:
Suponhamos que o plano inclinado é um plano principal.
y
n
ρ=σ
(τ = 0)
x
z
Figura 07
Assim,
 x = . n x ,
[ ][
 y = . n y ,
][ ]
 x  yx  yz n x
nx
 .⋅ n y = xy  y xy ⋅ n y
nz
 xz  yz  z n z
 z = . n z
e
ou
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
7
[
][ ] [ ]
 x −
 yx
 yz
nx
0
⋅
=
xy
 y −
xy
ny 0
0
 xz
 yz
 z − n z
(sitema homogêneo)
A solução trivial nx = ny = nz = 0 contraria a hipótese nx2 + ny2 + nz2 = 1.
Para que um sistema homogêneo tenha solução não trivial é necessário que o
determinante da matriz do sistema seja nulo, isto é,
∣
 x −
 xy
xz
∣
 yx
 yz
 y −
 xy =0
 yz
 z −
Desenvolvendo este determinante, temos a equação do terceiro grau:
 3− I 1 .  2 I 2 . −I 3=0
onde
I 1= x  y  z
I 2= x .  y  y ,  z  z .  x −2xy −2yz −2zx
∣
∣
 x  yx  yz
I 3=  xy  y  xy
 xz  yz  z
As raízes desta equação são:
I

 1= 1 2⋅cos ⋅ Q
3
3
I

 1= 1 2⋅cos 240 0 ⋅ Q
3
3
I

 1= 1 2⋅cos 1200 ⋅ Q
3
3

 
 
 
R
Q 3
 I 21 −3. I 2 
Q=
9
−9. I 1 . I 227 . I 32 . I 31 
R=
54
onde, =arc cos
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
8
Como os valores das tensões principais σ1, σ2 e σ3 independem das direções x, y e
z previamente estabelecidas, os coeficientes I1, I2 e I3 também independem destas
direções e, por isto, são chamados de Invariantes de Tensão ou Invariantes do
Estado de Tensão.
Casos Particulares:
a) Se I3 = 0, uma das soluções é nula
⇒ Estado Plano ou Biaxial de Tensão
b) Se I2 = I3 = 0, duas soluções são nulas ⇒ Estado Simples ou Uniaxial de
Tensão
Para determinarmos os planos principais basta substituir cada um dos valores de σ
(σ1, σ2, σ3) no sistema homogêneo e determinar, em cada caso, os cossenos
diretores da normal ao plano (nx, ny e nz).
Porém, como as equações de um sistema homogêneo são linearmente
dependentes, teremos, em cada caso, infinitas soluções do tipo
[] []
nx
n x0
n y =⋅ n y0
nz
n z0
onde β é um escalar diferente de zero e nxo, nyo e nzo valores numéricos
conhecidos, obtidos na resolução do sistema.
A solução única, para cada plano principal, é obtida da condição n 2x n 2y n2z =1 ,
isto é,
[] [ ]
nx
n
1 x0
n y = ⋅ n y0
n
nz
n z0
onde
n=  n 2x0 n2y0n 2z0
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
.
9
Círculos de Mohr:
Em muitos casos práticos, um dos planos principais é reconhecido por simples
observação (casos das solicitações simples, por exemplo). Nestes casos, a
determinação dos demais planos principais e das tensões principais se simplifica.
Seja determinar as componentes de tensão normal σ e de cisalhamento τ num
plano qualquer paralelo a uma das três direções principais (por exemplo, à direção
3).
n
dz
σ2
σ
σ1
θ
dS
dy θ
dS . cos θ
σ3
dx
σ1
σ2
Figura 08
∑ F n=0
,
⋅dS= 1⋅dS⋅cos ⋅cos  2⋅dS⋅sen ⋅sen 
 = 1 cos2  2⋅sen2 
∑ F t =0
,
⋅dS = 1⋅dS⋅cos ⋅sen − 2⋅sen ⋅cos 
= 1− 2 ⋅sen ⋅cos 
A primeira expressão pode ser escrita na forma, lembrando que
1cos 2 
1−cos 2
2
2
e sen =
,
cos =
2
2
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
t
dS . sen θ
10
1cos 2
1−cos 2 
= 1⋅
 2⋅
2
2
=
 1 2  1− 2

⋅cos 2
2
2
A segunda expressão pode ser escrita na forma
=
 1− 2
⋅sen 2
2
Estas expressões fornecem os valores das componentes de tensão normal e de
cisalhamento nos planos paralelos ao eixo principal 3. De maneira análoga,
podemos expressar as componentes de tensão nos planos paralelos aos demais
eixos principais.
As expressões acima são, na verdade, as equações paramétricas de uma
circunferência
x=ar⋅cos 
y=br⋅sen 
onde
é a tensão normal
é a tensão de cisalhamento
x=
y=

 1 2
,0
2
 − 2
r= 1
3
=2
a , b=

são as coordenadas do centro do círculo
é o raio do círculo
é o parâmetro (θ é o ângulo entre o plano
principal 1 e o plano qualquer)
Elevando ao quadrado cada membro de cada equação e somando membro a
membro, obtemos:
[
2
]
[
  2
 − 2
− 1
2= 1
2
2
2
]
ou
 x−a2 y−b2=r 2
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
11
que é a equação normal da circunferência.
τ
σ
(σ,τ)
r
τ
2θ
r=
 1− 2
2
σ2
 1 2
2
σ1
Figura 09
Cada ponto da circunferência representa um plano inclinado de um ângulo θ em
relação ao plano principal 1, onde atuam componentes de tensão σ e τ iguais às
suas coordenadas.
Analogamente, teremos mais dois círculos semelhantes a este: um, cuja
circunferência representa os planos paralelos à direção principal 2 e outro, cuja
circunferência representa os planos paralelos à direção principal 1.
τ
τmáx
2θ = 90°
σ3
σ2
σ1
Figura 10
A estes círculos dá-se o nome de Círculos de Mohr.
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
σ
12
Pode-se demonstrar que os planos de inclinação arbitrária em relação aos eixos
principais são representados pelos pontos da região hachurada da figura acima.
Assim sendo, a máxima tensão de cisalhamento num ponto qualquer de um corpo
solicitado vale
máx =
 1− 3
 − min
= máx
2
2
e age num plano paralelo à direção principal 2 (direção da tensão principal
intermediária σ2), inclinado de 45o em relação aos planos principais 1 e 3
(respectivamente, os planos onde agem as máxima e mínima tensões normais σ1 e
σ3).
Como podemos observar, pontos diametralmente opostos da circunferência,
representam planos ortogonais entre si.
Assim, podemos construir o Círculo de Mohr a partir das componentes de tensão
em dois planos quaisquer ortogonais entre si, paralelos a uma direção principal.
y
σy
τyx
τxy
x
z
σz
σx
Figura 11
Adotando-se a seguinte convenção de sinais para as tensões de cisalhamento,
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
13
τ
τ
τ
τ
(-)
(+)
o Círculo de Mohr fica
τ
σI
σx
σy
σII
τyx
2θ
(σx + σy)/2
τxy
(σx - σy)/2
FIGURA 12
Centro do Círculo:
Raio do Círculo:

 x  y
,0
2
r=


2

 x − y
2xy
2
As tensões principais são, portanto, σz, σI e σII, onde
  y
 I , II = x
±
2


2
 x − y
2xy
2
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
σ
∣ xy∣=∣ yx∣
14
Os planos principais são o plano perpendicular ao eixo z e os planos paralelos a z
dados por:
 xy
2⋅ xy
tg 2 P =−
ou
tg
2

=−
 x − y
P
 x− y
2
Casos Particulares:
a) Estado Plano de Tensão:
τ
τmáx = σ1 / 2
2θ = 90°
σ
σ3 = 0
σ2
σ1
b) Estado Simples de Tensão:
Figura 13
τ
τmáx = σ1 / 2
2θ = 90°
σ
σ2 = σ3 = 0
σ1
Figura 14
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
15
c) Estado Triaxial Uniforme de Tensão:
τ
σ
σ1 = σ2 = σ3
Figura 15
Estado de Deformação Num Ponto
y
v
w
z
A
A’
u
x
Figura 16
AA’: deslocamento do ponto genérico A
(u,v,w): componentes de vetor-deslocamento AA’ segundo os eixos x, y e z,
respectivamente
As deformações lineares do ponto segundo as direções x, y e z são,
respectivamente:
εx = ∂u / ∂x, εy = ∂v / ∂y e εz = ∂w / ∂z.
As deformações angulares segundo os planos xy, yz e zx são, respectivamente:
γxy = ∂u / ∂y + ∂v / ∂x, γyz = ∂v / ∂z + ∂w / ∂y e γzx = ∂w / ∂x + ∂u / ∂z.
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
16
Estas componentes da deformação (deformações lineares e angulares) constituem
o Estado de Deformação do Ponto, isto é, são suficientes para se determinar as
componentes em quaisquer outras direções.
De fato, seja determinar as componentes da deformação segundo as direções
arbitrárias x’, y’ e z’, tais que
nxx, nxy e nxz sejam os cossenos diretores de x’ em relação a x, y e z,
respectivamente,
nyx, nyy e nyz sejam os cossenos diretores de y’ em relação a x, y e z,
respectivamente,
nzx, nzy e nzz sejam os cossenos diretores de z’ em relação a x, y e z,
respectivamente.
Assim, podemos escrever
x = nxx.x’ + nyx.y’ + nzx.z’
y = nxy.x’ + nyy.y’ + nzy.z’
z = nxz.x’ + nyz.y’ + nzz.z’
x’ = nxx.x + nxy.y + nxz.z
y’ = nyx.x + nyy.y + nyz.z
z’ = nzx.x + nzy.y + nzz.z
ou
As variações das componentes do deslocamento, u, v e w, são:
∂u
∂u
∂u
⋅dx ⋅dy ⋅dz
∂x
∂y
∂z
∂v
∂v
∂v
dv= ⋅dx ⋅dy ⋅dz
∂x
∂y
∂z
∂w
∂w
∂w
dw=
⋅dx
⋅dy
⋅dz
∂x
∂y
∂z
du=
ou, matricialmente,
[ ][ ]
∂u
∂x
du
∂v
dv =
∂x
dw
∂w
∂x
[]
∂u
∂y
∂v
∂y
∂w
∂y
∂u
∂u
∂z
∂x
dx
∂v
∂v
⋅ dy =
∂z
∂x
dz
∂w
∂w
∂z
∂x
[]
∂u
∂y
∂v
∂y
∂w
∂y
∂u
∂z n
n yx n zx dx '
xx
∂v
⋅ n xy n yy n zy ⋅ dy '
∂z
dz '
∂ w n xz n yz n zz
∂z
[
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
][ ]
17
A variação da componente u, por exemplo, segundo o novo sistema de eixos é:
du’ = nxx.du + nxy.dv + nxz.dw.
Se substituirmos, nesta expressão, os valores de du, dv e dw acima indicados ,
poderemos deduzir que:
x ' =
∂u'
=n 2xx . x n 2xy . y n 2xz .  z n xx . n xy .  xy n xy . n xz .  yz n xz . n xx .  zx
∂ x'
que é a equação de uma superfície central de 2a ordem análoga à obtida no estudo
do estado de tensão. A comparação entre as duas equações estabelece as seguintes
correspondências:
εx ↔ σx, εy ↔ σy, εz ↔ σz, γxy ↔ 2τxy, γyz ↔ 2τyz, γzx ↔ 2τzx.
Esta expressão dá o valor da deformação linear numa direção qualquer, enquanto
a obtida anteriormente dava o valor da tensão normal também numa direção
qualquer.
Daí, podemos afirmar que todo o estudo feito para o estado de tensão é válido
para o estado de deformação, se respeitarmos as correspondências acima.
Desta forma, existem três direções ortogonais entre si, segundo as quais as
deformações angulares são nulas. São as direções principais, designadas por 1, 2 e
3. Os planos normais a estas direções são os chamados planos principais e as
deformações lineares segundo estas direções, ε1 ≥ ε2 ≥ ε3, são as deformações
principais.
Tais deformações podem ser obtidas, a exemplo do estado de tensão, pelas
soluções da equação
ε3 - I1.ε2 + I2.ε - I3 = 0
onde, I 1= x  y z
 2xy  2yz 2zx
I 2=x . y  y . z  z .  x −
− −
4
4
4
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
18
∣ ∣
x
I 3=
 xy
2
 xz
2
 yx
2
y
 yz
2
 yz
2
 xy
2
z
são os Invariantes de Deformação ou Invariantes do Estado de
Deformação.
Casos Particulares:
a) Se I3 = 0, uma das soluções é nula
⇒
b) Se I2 = I3 = 0, duas soluções são nulas
⇒
Estado Plano ou Biaxial de
Deformação
Estado Simples ou Uniaxial de
Deformação
Os planos principais são obtidos de maneira análoga à do estado de tensão.
Os Círculos de Mohr também podem ser construídos analogamente aos do estado
de tensão, lembrando que, no eixo horizontal marcamos as deformações lineares ε
e no vertical, a metade das deformações angulares γ.
γ/2
γmáx/2 = (ε1 – ε3) /2
90°
ε3
ε2
ε1
Figura 17
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
19
Supondo, por exemplo, a direção z principal, as deformações principais, normais
aos planos paralelos à essa direção z, são
 
I , II = x y ±
2

2
  
x − y

 xy
2
2
2
Os planos principais são o plano perpendicular ao eixo z e os planos paralelos a z
dados por:

tg 2 P =− xy
 x − y
Lei de Hooke Generalizada
Estado Geral ou Triaxial de Tensão Num Ponto
y
dx
dz
σy
τyz
τyx
τxy dy
τzy
σz
τzx
τxz
σx
x
z
Figura 18
Sendo εij a deformação linear na direção i provocada pela tensão normal σj, temos:
a) deformações devidas a σx:
xx =
x
,
E
 yx = zx =−⋅ xx =−
⋅ x
E
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
20
b) deformações devidas a σy:
 yy =
y
,
E
 xy =zy =−⋅ yy=−
⋅ y
E
c) deformações devidas a σz:
zz =
z
,
E
xz = yz =−⋅ zz =−
⋅ z
E
d) deformações devidas a γxy, γyz e γzx:
 xy =
 xy
,
G
 xz =
xz
G
e
 yz =
 yz
G
Superpondo os efeitos, temos:
x 
− ⋅ y  z 
E E
 
 y = y − ⋅ z  x 
E E
 
z = z − ⋅ x  x 
E E


 xy = xy ,  yz = yz e
G
G
x =
 zx =
 zx
G
onde G=
E
2⋅1
As expressões acima representam a Lei de Hooke Generalizada, isto é, para o
Estado Geral de Tensão.
Observa-se que se os eixos principais do estado de tensões são exatamente os
mesmos eixos principais para o estado de deformações.
Se no plano xy tem-se um estado plano de tensões, as deformações neste memo
plano se comportarão como em um estado plano de deformações porém a

deformação principal z =− ⋅ x  x  será, em geral, diferente de zero.
E
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
21
Nos planos principais, as deformações são:
1 
− ⋅ 2 3
E E
 
2= 2 − ⋅ 3 1 
E E
 
3= 3 − ⋅ 1 2
E E
 12 = 23 =31 =0
1 =
A deformação volumétrica no ponto é dada por:
v =
V V f −V i
=
V
Vi
dz+εz.dz
dy+εy.dy
dy
dx
onde
dz
dx+εx.dx
V i =dx⋅dy⋅dz
V f =dx⋅dy⋅dz⋅1x ⋅1 y ⋅1 z 
v =1x ⋅1 y ⋅1z −1=1 x  y z x⋅ y  x⋅z  y⋅ z  x⋅ y⋅ z −1
Devido à hipótese das pequenas deformações, os produtos de deformações são
valores desprezíveis na presença das deformações. Assim, a deformação
volumétrica pode ser escrita, de forma aproximada, como
v = x  y z = I 1=123
ou, devido à Lei de Hooke,
1−2⋅
v = x  y  z ⋅
E
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
22
Observação:Para o Estado Triaxial Uniforme, σx = σy = σz = σ, temos:
onde
1−2⋅
e
x = y = z =⋅
E
3⋅1−2⋅

v =
⋅=
E
K
E
K=
é o Módulo de Deformação Volumétrica
3⋅1−2⋅
do Material
Se σ ≥ 0, então εv ≥ 0 e se σ ≤ 0, então εv ≤ 0. Isto implica em dizer
que 1 - 2ν ≥ 0 → ν ≤ 0,5. Este valor é um limite para o coeficiente de
Poisson, isto é, não há material com este coeficiente maior do que
0,5.
Medidas de deformações planas - rosetas
As deformações lineares em um ponto podem ser medidas com o uso de
extensômetros. O extensômetros elétricos propiciam medidas precisas das
deformações através do registro das variações da corrente elétrica (quando o
extensômetro se deforma, a resistência elétrica e, por conseguinte, a corrente
elétrica são alteradas).
A determinação do estado de tensão em um ponto (estado plano de tensões) pode
ser feita a partir de medidas de deformações com a utilização de rosetas de
deformação. Uma roseta de deformação é composta de um conjunto de
extensômetros elétricos dispostos em um dado plano e segundo direções
conhecidas.
Colando-se uma roseta com 3 extensômetros sobre a superfície de um elemento
estrutural faz-se a leitura das deformações lineares segundo estas 3 direções e
calcula-se as componentes do estado de deformações.
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
23
θc
θb
θa
x
Cálculo da deformação linear em uma dada direção θa:
[ ]
x
=
 xy
2
 xz
2
 xy
2
y
 yz
2
 xz
2
nx
 yz
⋅ ny
2
nz
z
{}
como se trata de um problema de estado plano de tensões,
 xy = xz =0 e, portanto,  xy = xz =0
assim,
[ ] {
x
 xy
2
 =  xy
2
0
y
0
0
{ }
x⋅cos a 
 xy
⋅sen  a
2
cos a
⋅ sen  a =  xy
0
⋅cos a  y sen a
0
2
0
z
}
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
24
{ }
cos a
 xy
 =x⋅cos a xy⋅sen  a ; ⋅cos  a y⋅sen a ; 0⋅ sen  a
2
0


2
2
 = x⋅cos a xy⋅sen a⋅cos a  xy⋅cos  a⋅sen a y sen a
2
2

2
2
 = x⋅cos a y sen a  xy⋅sen 2 a
2
a
a
a
analogamente para os ângulos θb e θc, vem

2
2
 = x⋅cos b y sen b  xy⋅sen 2b
2
b
2
2
 =x⋅cos  c y sen  c
c
 xy
⋅sen 2 c
2
Tem-se, assim, um sistema com 3 equações e 3 incógnitas, cuja solução oferece
como resultado os valores das componentes de deformação no plano (εx, εy e γxy).
Roseta 45° (são medidas as deformações ε0°, ε45° e ε90°)
90°
45°
0°
fazendo o eixo x na direção 0° e o eixo y na direção 90°,
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
25
x =0°
 y =90 °
2
45° = x⋅cos 45 ° y⋅sen ² 45° 
 xy
⋅sen 2⋅45° 
2
1
1 
45° = x⋅  y⋅  xy
2
2 2
 xy =2⋅45° −x  y 
Roseta 60° (são medidas as deformações ε0°, ε60° e ε120°)
120°
0°
60°
fazendo o eixo x na direção 0°
x =0°
 xy
1
3  3
⋅sen2⋅60 °= x⋅  y⋅  xy ⋅
2
4
4 2 2

1
3  − 3
120 °=x⋅cos2 120 °  y⋅sen ² 120 ° xy ⋅sen2⋅120 °= x⋅  y⋅  xy ⋅

2
4
4 2
2
2
60° = x⋅cos 60 ° y⋅sen ² 60 °
resolvendo o sistema de equações, vem:
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
26
 xy =
2
3
⋅60° −120 ° 

2
 y = ⋅60 °120 ° − 0 ° 
3
2
Conhecidas as componentes de deformação no plano xy e sabendo que se trata de
um estado plano de tensões (σz = 0, τxz = τyz = 0), pode-se determinar as
componentes do estado tensional e a componente de deformação perpendicular ao
plano xy (εz) utilizando a lei de Hooke generalizada.
x 
− ⋅
E E y
 
 y = y − ⋅ x
E E
−
z = ⋅ x  x 
E

 xy = xy
G
x =
multiplicando a expressão de εx por ν e somendo-a com a expressão de εy,
⋅x  y =
y
2
⋅1−  ,
E
E
E
⋅ y ⋅ x  e  x =
⋅x ⋅ y 
2
1−
1− 2
 xy =G .⋅ xy
 y=
substituindo os valores de σx e de σy na expressão de εz, vem
 E
z =− ⋅
⋅  ⋅1
E 1− ² x y
z =−

⋅x  y 
1−2
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
27
Energia Potencial de Deformação
No Estado Simples de Tensão, temos:
σx
σx
dy
- Força elementar resultante na direção x:
dF x = x⋅dA= x⋅dy⋅dz
dx
dz
dF
- Deslocamento correspondente:
d  x = x⋅dx
dUx
dFx
- Energia potencial acumulada no volume elementar:
 ⋅
1
1
dU x = ⋅dF x⋅d  x = ⋅ x⋅ x⋅dx.⋅dy⋅dz= x x⋅dV
2
2
2
dΔx
dΔ
No Estado Geral de Tensão (usando o PSE), temos:
1
dU = ⋅ x⋅x  y⋅ y  z⋅z  xy⋅ xy  yz⋅ yz zx⋅ zx ⋅dV
2
ou, usando a Lei de Hooke Generalizada,
dU
1
1
=
⋅[ 2x  2y  2z −2 ⋅ x⋅ y  y⋅ z  z⋅ x ] ⋅2xy 2yz 2zx  .
dV 2 E
2G
Em termos das tensões principais,
dU
1
=
⋅[ 12 22 23−2⋅ 1⋅ 2 2⋅ 3 3⋅ 1 ].
dV 2 E
Suponhamos cada estado de tensão como a superposição de dois outros estados
tais que:
σ
σ2
σ2'
σ3
σ1 =
σ1'
σ +
σ3'
σ
(1)
(2)
e que a variação do volume do estado (1) seja a mesma do estado resultante, isto
é, a variação do volume do estado (2) seja nula.
Assim, a deformação volumétrica do estado (2) é
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
28
εv’ = ε1’ + ε2’ + ε3’ = 0
⇒
(σ1’ + σ2’ + σ3’).(1 - 2ν) = 0
Como esta relação é válida para qualquer material (qualquer valor de ν),
σ1 ’ + σ2 ’ + σ3 ’ = 0
De acordo com a suposição acima,
σ1 = σ + σ1 ’
σ2 = σ + σ2 ’
σ3 = σ + σ3 ’
Somando as expressões acima membro a membro, temos:
σ1 + σ2 + σ3 = 3 σ + σ1 ’ + σ2 ’ + σ3 ’ = 3 σ
Daí, concluímos que as componentes dos estados (1) e (2) são:
 1 2 3
3
 1 ' = 1− ,
 2 ' = 2− e
 3 ' = 3− .
=
,
Como o estado (1) não realiza trabalho nos deslocamentos originados pelas forças
do estado (2) e vice-versa, podemos afirmar:
dU dU v dU d
=

dV
dV
dV
onde Uv é a energia de variação da volume e
Ud é a energia de variação da forma (energia de distorção)
Substituindo as componentes de tensão do estado (1) na expressão da energia de
deformação, temos:
dU v
1−2⋅
=3⋅ 2⋅
dV
2E
dU v
1−2⋅
= 1 2 32⋅
dV
6E
ou
ESTADOS DE TENSÃO E DE DEFORMAÇÃO
29
dU v
1−2⋅
= x  y  z 2⋅
dV
6E
dU v
1−2⋅
= I 12⋅
dV
6E
ou
onde I1 é o primeiro invariante de tensão.
dU d dU dU v
,
=
−
dV
dV dV
dU d
1
=[ 1− 2 2 2− 3 2 3− 1 2 ]⋅
dV
6E
ou
dU d
2xy 2yz 2zx 
2
2
2 1
=[ x − y   y − z   z − x  ]⋅

dV
6E
2G
Observação:
Para o estado simples de tensão, σ1 = σ, σ2 = σ3 = 0 (tração) ou σ1 = σ2 = 0, σ3 = σ
(compressão), temos
dU v
1−2⋅
= 2⋅
dV
6E
dU d
1
= 2⋅
dV
3E
e
dU dU v dU d  2 ⋅
.
=

=
=
dV
dV
dV 2 E
2
Para o estado de cisalhamento puro, σ1 = - σ3 = σ, σ2 = 0, temos:
dU v
=0
dV
e
dU d
1
.
= 2⋅
dV
E
Para o estado triaxial uniforme, σ1 = σ2 = σ3 = σ, temos:
dU v
1−2⋅
=3⋅ 2⋅
dV
2E
e
dU d
=0 .
dV
ESTADOS DE TENSÃO E DE DEFORMAÇÃO