TRANSFERÊNCIA DE CALOR POR CONVECÇÃO • Transferência

TRANSFERÊNCIA DE CALOR POR CONVECÇÃO
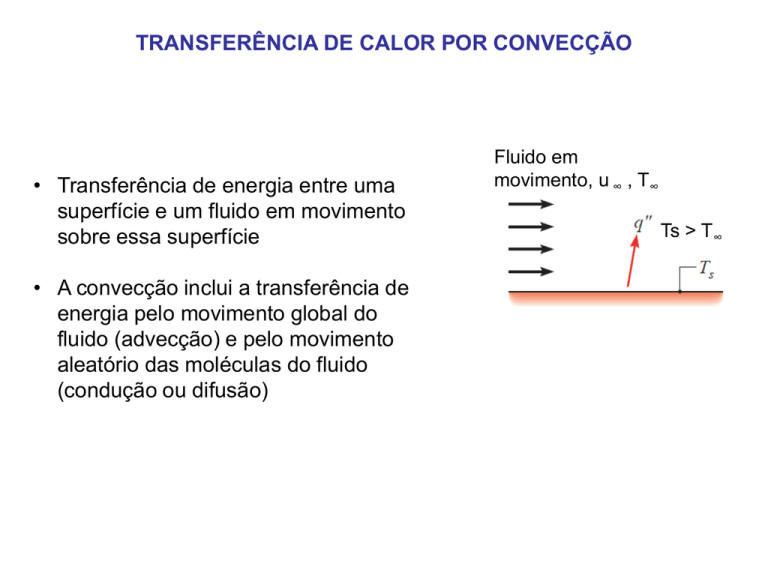
• Transferência de energia entre uma
superfície e um fluido em movimento
sobre essa superfície
• A convecção inclui a transferência de
energia pelo movimento global do
fluido (advecção) e pelo movimento
aleatório das moléculas do fluido
(condução ou difusão)
Fluido em
movimento, u ∞ , T∞
Ts > T∞
Forçada por meios externos:
ventilador, bomba ou vento
Forças de flutuação causadas por diferença
de densidade, devido à variação da
temperatura do fluido
Convecção com Mudança de fase – movimento induzido pelas
bolhas ou gotículas de líquido
Classificação dos escoamentos
Escoamentos VISCOSOS vs. INVÍSCIDOS
Escoamentos INTERNOS vs. EXTERNOS
Escoamentos COMPRESSÍVEIS vs. INCOMPRESSÍVEIS
Escoamentos LAMINARES vs. TURBULENTOS
Escoamentos NATURAIS (LIVRES) vs. FORÇADOS
Escoamentos PERMANENTES vs. TRANSIENTES
Escoamentos UNI, BI ou TRIDIMENSIONAIS
FATORES QUE INFLUENCIAM A CONVECÇÃO
Propriedades do fluido: massa específica, viscosidade, condutividade
térmica, calor específico
Propriedades do escoamento: velocidade (laminar, turbulento), temperatura
Geometria: escoamento externo, interno, rugosidade da superfície
 Massa específica kg/m³
 Viscosidade dinâmica Ns/m²
k Condutividade térmica W/m²K
Cp Calor específico J/kgK
 Viscosidade cinemática m²/s
 Difusividade térmica m²/s
Convecção – lei de resfriamento
TAXA DE CALOR (W)
FLUXO DE CALOR (W/m²)
CAMADA LIMITE DE VELOCIDADE
Região de escoamento afetada cinematicamente pela presença do corpo
Perfil de velocidade (ação viscosa)
Corrente livre

Camada
limite de
velocidade
-
Parede: condição de não-deslizamento
Corrente livre: escoamento irrotacional
(inviscido)
-
Aparecimento do perfil de velocidades:
origem da força de arraste
espessura da c.l.: valor
de y para u=0,99 u
Com aumento de x efeitos
de viscosidade penetram na
corrente livre e C.L.
aumenta (  aumenta com x)
- maneira na qual u varia com y através
da camada limite
- gradientes de velocidade e  são
consideráveis
C.L. de velocidade na mecânica dos fluidos: fornece a base para o cálculo do
coeficiente de atrito
Para escoamento externo
O gradiente de velocidade
na superfície depende da
distância x da aresta frontal
da placa
CAMADA LIMITE DE TÉRMICA
Corrente livre
t espessura da c.l.: valor de y
para:
Camada
limite térmica
(Ts-T)/(Ts-T∞) = 0,99
Com aumento de x efeitos da
transferência de calor
penetram na corrente livre e
C.L. aumenta ( t aumenta
com x)
Se desenvolve se houver diferença de temperatura entre a temperatura da
superfície, Ts, e a da corrente livre de fluido, T∞
Região do escoamento afetada termicamente pela presença do corpo
Parede: não deslizamento (condução pura)
Corrente livre: irrotacional (isotérmico)
Na camada limite: perfil de temperatura (condução + advecção), T = T(x, y)
A relação entre as condições na camada limite térmica e o coeficiente de
transferência de calor por convecção, h, pode ser demonstrada
Sobre a transferência de calor, a condição de não deslizamento (condução pura)
leva a:
Fluxo térmico na
superfície local
q"k
Lei de resfriamento
de Newton
q"c
=
q"k
h=
k
-
( Ts
∂T
T∞ ) ∂ y
∂T
=-k
∂y y = 0
q"c = h( Ts
-
T∞ )
∂T
∂y y =0
y =0
As condições na c.l.t. que influenciam o gradiente de temperatura na superfície
determinam a TC na através da camada
T/y|y=0 diminui com o aumento de x
q” e h diminuem
hlocal e hmédio
O fluxo térmico na superfície e o coeficiente de transferência de calor convectivo
variam ao longo da superfície
q=
∫
q" dAs
ou
q = ( Ts
-
∫
T∞ ) hdAs
As
As
q = h As ( Ts
-
T∞ )
1
h=
As
1 L
h=
hdx
L 0
∫
∫
As
hdAs
ESCOAMENTOS LAMINAR E TURBULENTO
Região
turbulenta
Camada de
amortecimento
Subcamada
viscosa
Turbulento
Laminar
Transição
Escoamento laminar: movimento altamente ordenado
Escoamento turbulento: altamente irregular e caótico, resulta em flutuações de velocidade e
de pressão
Subcamada viscosa: transporte dominado pela difusão, grandes gradientes de velocidade
Região turbulenta: transporte dominado pela mistura turbulenta, perfil de velocidades plano
 maiores na porção turbulenta da c.l. que na porção laminar
A turbulência afeta a espessura da C.L. e o perfil de velocidades
ESCOAMENTOS LAMINAR E TURBULENTO
A ocorrência de um regime laminar ou turbulento, e a transição entre eles, está
associada à relação entre as forças de inércia e viscosas no escoamento
Número de Reynolds, Re = Forças de inércia/ Forças viscosas
ρu 2 L2
Re =
μuL
ρu∞ L u∞ L
Re =
=
μ
ν
-
Re << as forças de inércia são insignificantes em relação às viscosas e os distúrbios
são dissipados e os escoamento permanece laminar
-
Re>> as forças de inércia são suficientes para amplificar os mecanismos de “gatilho” e
a transição para a turbulência ocorre.
Para escoamento sobre placa plana:
-
Recr

5 x10 5
A turbulência intensifica a transferência de calor, mas às custas de um aumento nas
perdas por atrito
Número de Nusselt, Nu
Parâmetro adimensional resultante a partir das definições do coeficiente
de transferência de calor
_
T
Ts
*
T = _
T∞ Ts
k
∂T
h= ( Ts _ T∞ ) ∂y
k (T∞ - Ts ) ∂T *
h=L (Ts - T∞ ) ∂y*
hL
∂T *
Nu =
=+ *
k
∂y
x
x =
L
*
y =0
y* = 0
y* = 0
e
k ∂T *
h=+
L ∂y*
y
y =
L
*
y* = 0
Parâmetro igual ao gradiente de
temperatura adimensional na
superfície e fornece uma medida da
transferência de calor por convecção
na superfície
hL
∂T *
Nu =
=+ *
k
∂y
y* = 0
Representa para a camada limite térmica o que o coeficiente de atrito representa para a
camada limite de velocidade
Nu = f ( x* , ReL , Pr)
A partir de Nu o h local pode ser determinado e o fluxo térmico local.
O coeficiente médio é obtido por integração ao longo da superfície e independente da
variável espacial x*
hL
Nu =
= f (ReL , Pr)
k
Equações da camada limite laminar
1. Equação da conservação da massa – equação da continuidade
- Bidimensional
- Coordenadas cartesianas x e y
- Fluido incompressível -  constante
-  massa específica
- u e  velocidades nas direções x e y
- W largura
- Coordenadas cilíndricas
2. Equação de momentum
3. Equação da conservação de energia
Energia térmica deixa o v.c.
devido ao movimento do fluido
(advecção)
Entrada líquida de
energia devido a
condução em y
Dissipação
viscosa